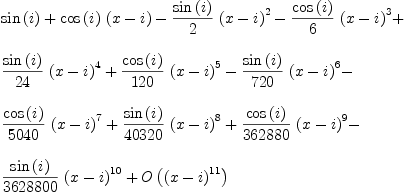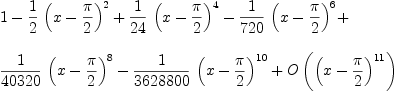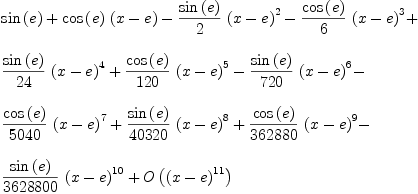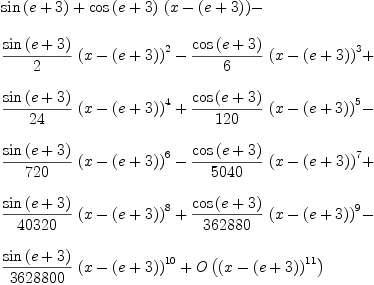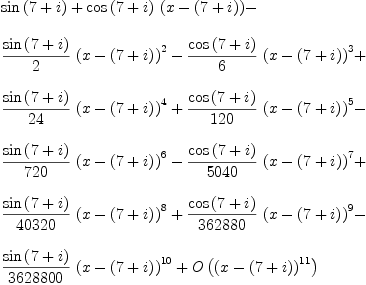Original Date: Sun, 13 Mar 2005 08:44:43 -0600 axiom series(sin(x),
Type: UnivariatePuiseuxSeries?(Expression Complex Integer,x,)
^^
but for Integer for example
Type: UnivariatePuiseuxSeries?(Expression Integer,x,0)
With binary infix operator in expansion point,
transform it to fortran (displayed type) -- Sun, 20 Mar 2005 14:33:53 -0600 reply axiom series(sin(x),
axiom series(sin(x),
axiom series(sin(x),
axiom series(sin(x),
file: format.boot.pamphlet Infix Binary Operator: "=" "+" "-" "" "/" "*" "^" (i-output.boot.pamphlet => function isBinaryInfix) function: form2String1 call fortexp0
%i\> .
It's not heavily tested but relatively simple (check it).
See above for details.
Severity: normal => critical
Bill, I think you can change the name of this issue. The problem concerns expansion point that involve binary operator too (for example 1+3*i).
Category: Axiom Compiler => Axiom Interpreter
Status: open => closed
|
|
|
|
last edited 9 years ago by test1 |