|
|
|
last edited 6 years ago by test1 |
Edit detail for #227 <code>random()$Integer</code> is a strange function revision 6 of 6
| 1 2 3 4 5 6 | ||
|
Editor: test1
Time: 2018/02/08 16:22:26 GMT+0 |
||
| Note: | ||
added:
From test1 Thu Feb 8 16:22:26 +0000 2018
From: test1
Date: Thu, 08 Feb 2018 16:22:26 +0000
Subject:
Message-ID: <20180208162226+0000@axiom-wiki.newsynthesis.org>
Status: fix proposed => closed
Currently there is a function random() for IntegerNumberSystem, which is documented to return a random number:
random : () -> %
++ random() creates a random element.
Of course, this is really a half-lie. There is no uniform distribution over the integers, so one wonders which distribution is used.
After a grep I found the definition for random()$INT in interp/spad.boot.pamphlet:
(defun |random| () (random (expt 2 26)))
So, at least the documentation should change. But in fact, I don't see why such a function should exist at all.
Martin
random() is a categorical specification and it is not possible to be more specific without knowing the domain. It is certainly useful in creating derived random functions that are more meaningful such as random(n) or random(m,n). It does not mean that n is limited to random()$INT shows uses in other domains (such as Float, Fraction Integer). There are many algorithms (like factoring integers) that use monte carlo methods.
Of course, one only implements pseudo-random numbers and not truely random numbers on computers (excluding quantum computers). But that is generally understood. Once restricted to a finite integer interval, uniform distribution makes sense even if it may only be programmed approximately.
It should be the responsibility of each domain to be specific on what random() exactly does and the algorithm used, but not at the category level. So for random()$INT, yes, the documentation should say the random number lies between 1 and ![]() . But that is not crucial since developers know that, and for users, there is
. But that is not crucial since developers know that, and for users, there is random(n)$INT for any n (also implemented in Lisp), which one should use instead in applications.
William
Using browse I found that random() is implemented only for three types:
QuotientFieldCategoryif hasIntegerNumberSystemIntegerNumberSystemFinite
I think the first two should go away, since, mathematically they make no sense. random() is not implemented for Float. In fact, I could not find a single affected operation! If you find one, could you please post it here? Caution: there are some domains, for example FSAGG that use random()$Integer, but only in the finite case. In fact, it appears to me that their use is mathematically wrong and should be replaced by random(n)$Integer.
Martin
You are right,random() is not implementd or specified in Float (it should!) and the above three categories are the only ones Hyperdoc shows. But random() for Float is available in almost any computation software and the lack of it in Axiom is simply because Axiom developers were hardly interested in floating point computations at the time. It surely does not imply that random()$Float has no applications (how about probability theory and statistics?) The neglect of numerical computation tools may be a fatal flaw in the development of Axiom, especially when it claims to be "the Scientific Computation System". So much so that even after hooking up with NAG's Fortran library and adding graphics, it was not able to attract the real scientific community and only the computer algebra community. With the convergence of symbolic-numerical computation as a dominating theme at ISSAC, it is crucial for the survival of Axiom to strength its numerical applications, and random number generation for floating point numbers is definitely a basic tool.
You seem to insist to interpret random()$INT to mean a random integer chosen out of all integers, and in this sense, then you are correct, but only because the implementation of random()$INT uses the Lisp version, not because it is inherently impossible to generate such a random integer (see Third point below). I think you cannot give a better documentation for this function for a category, and you cannot specify a function random(n) without knowing the domain where n lives or an explicit bijection between the set and some segment of integers. The function random() has meaning for any set, finite or not, and in the case the set is finite, it can be used without having to worry about the size of the set. Of course, in implementing such a function for a finite set, like the first line shown below (the result of grep), there is a tacit assumption that the size of the finite set is less than ![]() . We may consider that
. We may consider that ![]() is a system constant due to hardware or efficiency consideration (in fact, due to Lisp implementation) and should be documented. I would agree that in certain places, using random(n) is technically more correct since it would not subject the set to a system limit, but I don't follow your reasoning to remove it altogether. Of course, it is possible to remove any code, and rewrite it in some other form, but that would be both unnecessary and counter-productive. Here're my reasons.
is a system constant due to hardware or efficiency consideration (in fact, due to Lisp implementation) and should be documented. I would agree that in certain places, using random(n) is technically more correct since it would not subject the set to a system limit, but I don't follow your reasoning to remove it altogether. Of course, it is possible to remove any code, and rewrite it in some other form, but that would be both unnecessary and counter-productive. Here're my reasons.
Firstly, you cannot really start random(n)$INT without a seed (here n is NOT the seed but an upper bound for the range). Axiom uses random()$INT to provide the seed for its algebra codes (see line in d01agents.spad). Of course, random()$Lisp must have its own seed, possibly taken from some hardware clock. But random()$INT provides a higher level of conceptual abstraction for the seed and that is a valid design for algebra code.
Secondly, to remove random() means removing all the lines grepped below and hoping it will not break anything. Are you willing to spend the time to track this? Are you going to replace this with random(n) by forcing the usage to require knowing the size of a set a priori (consider the set of compositions of a positive integer k, for example) and knowing some hardware clock address? The version random()$S hides these technicalities from the user. Which version would be more user friendly? Unless you want to do away with random elements altogether, you will also have to set up explicit bijections, which is not possible for the generality Axiom is designed for.
Thirdly, it is not inconceivable to select random elements out of an infinite set. For example, take Streams over a finite set (say GF(2)). We can conceptually generate a random stream of binary digits and implement this as random()$Stream(GF(2)). We simply need to generate each digit randomly one at a time. (I will not argue with you whether such an stream of binary digits is truely random or not, since this is moot because we never finish doing so; and I know that if a pseudo-random generator is used to generate the coordinates of an n-dimension point, then these points lie on certain hyperplanes in n-dimensional space. These are simply properties of these pseudo-random generators, and do not invalidate the mathematical concept of a random element from an infinite set.) Now it is just a simple leap to consider these streams as integers expressed in binary, where the k-th bit is the bit for 2k. Since Axiom can compute (or at least simulate computing) with streams, Axiom can compute with random elements from the ring of integers.
Fourthly, which do you think is more efficient: to generate a random integer one bit at a time, and having to stop somewhere eventually, or to generate a random integer within a bound of 226?
In conclusion, I agree that one may use random(n)$INT almost everywhere random()$INT is used in the implementation of random()$S for a finite set S. I say "almost" because in defining the seed in algebra code, it is convenient to use random()$INT ; I say "may" rather than "should" because in many cases where usage is random()$INT modulo a small integer, the system bound is of no concerns. However, I don't think you can or should replace random()$S by random(n)$S since the latter need not make sense for some sets S (for example, where the concept of next or the bijection with 1..n is not given).
William
I disagree:
random()has meaning only if I specify a distribution. If no distribution is specified, usually the uniform distribution is taken. There is no uniform distribution on the integers, nor on the reals. By the way: random without an argument is not a lisp function!- I am not proposing to remove
random()for finite sets. If it is known how to select an element from a certain finite set - for example the set of partitions of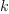 - then
it should be implemented. In fact: it is.
By the way: I don't see how knowing the size of a set helps with creating a random
element. I believe one needs some way of enumerating the elements?
Furthermore, I think that lines like
- then
it should be implemented. In fact: it is.
By the way: I don't see how knowing the size of a set helps with creating a random
element. I believe one needs some way of enumerating the elements?
Furthermore, I think that lines like random()$Z rem 11are a bad idea, since the resulting distribution will be nearly uniform, but not quite... Do you know why such code was written? - I did not say that it is impossible to create a random element of the integers
according to some distribution. Only: it cannot be the uniform distribution...
To generate random Integers according to a specific distribution we have
RIDIST.
Apart from the usage in D01AGNT - where random()$Integer is used to generate a seed, did you find any other places where random()$Integer is used?
Finally: Which CAS defines a function random for floats? I checked Mathematica and MuPAD?, the both define functions that return a (uniformly distributed) float between zero and one. This is reasonable, since most (all?) other distributions can be generated from that one.
Martin
random() has meaning only if I specify a distribution.
True (but that's a bit arrogant? :-). So the flaw is not in random(), but in the documentation because the distribution is not given. I never said that the random() for streams in my example is distributed uniformly. I am just saying that random() makes sense, indeed, better sense, for infinite sets and should not be removed.
I am not proposing to remove random() for finite sets.
Good. Are you proposing to remove it from infinite sets? or just IntegerNumberSystem and QuotientFieldCategory domains? If you are only objecting to the documentation, then I don't agree with removing a function because of documentation error.
By the way: I don't see how knowing the size of a set helps with creating a random element. I believe one needs some way of enumerating the elements?
An enumeration of a finite set means (at least implicitly) a bijection from 1..n (where n is the size) to the set, and then a call to random(n) can be used to index into an element of the set. The enumeration alone is not enough to generate a random element. On the other hand, I believe the size is necessary: even if one starts with a seed element of the set, any algorithm to generate the next random element (not just next element) from the current one most likely will need to know the size of the set to ensure a uniform distribution. I guess if someone is really clever, it is possible to have such an algorithm independent of the size and prove that every element has the same probability of being chosen. I don't have an example.
Finally: Which CAS defines a function random for floats?
That depends on what is meant. Floats are not the same as reals and a random float is not the same as a random real. Yes, random for floating point is usually done for the interval (0, 1) and then it can be scaled for any interval. So I don't see what we are disagreeing about. As you pointed out, Mathematica has Random[]. I am surprised that Maple does not. But it is easy to scale rand(), which "returns a random 12 digit non-negative integer" (I believe Maple meant less than or equal to 12 digit) to float.
By the way: random without an argument is not a lisp function!
Sure, random(n) is a Lisp function for positive integer n, and in boot, random() is defined in terms of it, precisely to abstract it for use with sets that are not related to the integers. But I suppose you don't agree that random() is a better calling convention for abstract data sets.
Apart from the usage in D01AGNT - whererandom()$Integeris used to generate a seed, did you find any other places whererandom()$Integeris used?
Sure, if you just look at the list I attached above last time.
But this is besides the point. Indeed, all such use can be replaced by random(2^26)$Lisp. I think you are missing the idea behind the deliberate creation of random() to enable the concept of random elements of an abstract data set and free this conceptually from the underlying intermediate languages (like Lisp) and machine hardware, as well as any implementation of random(n) for a random integer in the interval ![]() .
.
Furthermore, I think that lines like random()$Z rem 11 are a bad idea, since the resulting distribution will be nearly uniform, but not quite... Do you know why such code was written?
You are getting really picky here! The error (for nearly uniformity) when the size is small (like 11, as compared to ![]() ) is so small that I don't think it is significant. All numerical computation with floating points (and probabilities are certainly done in floating point in most scientific applications), approximation is used and here, the error in uniformity is no bigger than floating point error (this is itself only an approximate statement, I have not done the mathematical analysis!). Moreover, any statistical applications based on random samples are subject to sampling errors which are significantly (no pun intended) larger than rounding errors.
) is so small that I don't think it is significant. All numerical computation with floating points (and probabilities are certainly done in floating point in most scientific applications), approximation is used and here, the error in uniformity is no bigger than floating point error (this is itself only an approximate statement, I have not done the mathematical analysis!). Moreover, any statistical applications based on random samples are subject to sampling errors which are significantly (no pun intended) larger than rounding errors.
I think the code is a matter of convenience, the same way random() for floats is done (usually by scaling the integer interval ![]() to
to (0, 1)). It can be easily fixed: just use something like random(11*(2^26 exquo 11))$INT rem 11 instead. If you are picky on modulo 11, you should be just as picky for random floats in the interval (0,1). Well, I guess you are.
Unless you are thinking of applications in exact simulations for theoretical probability and statistics, I don't see any reasons to fix these minor problems. We all know pseudo-random number generators have their deficiencies but until some equally efficient but more mathematically precise methods are available, we have to live with it. Even when that day comes, all we need to do is to replace the Lisp version. (Along that thought, if the lisp version of random() uses a larger upper bound than ![]() , will you be satisfied? Perhaps the number
, will you be satisfied? Perhaps the number ![]() should be parametrized as a system constant and the documentation should mention this.)
should be parametrized as a system constant and the documentation should mention this.)
William
I am proposing to keeprandom() only for finite sets. In this case it should
return a random element uniformly chosen from all elements.
For infinite sets, we have - or should have - functions which chose a random element chosen according to the distribution, indicated by the function name. Of course, not all distributions make sense on all sets... But I'm certain that this can be worked out.
However, I meanwhile realize that it can be very difficult to create a random element according to the uniform distribution of some finite domain. This is indeed a severe obstacle. I do not know whether this applies to any domain currently in Axiom.
Since you think that I'm missing the point, here is an example: why don't we
define random()$INT to be always equal to ![]() ? Of course, it wouldn't
make much sense in practice, but it is indeed a random integer, with a rather
peculiar distribution maybe. I believe that such functions should not be used.
? Of course, it wouldn't
make much sense in practice, but it is indeed a random integer, with a rather
peculiar distribution maybe. I believe that such functions should not be used.
Furthermore, I think that lines likerandom()$Z rem 11are a bad idea, since the resulting distribution will be nearly uniform, but not quite... Do you know why such code was written?
You are getting really picky here!
Yes.
just use something like random(11*(2^26 exquo 11))$INT rem 11 instead.
But why wouldn't you use simply random(11)$INT?
Unless you are thinking of applications in exact simulations for theoretical probability and statistics,
Since I'm currently working in statistics and probability...
Martin
Since I'm currently working in statistics and probability...
In that case, I completely agree with you on exactness whenever possible (depending on the computation and distribution involved). But those situations are rare (may be limited to only some discrete random variable with a finite sample space like the Binomial r.v.) I wonder how one can create even a normally distrihbuted random variable. In simulation programs involving a continuous random variable, uniformly distributed floats and the inverse of the cumulative distribution function are involved. How can you do any exact computations with continuous variables if you have to solve for the inverse of the cdf? You will need exact reals, and then an exact method to solve cdf(x)=y, for any uniformly distributed random real number y over (0,1). Even for discrete variables like the Poission variable, you will have to use floats, or else you get into exact summations and their inverses.
But why wouldn't you use simply random(11)$INT ?
Because I was not thinking or was stupid or both!
Now that I believe I am thinking, using random(11)$INT simply passes the question to Lisp and if you are still picky, you should investigate how the Lisp function random(n) is coded. Is it some variation of the usual linear congruence method, but perhaps extended to arbitrary precision with a large base like ![]() to cover really large
to cover really large n. For small n, it would be modulo n in the same way: that is, the algorithm for random(11)$Lisp may be actually something like random1(seed)$Lisp rem 11 translated to Lisp where random1 (name is arbitrarily made up) is the Lisp random number generator for single precision (4 byte, for example) integers and seed is the seed or previously generated random single precision integer. If so, it would be only approximately uniform also.
For infinite sets, we have - or should have - functions which chose a random element chosen according to the distribution, indicated by the function name. Of course, not all distributions make sense on all sets... But I'm certain that this can be worked out.
The way to go would seem to be to create two new categories ProbabilityDensityFunctions (or ProbabilityDensityFunctionSpace) and RandomVariable, say RandomVariable(S:Set, d:ProbabilityDensityFunction) where S is the sample space, and x:=random() would mean x is a r.v. on S with probabillity density function d, and then create domains for these. The actual design, parameters, and specifications will need be more carefully thought out, say whether to use the cdf instead of the pdf (it seems cdf has lots of advantages as it is easy to recover the pdf by differentiation in many cases and cdf is continuous), and what are useful functions ( seed(x), nextRandom(x) come to mind, but operations on r.v. such as finding the pdf of joint distributions, are possible too). Then, if we were in Aldor, we can retroactively make IntegerNumberSystem a subcategory (In Axiom, we add a package). This would be a major project, since as you know, probability theory gets generalized into measure theory and so on.
I think worrying about the proper syntax of random() for an infinite sample space is the least of our (your?) problems :-)
William
partial "fix" in FriCAS. See also Waldek's mail:http://groups.google.at/group/fricas-devel/msg/4428e5ce37b80c45
http://fricas.svn.sourceforge.net/viewvc/fricas?view=rev&revision=172 Status: open => fix proposed Status: fix proposed => closed