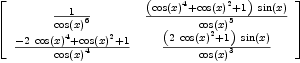It would be very nice if function simplify could operate on matrices, simplifying each element. use map --Bill Page, Sat, 12 Nov 2005 17:54:29 -0600 reply axiom A:=matrix _ [[tan(x)**6 + 3*tan(x)**4 + 3*tan(x)**2 + 1,
Type: Matrix(Expression(Integer))
axiom map(simplify,
Type: Matrix(Expression(Integer))
Status: open => closed
Category: New feature request => Axiom Library
|
|
|
|
last edited 16 years ago by kratt6 |
![\label{eq1}\left[
\begin{array}{cc}
{{{\tan \left({x}\right)}^6}+{3 \ {{\tan \left({x}\right)}^4}}+{3 \ {{\tan \left({x}\right)}^2}}+ 1}&{{{\tan \left({x}\right)}^5}+{3 \ {{\tan \left({x}\right)}^3}}+{3 \ {\tan \left({x}\right)}}}
\
{{{\tan \left({x}\right)}^4}+{3 \ {{\tan \left({x}\right)}^2}}}&{{{\tan \left({x}\right)}^3}+{3 \ {\tan \left({x}\right)}}}](images/8033162290931784648-16.0px.png "\label{eq1}\left[
\begin{array}{cc}
{{{\tan \left({x}\right)}^6}+{3 \ {{\tan \left({x}\right)}^4}}+{3 \ {{\tan \left({x}\right)}^2}}+ 1}&{{{\tan \left({x}\right)}^5}+{3 \ {{\tan \left({x}\right)}^3}}+{3 \ {\tan \left({x}\right)}}}
\
{{{\tan \left({x}\right)}^4}+{3 \ {{\tan \left({x}\right)}^2}}}&{{{\tan \left({x}\right)}^3}+{3 \ {\tan \left({x}\right)}}}")
![\label{eq2}\left[
\begin{array}{cc}
{1 \over{{\cos \left({x}\right)}^6}}&{{{\left({{\cos \left({x}\right)}^4}+{{\cos \left({x}\right)}^2}+ 1 \right)}\ {\sin \left({x}\right)}}\over{{\cos \left({x}\right)}^5}}
\
{{-{2 \ {{\cos \left({x}\right)}^4}}+{{\cos \left({x}\right)}^2}+ 1}\over{{\cos \left({x}\right)}^4}}&{{{\left({2 \ {{\cos \left({x}\right)}^2}}+ 1 \right)}\ {\sin \left({x}\right)}}\over{{\cos \left({x}\right)}^3}}](images/4277030502724341495-16.0px.png "\label{eq2}\left[
\begin{array}{cc}
{1 \over{{\cos \left({x}\right)}^6}}&{{{\left({{\cos \left({x}\right)}^4}+{{\cos \left({x}\right)}^2}+ 1 \right)}\ {\sin \left({x}\right)}}\over{{\cos \left({x}\right)}^5}}
\
{{-{2 \ {{\cos \left({x}\right)}^4}}+{{\cos \left({x}\right)}^2}+ 1}\over{{\cos \left({x}\right)}^4}}&{{{\left({2 \ {{\cos \left({x}\right)}^2}}+ 1 \right)}\ {\sin \left({x}\right)}}\over{{\cos \left({x}\right)}^3}}")