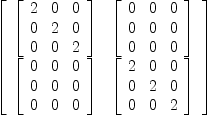
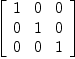Adding two square matrices of different dimension should result in an error. Axiom returns something that looks more like a tensor product.
The implementation of + for SquareMatrix? is inherited from Matrix (src/algebra/matrix.spad.pamphlet). Matrix inherits + from the default implementation in MatrixCategory? (src/algebra/matcat.spad.pamphlet).
There it says:
"+": (%,%) -> %
++ \spad{x + y} is the sum of the matrices x and y.
++ Error: if the dimensions are incompatible.
and is implemented
by default through:
x + y ==
((r := nrows x) ^= nrows y) or ((c := ncols x) ^= ncols y) =>
error "can't add matrices of different dimensions"
ans := new(r,c,0)
for i in minr(x)..maxr(x) repeat
for j in minc(x)..maxc(x) repeat
qsetelt_!(ans,i,j,qelt(x,i,j) + qelt(y,i,j))
ans
I have no idea why the following code returns something of type
SquareMatrix
?(2,SquareMatrix
?(3,Integer)).
fricas
)set message bottomup on
fricas
S d ==> SquareMatrix(d,Integer)
Type: Void
fricas
a2: S(2) := 1
Type: SquareMatrix
?(2,
Integer)
fricas
a3: S(3) := 1
Type: SquareMatrix
?(3,
Integer)
fricas
a2 + a3
Function Selection for +
Arguments: (SQMATRIX(2,INT),SQMATRIX(3,INT))
-> no appropriate + found in SquareMatrix(2,Integer)
-> no appropriate + found in SquareMatrix(3,Integer)
-> no appropriate + found in SquareMatrix(2,SquareMatrix(3,Integer))
-> no appropriate + found in SquareMatrix(2,Integer)
-> no appropriate + found in SquareMatrix(3,Integer)
[1] signature: (SQMATRIX(2,SQMATRIX(3,INT)),SQMATRIX(2,SQMATRIX(3,INT))) -> SQMATRIX(2,SQMATRIX(3,INT))
implemented: slot $$$ from SQMATRIX(2,SQMATRIX(3,INT))
Function Selection for map by coercion facility (map)
Arguments: ((INT -> SQMATRIX(3,INT)),SQMATRIX(2,INT))
Target type: SQMATRIX(2,SQMATRIX(3,INT))
-> no appropriate map found in SquareMatrix(2,Integer)
-> no appropriate map found in SquareMatrix(2,SquareMatrix(3,Integer))
-> no appropriate map found in SquareMatrix(3,Integer)
-> no appropriate map found in Integer
-> no appropriate map found in SquareMatrix(3,Integer)
Modemaps from Associated Packages
no modemaps
Remaining General Modemaps
[1] ((D3 -> D3),D) -> D from D
if D has XFALG(D2,D3) and D2 has ORDSET and D3 has RING
[2] ((D4 -> Union(D5,"failed")),Vector(D4)) -> Union(Vector(D5),
"failed")
from VectorFunctions2(D4,D5) if D4 has TYPE and D5 has TYPE
[3] ((D4 -> D5),Vector(D4)) -> Vector(D5) from VectorFunctions2(D4,
D5)
if D4 has TYPE and D5 has TYPE
[4] ((D4 -> D5),D3) -> D1
from UnivariateTaylorSeriesFunctions2(D4,D5,D3,D1)
if D4 has RING and D5 has RING and D1 has UTSCAT(D5) and D3
has UTSCAT(D4)
[5] ((D5 -> D6),UnivariatePuiseuxSeries(D5,D7,D9)) ->
UnivariatePuiseuxSeries(D6,D8,D1)
from UnivariatePuiseuxSeriesFunctions2(D5,D6,D7,D8,D9,D1)
if D5 has RING and D6 has RING and D7: SYMBOL and D9: D5
and D1: D6 and D8: SYMBOL
[6] ((D4 -> D5),D3) -> D1
from UnivariatePolynomialCategoryFunctions2(D4,D3,D5,D1)
if D4 has RING and D5 has RING and D1 has UPOLYC(D5) and D3
has UPOLYC(D4)
[7] ((D5 -> D7),UnivariatePolynomial(D4,D5)) -> UnivariatePolynomial
(D6,D7)
from UnivariatePolynomialFunctions2(D4,D5,D6,D7)
if D4: SYMBOL and D5 has RING and D7 has RING and D6:
SYMBOL
[8] ((D4 -> D5),UniversalSegment(D4)) -> Stream(D5)
from UniversalSegmentFunctions2(D4,D5)
if D4 has ORDRING and D4 has TYPE and D5 has TYPE
[9] ((D4 -> D5),UniversalSegment(D4)) -> UniversalSegment(D5)
from UniversalSegmentFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[10] ((D5 -> D6),UnivariateLaurentSeries(D5,D7,D9)) ->
UnivariateLaurentSeries(D6,D8,D1)
from UnivariateLaurentSeriesFunctions2(D5,D6,D7,D8,D9,D1)
if D5 has RING and D6 has RING and D7: SYMBOL and D9: D5
and D1: D6 and D8: SYMBOL
[11] ((D4 -> D5),SparseUnivariatePolynomial(D4)) ->
SparseUnivariatePolynomial(D5)
from SparseUnivariatePolynomialFunctions2(D4,D5)
if D4 has RING and D5 has RING
[12] ((D4 -> D5),Stream(D4)) -> Stream(D5) from StreamFunctions2(D4,
D5)
if D4 has TYPE and D5 has TYPE
[13] ((D4 -> D5),Sequence(D4)) -> Sequence(D5)
from SequenceFunctions2(D4,D5)
if D4 has COMRING and D5 has COMRING
[14] ((D3 -> D3),D) -> D1 from D
if D has SEGXCAT(D3,D1) and D3 has ORDRING and D1 has STAGG
(D3)
[15] ((D4 -> D5),SegmentBinding(D4)) -> SegmentBinding(D5)
from SegmentBindingFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[16] ((D4 -> D5),Segment(D4)) -> List(D5) from SegmentFunctions2(D4,
D5)
if D4 has ORDRING and D4 has TYPE and D5 has TYPE
[17] ((D4 -> D5),Segment(D4)) -> Segment(D5) from SegmentFunctions2(
D4,D5)
if D4 has TYPE and D5 has TYPE
[18] ((D9 -> D1),D6) -> D4
from RectangularMatrixCategoryFunctions2(D7,D8,D9,D10,D11,
D6,D1,D2,D3,D4)
if D9 has Join(SRNG,ABELMON) and D1 has Join(SRNG,ABELMON)
and D7: NNI and D8: NNI and D10 has DIRPCAT(D8,D9) and D11
has DIRPCAT(D7,D9) and D4 has RMATCAT(D7,D8,D1,D2,D3) and
D6 has RMATCAT(D7,D8,D9,D10,D11) and D2 has DIRPCAT(D8,D1)
and D3 has DIRPCAT(D7,D1)
[19] ((D4 -> D4),D) -> D from D
if D has RMATCAT(D2,D3,D4,D5,D6) and D4 has Join(SRNG,
ABELMON) and D5 has DIRPCAT(D3,D4) and D6 has DIRPCAT(D2,D4
)
[20] ((D4 -> D5),D3) -> D1 from QuaternionCategoryFunctions2(D3,D4,
D1,D5)
if D4 has COMRING and D5 has COMRING and D1 has QUATCAT(D5)
and D3 has QUATCAT(D4)
[21] ((D4 -> D5),D3) -> D1 from QuotientFieldCategoryFunctions2(D4,
D5,D3,D1)
if D4 has INTDOM and D5 has INTDOM and D1 has QFCAT(D5) and
D3 has QFCAT(D4)
[22] ((D4 -> D5),Point(D4)) -> Point(D5) from PointFunctions2(D4,D5)
if D4 has RING and D5 has RING
[23] ((D4 -> D5),PrimitiveArray(D4)) -> PrimitiveArray(D5)
from PrimitiveArrayFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[24] ((D4 -> D5),Polynomial(D4)) -> Polynomial(D5)
from PolynomialFunctions2(D4,D5)
if D4 has RING and D5 has RING
[25] ((D4 -> D5),Pattern(D4)) -> Pattern(D5) from PatternFunctions2(
D4,D5)
if D4 has SETCAT and D5 has SETCAT
[26] ((D5 -> D6),PatternMatchResult(D4,D5)) -> PatternMatchResult(D4
,D6)
from PatternMatchResultFunctions2(D4,D5,D6)
if D4 has SETCAT and D5 has SETCAT and D6 has SETCAT
[27] ((D4 -> D5),ParametricSurface(D4)) -> ParametricSurface(D5)
from ParametricSurfaceFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[28] ((D4 -> D5),ParametricSpaceCurve(D4)) -> ParametricSpaceCurve(
D5)
from ParametricSpaceCurveFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[29] ((D4 -> D5),ParametricPlaneCurve(D4)) -> ParametricPlaneCurve(
D5)
from ParametricPlaneCurveFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[30] ((D4 -> D5),OrderedCompletion(D4)) -> OrderedCompletion(D5)
from OrderedCompletionFunctions2(D4,D5)
if D4 has SETCAT and D5 has SETCAT
[31] ((D4 -> D5),OnePointCompletion(D4)) -> OnePointCompletion(D5)
from OnePointCompletionFunctions2(D4,D5)
if D4 has SETCAT and D5 has SETCAT
[32] ((D4 -> D5),D3) -> D1 from OctonionCategoryFunctions2(D3,D4,D1,
D5)
if D4 has COMRING and D5 has COMRING and D1 has OC(D5) and
D3 has OC(D4)
[33] ((D4 -> D5),MonoidRing(D4,D6)) -> MonoidRing(D5,D6)
from MonoidRingFunctions2(D4,D5,D6)
if D4 has RING and D5 has RING and D6 has MONOID
[34] ((D2 -> D2),D) -> D from D
if D has MRCAT(D2,D3) and D2 has RING and D3 has MONOID
[35] ((D7 -> D8),D3) -> D1 from MPolyCatFunctions2(D4,D5,D6,D7,D8,D3
,D1)
if D7 has RING and D8 has RING and D4 has ORDSET and D5 has
OAMONS and D1 has POLYCAT(D8,D6,D4) and D6 has OAMONS and
D3 has POLYCAT(D7,D5,D4)
[36] ((D5 -> Union(D8,"failed")),D4) -> Union(D2,"failed")
from MatrixCategoryFunctions2(D5,D6,D7,D4,D8,D9,D1,D2)
if D5 has Join(SRNG,ABELMON) and D8 has Join(SRNG,ABELMON)
and D6 has FLAGG(D5) and D7 has FLAGG(D5) and D2 has MATCAT
(D8,D9,D1) and D4 has MATCAT(D5,D6,D7) and D9 has FLAGG(D8)
and D1 has FLAGG(D8)
[37] ((D5 -> D8),D4) -> D2
from MatrixCategoryFunctions2(D5,D6,D7,D4,D8,D9,D1,D2)
if D5 has Join(SRNG,ABELMON) and D8 has Join(SRNG,ABELMON)
and D6 has FLAGG(D5) and D7 has FLAGG(D5) and D2 has MATCAT
(D8,D9,D1) and D4 has MATCAT(D5,D6,D7) and D9 has FLAGG(D8)
and D1 has FLAGG(D8)
[38] ((D4 -> D5),List(D4)) -> List(D5) from ListFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[39] ((D2 -> D2),InfiniteTuple(D2)) -> InfiniteTuple(D2)
from InfiniteTuple(D2) if D2 has TYPE
[40] ((D4 -> D5),InfiniteTuple(D4)) -> InfiniteTuple(D5)
from InfiniteTupleFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[41] ((D4 -> D5),Union(Record(mainpart: D4,limitedlogs: List(Record(
coeff: D4,logand: D4))),"failed")) -> Union(Record(mainpart: D5,
limitedlogs: List(Record(coeff: D5,logand: D5))),"failed")
from IntegrationResultFunctions2(D4,D5)
if D4 has FIELD and D5 has FIELD
[42] ((D4 -> D1),Union(D4,"failed")) -> Union(D1,"failed")
from IntegrationResultFunctions2(D4,D1)
if D4 has FIELD and D1 has FIELD
[43] ((D4 -> D5),Union(Record(ratpart: D4,coeff: D4),"failed")) ->
Union(Record(ratpart: D5,coeff: D5),"failed")
from IntegrationResultFunctions2(D4,D5)
if D4 has FIELD and D5 has FIELD
[44] ((D4 -> D5),IntegrationResult(D4)) -> IntegrationResult(D5)
from IntegrationResultFunctions2(D4,D5)
if D4 has FIELD and D5 has FIELD
[45] ((D2 -> D2),D) -> D from D
if D has IDPC(D2,D3) and D2 has SETCAT and D3 has COMPAR
[46] ((D2 -> D2),D) -> D from D if D has HOAGG(D2) and D2 has TYPE
[47] ((D4 -> D5),D3) -> D1 from FiniteSetAggregateFunctions2(D4,D3,
D5,D1)
if D4 has SETCAT and D5 has SETCAT and D1 has FSAGG(D5) and
D3 has FSAGG(D4)
[48] ((D4 -> D5),D3) -> D1 from FunctionSpaceFunctions2(D4,D3,D5,D1)
if D4 has Join(RING,COMPAR) and D5 has Join(RING,COMPAR)
and D1 has FS(D5) and D3 has FS(D4)
[49] ((D4 -> D5),D3) -> D1
from FramedNonAssociativeAlgebraFunctions2(D3,D4,D1,D5)
if D4 has COMRING and D5 has COMRING and D1 has FRNAALG(D5)
and D3 has FRNAALG(D4)
[50] ((D7 -> D11),FractionalIdeal(D7,D8,D9,D10)) -> FractionalIdeal(
D11,D1,D2,D3)
from FractionalIdealFunctions2(D7,D8,D9,D10,D11,D1,D2,D3)
if D7 has EUCDOM and D8 has QFCAT(D7) and D9 has UPOLYC(D8)
and D10 has Join(FRAMALG(D8,D9),RETRACT(D8)) and D11 has
EUCDOM and D1 has QFCAT(D11) and D2 has UPOLYC(D1) and D3
has Join(FRAMALG(D1,D2),RETRACT(D1))
[51] ((D4 -> D5),Fraction(D4)) -> Fraction(D5)
from FractionFunctions2(D4,D5)
if D4 has INTDOM and D5 has INTDOM
[52] ((D4 -> D5),Factored(D4)) -> Factored(D5)
from FactoredFunctions2(D4,D5)
if D4 has INTDOM and D5 has INTDOM
[53] ((D2 -> D2),Factored(D2)) -> Factored(D2) from Factored(D2)
if D2 has INTDOM
[54] ((D4 -> D5),D3) -> D1 from FiniteLinearAggregateFunctions2(D4,
D3,D5,D1)
if D4 has TYPE and D5 has TYPE and D1 has FLAGG(D5) and D3
has FLAGG(D4)
[55] ((D5 -> D8),D4) -> D2
from FunctionFieldCategoryFunctions2(D5,D6,D7,D4,D8,D9,D1,
D2)
if D5 has UFD and D8 has UFD and D6 has UPOLYC(D5) and D7
has UPOLYC(FRAC(D6)) and D9 has UPOLYC(D8) and D2 has FFCAT
(D8,D9,D1) and D4 has FFCAT(D5,D6,D7) and D1 has UPOLYC(
FRAC(D9))
[56] ((D2 -> D2),D) -> D from D if D has FEVALAB(D2) and D2 has
SETCAT
[57] ((D7 -> D11),FiniteDivisor(D7,D8,D9,D10)) -> FiniteDivisor(D11,
D1,D2,D3)
from FiniteDivisorFunctions2(D7,D8,D9,D10,D11,D1,D2,D3)
if D7 has FIELD and D8 has UPOLYC(D7) and D9 has UPOLYC(
FRAC(D8)) and D10 has FFCAT(D7,D8,D9) and D11 has FIELD and
D1 has UPOLYC(D11) and D2 has UPOLYC(FRAC(D1)) and D3 has
FFCAT(D11,D1,D2)
[58] ((D4 -> D5),Expression(D4)) -> Expression(D5)
from ExpressionFunctions2(D4,D5)
if D4 has COMPAR and D5 has COMPAR
[59] ((D4 -> D1),Kernel(D4)) -> D1 from ExpressionSpaceFunctions2(D4
,D1)
if D4 has ES and D1 has ES
[60] ((D -> D),Kernel(D)) -> D from D if D has ES
[61] ((D4 -> D5),Equation(D4)) -> Equation(D5)
from EquationFunctions2(D4,D5) if D4 has TYPE and D5 has
TYPE
[62] ((D2 -> D2),Equation(D2)) -> Equation(D2) from Equation(D2)
if D2 has TYPE
[63] ((D5 -> D6),DirectProduct(D4,D5)) -> DirectProduct(D4,D6)
from DirectProductFunctions2(D4,D5,D6)
if D4: NNI and D5 has TYPE and D6 has TYPE
[64] ((D4 -> D5),Complex(D4)) -> Complex(D5) from ComplexFunctions2(
D4,D5)
if D4 has COMRING and D5 has COMRING
[65] ((D6 -> D7),CartesianTensor(D4,D5,D6)) -> CartesianTensor(D4,D5
,D7)
from CartesianTensorFunctions2(D4,D5,D6,D7)
if D4: INT and D5: NNI and D6 has COMRING and D7 has
COMRING
[66] ((D4 -> D5),OneDimensionalArray(D4)) -> OneDimensionalArray(D5)
from OneDimensionalArrayFunctions2(D4,D5)
if D4 has TYPE and D5 has TYPE
[67] ((D2 -> D2),D) -> D from D
if D has ARR2CAT(D2,D3,D4) and D2 has TYPE and D3 has FLAGG
(D2) and D4 has FLAGG(D2)
[68] ((D2 -> D2),D) -> D from D
if D has AMR(D2,D3) and D2 has Join(SRNG,ABELMON) and D3
has OAMON
[1] signature: ((INT -> SQMATRIX(3,INT)),SQMATRIX(2,INT)) -> SQMATRIX(2,SQMATRIX(3,INT))
implemented: slot (SquareMatrix 2 (SquareMatrix 3 (Integer)))(Mapping (SquareMatrix 3 (Integer)) (Integer))(SquareMatrix 2 (Integer)) from RMCAT2(2,2,INT,DIRPROD(2,INT),DIRPROD(2,INT),SQMATRIX(2,INT),SQMATRIX(3,INT),DIRPROD(2,SQMATRIX(3,INT)),DIRPROD(2,SQMATRIX(3,INT)),SQMATRIX(2,SQMATRIX(3,INT)))
Type: SquareMatrix
?(2,
SquareMatrix
?(3,
Integer))
It seems the Axiom interpreter is trying really hard to
figure out what you might mean by this sum! The
bottomup
output shows the "mode selection" that it eventually arrives
at.
I don't know whether I should consider that
behaviour of Axiom as a bug or a feature.
If one puts
macro S d == SquareMatrix(d,Integer)
abc(): OutputForm ==
a2: S(2) := 1
a3: S(3) := 1
(a2 + a3)::OutputForm
into a file aaa.input and then says
)read aaa
abc()
one gets exactly the same result of type SquareMatrix
?(2,SquareMatrix
?(3,Integer)) as above.
Clearly, the same code, when put into aaa.spad does not even compile via
)co aaa
The danger is the following (which is maybe not clearly demonstrated by the code above):
If somebody writes some prototype of a function into an .input file and later wants to transform the code into a .spad form, s/he cannot expect that the result is the same. If the code does compile the semantics is still different since for the .input part the interpreter might add some knowledge.
That problem is certainly known to people who have used Axiom extensively, but it will come as a surprise if one is relatively new to Axiom.
Category: Axiom Library => Axiom Interpreter
Status: open => closed
It is true that Axioms interpreter and compiler apply (slightly) different semantics. However, it seems to me that if code compiles with spad, then it should return the same result when interpreted.
I'm quite sure that this problem is inevitable given that we want the interpreter to guess types...
Martin
I agree with Martin that we should expect that (most) SPAD functions
will work when written as function definitions in the Axiom interpreter
but usually not the other way around. Although the distinction between
interpreter and compiler is a bit ambiguous because functions are usually
also compiled to lisp in the Axiom interpret, where possible. The Axiom
interpreter however makes assumptions about types, performs "mode matching"
and does automatic coercions in an attempt to releave the user of having
to specify such details. This is not part of SPAD or Aldor semantics.
This "mode matching" mechanism in the Axiom interpreter is what gives
the perhaps unexpected result above. I think it goes something like
this: In trying to resolve the meaning of the + operator, mode
matching searches for coercions of the operands such that the signature
of some known (exposed) function matches the resulting signatures of
the operands and the type of the desired result (if specified). It
then applies the coercions and function of the first match it finds.
I think this behaviour is fundamental to the design of the Axiom
interpreter and cannot/should not be changed. However in a sense it
is/was only an experiment. There does not seem to be any sound and
complete theory of how it should work in practice. (I think there
is a paper about the theory of automatic coercions in the
reference library )
In particular, it is difficult to predict in
advance the affect for providing the interpret with certain coercion
paths since the mode matching search can become quite complex -
as the example above illustrates. But it is also essential for basic
use of the interpreter such as:
fricas
x+1
Function Selection for +
Arguments: (VARIABLE(x),PI)
-> no appropriate + found in Variable(x)
-> no appropriate + found in PositiveInteger
-> no appropriate + found in Symbol
-> no appropriate + found in Integer
-> no appropriate + found in Polynomial(Integer)
-> no appropriate + found in Variable(x)
-> no appropriate + found in PositiveInteger
-> no appropriate + found in Symbol
-> no appropriate + found in Integer
[1] signature: (POLY(INT),POLY(INT)) -> POLY(INT)
implemented: slot $$$ from POLY(INT)
Type: Polynomial(Integer)
where we see the interpreter does behave in a simple and expected
manner.
So in short: I think we need a theory, and then we need to review
and edit Axiom's current system of coercions to try to ensure that
the Axiom interpreter's behaviour is more intuitive for new users.
As an interim measure, it might be nice if we had a more user-friendly
way to display the results of the mode matching than the obscure
result of )set message bottomup on.