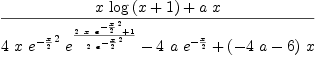The following input causes infinite recursion in rischNormalize fricas (1) -> integrate(simplify(D((log((x)+1)+a)/(2*((((x*(exp(exp(x)/2)))-(a*(x+exp(-x/2))))*(2/x))-3)),
Type: Union(Expression(Integer),
AFAICS goodCoef chooses to rewrite simpler kernel in terms of a more complex one. More precisely, rischNormalize is supposed to eliminate kernels which are algebraically dependent on other kernels. If a dependent kernel is found rischNormalize should eliminate it and recurse. So the recursion depth is limited by the number of kernels. However, in this example rischNormalize eliminates simpler kernel, but causes new kernels to appear. elementary integration really should be one of the strengths... --kratt6, Sat, 03 Jun 2006 07:52:55 -0500 reply Category: Aldor Library Compiler => Axiom Library
Severity: normal => serious
Status: open => fix proposed
Status: fix proposed => fixed somewhere
no patch available http://axiom.svn.sourceforge.net/viewvc/axiom/branches/wh-sandbox/src/algebra/efstruc.spad.pamphlet?r1=263&r2=377 Status: fixed somewhere => fix proposed Status: fix proposed => closed |
|
|
|
last edited 6 years ago by test1 |