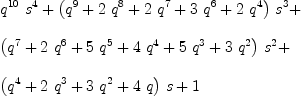The following is a very surprising for a novice, and a bit surprising for me:

c 0==1; c 1==1; c n==c(n-1)+s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..n-1]));

c 5

Compiling function c with type Integer -> Fraction(Polynomial(
      Integer))

(1)

Note that the type of c 5 is FRAC POLY INT. This is, because Axiom is not smart enough to realize inside the loop that 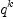is a polynomial if 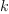is nonnegative. The following is more surprising, though:

coefficient(univariate(c(5),s),3)

(2)

Axiom manages - after a lot of trying- to coerce univariate(c(5),s) to a SUP FRAC POLY INT. Wow.

[coefficient(univariate(c(n),s),1) for n in 0..4]

   There are 8 exposed and 6 unexposed library operations named 
      coefficient having 2 argument(s) but none was determined to be 
      applicable. Use HyperDoc Browse, or issue
                           )display op coefficient
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.
   Cannot find a definition or applicable library operation named 
      coefficient with argument type(s) 
     Fraction(SparseUnivariatePolynomial(Fraction(Polynomial(Integer))))
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are 8 exposed and 6 unexposed library operations named 
      coefficient having 2 argument(s) but none was determined to be 
      applicable. Use HyperDoc Browse, or issue
                           )display op coefficient
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      coefficient with argument type(s) 
     Fraction(SparseUnivariatePolynomial(Fraction(Polynomial(Integer))))
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

But why does it give up here?

Martin

univariate applied to rational function produces rational function. Given actual value Axiom/FriCAS can see that rational function is a polynomial and retract it. But in a loop FriCAS has only expression producing rational functions and can not predict that the result will be a polynomial.

Zq:=SUP(INT)

(3)

q:Zq := monomial(1,1)

   Compiled code for c has been cleared.

(4)

Zqs:=SUP(Zq)

(5)

s:Zqs := monomial(1$Zq,1)

(6)

macro mac(n) == c(n-1) + s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..n-1]))

c(n: Integer): Zqs == (n=0 or n=1 => 1; mac n)

   Function declaration c : Integer -> SparseUnivariatePolynomial(
      SparseUnivariatePolynomial(Integer)) has been added to workspace.
   1 old definition(s) deleted for function or rule c

c 0

Compiling function c with type Integer -> SparseUnivariatePolynomial
      (SparseUnivariatePolynomial(Integer))

(7)

c 1

(8)

c 2

(9)

mac 2

(10)

I don't know but the output of c(2) is wrong. I would have expected "? ? + 1" in accordance to mac(2). So the typed form of you example doesn't work. And the output looks ugly anyway. :-(

Ralf

Here I even don't define the type of the function:

)clear all

   All user variables and function definitions have been cleared.
c 0==1; c 1==1; c n==c(n-1)+s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..(n-1)::NNI]));

[coefficient(univariate(c(n),s),1) for n in 0..4]

Compiling function c with type Integer -> Polynomial(Integer)

(11)

I don't know why it gives up in your exemple though.

Greg