Is the following a case of total simplification failure (a certain
bug from the user's point... unless AXIOM is not targeted for
Martians who as known have no need in simplification whatsoever :)
or
it is still possible to get %pi out of the lengthy expression
axiom
%i*log(-%i) - %i*log(%i)
Type: Expression(Complex(Integer))
?
Given my previous posting about complexForm, I mean maybe just a way
to expel those nasty logarithms and see the real and imaginary parts
not intertwined rather than a correct answer.
Any, maybe even a very cumbersome way?
.....................................................................
axiom
simplify(%i*log(-%i) - %i*log(%i))
Type: Expression(Complex(Integer))
axiom
normalize(%i*log(-%i) - %i*log(%i))
Type: Expression(Complex(Integer))
axiom
complexNormalize(%i*log(-%i) - %i*log(%i))
Type: Expression(Complex(Integer))
.....................................................................
COMPARE:
Derive 6.1> LOG(#i) - LOG(-#i) gives #i*pi
Maple 9.5.2> ln(I) - ln(-I); gives I*Pi
MuPAD 3.1> ln(I) - ln(-I); gives I*PI
Mathematica 5.1> Log[I] - Log[-I] gives I*Pi
Maxima 5.9.1> RECTFORM(LOG(%I) - LOG(-%I)); gives %I %PI
However:
AXIOM -> complexForm(log(%i) - log(-%i)) gives 0
The problem is in the operation "argument":
axiom
argument(%i)
Type: Expression(Integer)
axiom
argument(-%i)
Type: Expression(Integer)
the latter should be -pi/2, of course. The problem is in gaussian.spad,
COMPCAT:
if R has TranscendentalFunctionCategory then
half := recip(2::R)::R
if R has RealNumberSystem then
atan2loc(y: R, x: R): R ==
pi1 := pi()$R
pi2 := pi1 * half
x = 0 => if y >= 0 then pi2 else -pi2
-- Atan in (-pi/2,pi/2]
theta := atan(y * recip(x)::R)
while theta <= -pi2 repeat theta := theta + pi1
while theta > pi2 repeat theta := theta - pi1
x >= 0 => theta -- I or IV
if y >= 0 then
theta + pi1 -- II
else
theta - pi1 -- III
argument x == atan2loc(imag x, real x)
else
-- Not ordered so dictate two quadrants
argument x ==
zero? real x => pi()$R * half
atan(imag(x) * recip(real x)::R)
so the problem occurs if R does not have "RealNumberSystem?":
axiom
argument(-%i*1.0)
Type: Float
since Float does have RNS, but INT does not. I'm not quite sure what the
condition should be. OrderedSet?
OrderedRing, probably.
OrderedSet, wouldn't make sense...
Martin
Status: open => fix proposed
Severity: normal => critical
Hm, replacing
RealNumberSystem with
OrderedRing does not really work, since
EXPR INT does not have
OrderedRing... Furthermore,
FRAC INT does not have
TRAFUN... On the other hand, asking for
TranscendentalFunctionCategory also seems a lot, since only division by two is required.
Questions:
- Should
EXPR INT have OrderedRing ?
- Is
TRAFUN really necessary?
From: wyscc Thurs Jul 14 15:30:00 -5:00
On the other hand, asking for TranscendentalFunctionCategory also seems a lot, since only division by two is required.
Looking at the code above, to define argument in COMPCAT R, it seems we need, other than arithmetic in RING, the following:
R has OrderedSet
atan: % -> %
zero?: R -> Boolean
recip: % -> Union(%,"failed")
pi: () -> R
axiom
myhalf: ()-> EXPR INT
Type: Void
axiom
myhalf()==recip(2::EXPR INT)::EXPR INT
Type: Void
axiom
myArgument: Complex EXPR INT -> EXPR INT
Type: Void
axiom
myArgument(x) ==
zero? real x =>
imag(x) > 0 => pi()$(EXPR INT) * myhalf()
imag(x) < 0 => - pi()$(EXPR INT) * myhalf()
error "myArgument not defined at (0,0)"
atan(imag(x)*recip(real(x)))
Type: Void
axiom
myArgument(-%i)
There are 4 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
NonNegativeInteger
Expression(Integer)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
axiom
Compiling function myArgument with type Complex(Expression(Integer))
-> Expression(Integer)axiom
Compiling function myhalf with type () -> Expression(Integer)
Type: Expression(Integer)
axiom
myArgument(%i)
Type: Expression(Integer)
axiom
myArgument(3+5*%i)
Type: Expression(Integer)
axiom
myArgument(3-5*%i)
Type: Expression(Integer)
axiom
myArgument(0::Complex EXPR INT)
Error signalled from user code:
myArgument not defined at (0,0)
Note, I think the current returns by argument(0::Complex EXPR INT) and argument(0::Complex INT) as %pi/2 are wrong.
axiom
argument(0::Complex INT)
>> Error detected within library code:
(1 . failed) cannot be coerced to mode (Expression (Integer))
* Should EXPR INT have OrderedRing ?
Even POLY INT does not have OrderedRing and the reason given was to allow EXPR to implement abs. I thought about this briefly and wonder what abs of a polynomial really should be and find no satisfactory answer (one possibility is to define it relative to a term-ordering as the abs of the leading coefficient). You probably noted that OrderedRing is not the same as Join(OrderedSet, Ring). One use of ORDRING is to step through a segment. Clearly, there is no canonical meaning to stepping from one expression (or polynomial) to another (since some term-orderings like pure lex is not sequential because there may be infinitely many monomials between two).
* Is TRAFUN really necessary?
You meant TRANFUN? (Maybe it's not since searching hyperdoc with *TRANFUN* under constructors only returns FortranFunctionCategory :-). Seriously, I believe the reason is, like any other categories in Axiom, to allow multiple domains in the category (say due to the different data-representations or algorithms, or whether one wants symbolic computation or numerical), but to also provide a few default implementations valid across all domains of the category (unless overridden for some more efficient implementations).
In Axiom, it is easy (and we are sometimes forced) to spin out these hierarchical categories and domains of abstractions. In any other system, such abstractions are not really necessary because the author usually dictates every choice (notation, algorithm, input, output conventions). I once worked with a bright undergraduate student on developing something intended to be partial differential polynomial ring (where derivations are abstract operators, not necessarily the d/dx type) and wanted a flexible way to input/output partial differential algebraic equations (something rather simple?) and the number of categories and domains simply proliferated. One of the main hurdles is ordering the pieces (a general multivariate partial differential monomial carries a lot of data and notation). The student quitted, unfortunately leaving no notes of our numerous discussions on the design. I wonder whether MB worked alone on the design for transcendental functions or wrote notes to himself at least.
William
The proposed definition
myArgument is still not correct:
axiom
myArgument(-1+%i)
There are 4 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
NonNegativeInteger
Expression(Integer)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
axiom
Compiling function myArgument with type Complex(Expression(Integer))
-> Expression(Integer)Type: Expression(Integer)
but should be 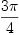 . We cannot get around the ordering of the ring involved... Of course, as soon as variables are involved, we cannot know anymore in which quadrant we are. So in this case we really should return
. We cannot get around the ordering of the ring involved... Of course, as soon as variables are involved, we cannot know anymore in which quadrant we are. So in this case we really should return argument unevaluated. This would probably involve making it an operator. A different possibility would be to introduce a new two argument operator atan paralleling the one in Float and DoubleFloat.
Martin
Martin:
Thanks for pointing out my error. In coding myArgument, I was not aiming for a general definition. I was experimenting to see if there is need for RealNumberSystem or OrderedRing.
As you proposed, it seems the error in myArgument may be fixed by a two argument version of atan (which only exists for Float and DoubleFloat currently). The usual sign convention will take care of the case of inputs involving variables. But I am not convinced one way or the other that OrderedRing is needed.
axiom
myhalf: ()-> EXPR INT
Compiled code for myhalf has been cleared.
Compiled code for myArgument has been cleared.
Type: Void
axiom
myhalf()==recip(2::EXPR INT)::EXPR INT
1 old definition(s) deleted for function or rule myhalf
Type: Void
axiom
pi1:= pi()$(EXPR INT)
Type: Expression(Integer)
axiom
pi2 := pi1 * myhalf()
axiom
Compiling function myhalf with type () -> Expression(Integer)
Type: Expression(Integer)
axiom
myatan2(x:EXPR INT, y: EXPR INT): EXPR INT ==
x = 0 => if y >= 0 then %pi else -%pi
-- Atan in (-pi/2,pi/2]
theta := atan(y * recip(x)::EXPR INT)
-- may create infinite loop if variables are used in input
-- in any case, why would atan give a result outside (-pi/2, pi/2]?
-- while theta <= -pi2 repeat theta := theta + pi1
-- while theta > pi2 repeat theta := theta - pi1
x >= 0 => theta -- I or IV
if y >= 0 then
theta + pi1 -- II
else
theta - pi1 -- III
Function declaration myatan2 : (Expression(Integer),Expression(
Integer)) -> Expression(Integer) has been added to workspace.
Type: Void
axiom
myatan2(1,-1)
There are 4 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Expression(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
axiom
Compiling function myatan2 with type (Expression(Integer),Expression
(Integer)) -> Expression(Integer)
Type: Expression(Integer)
axiom
myatan2(x,y)
There are 4 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Expression(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
myArgument: Complex EXPR INT -> EXPR INT
Type: Void
axiom
myArgument(x) ==
zero? real x =>
imag(x) > 0 => pi2
imag(x) < 0 => - pi2
error "myArgument not defined at (0,0)"
myatan2(real x, imag x)
1 old definition(s) deleted for function or rule myArgument
Type: Void
axiom
myArgument(-%i)
There are 4 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
NonNegativeInteger
Expression(Integer)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
axiom
Compiling function myArgument with type Complex(Expression(Integer))
-> Expression(Integer)Type: Expression(Integer)
axiom
myArgument(%i)
Type: Expression(Integer)
axiom
myArgument(3+5*%i)
There are 4 exposed and 1 unexposed library operations named <
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op <
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named <
with argument type(s)
Expression(Integer)
NonNegativeInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
axiom
Compiling function myatan2 with type (Expression(Integer),Expression
(Integer)) -> Expression(Integer)
Type: Expression(Integer)
axiom
myArgument(3-5*%i)
Type: Expression(Integer)
axiom
myArgument(-1+%i)
Type: Expression(Integer)
axiom
myArgument(2 - x*%i)
Type: Expression(Integer)
axiom
myArgument(0::Complex EXPR INT)
Error signalled from user code:
myArgument not defined at (0,0)
William
Dear William,
I think that the "usual sign convention" is a bad idea. myatan2(x,y) should return unevaluated, since there is no way of knowing in which quadrant x+%i*y is. That's why I proposed OrderedRing, in which case the answer is clear. We would have to think of the case of members of COMPLEX EXPR INT where we happen to know the quadrant.
Martin
Dear Martin:
Thanks, and yes, I was wrong again (shame on me): the range of the single argument atan does not cover 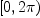 . But the only way to return results in case variables are involved in the arguments of
. But the only way to return results in case variables are involved in the arguments of atan(x,y) is to use provisos (I thought I was able to avoid this with the sign convention). Even if we were able to make EXPR INT into an OrderedRing, the tests such as if y > 0 then will have a different meaning than when y takes a value in INT whatever the ordering on EXPR INT may be. Such tests must be done using values of y, not the expression represented by y (thus, the code for myatan2 used these tests incorrectly for general expressions y). So it seems we need OrderedRing not on EXPR INT but on INT, which is okay, except that in COMPLEX R we have no way to know about what R is (see also last paragraph in this reply).
One possible way is to use a three argument atan : in addition to the x,y coordinates, also include the quadrant. This would allow a user to supply the crucial information and also make it automatic when the quadrant can be deduced. We can allow the quadrant information to be specified as unknown or failed and then return the expression unevaluated in that case.
The amount of simplification that should be carried out should also be part of the discussions. For example, in a two-argument version, atan(2*(x^2+1),(x^2+1)) should be evaluated to atan(1/2) but any such simplification either is difficult (not possible?) or may lose information on the quadrant if not carefully done. For example, atan(2*(x^2+1),-(x^2+1)) and atan(-2*(x^2+1), (x^2+1)) should give different answers. But how can we test signs on expressions? (Note that this is different from how to make EXPR INT into an OrderedRing because we are talking really on the level of the base domain: signs of expressions as values, not as expressions.) It would seem that we need to get into the full-blown cylindrical algebraic decomposition (CAD) stuff, even just for the polynomial expressions. And INT is not quite the base domain to perform these computations.
Stepping back a bit, let's see why EXPR INT is involved in the original post to evaluate argument(-%i). Functions (and especially, when implemented as operators) like argument and atan perhaps should be defined only under a domain which is closed with respect to them (so argument: Complex R -> R would be considered closed, but argument: Complex Integer -> Expression Integer would not.) In Complex Integer these functions are meaningful only because the set of Gaussian integers is mathematically a subset of the field of complex numbers. The Axiom construction is complicated by the fact that 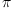 may be symbolic and hence lives in
may be symbolic and hence lives in Expression R. And once expanded to Expression R, the problem with what to do with variable inputs further complicates the implementation. Thus in evaluating argument((-1+%i)::Complex Integer), Axiom needs to invoke argument: Complex EXPR INT->EXPR INT. Would it be appropriate to invoke something like argument: Complex Float -> Float instead? (This would avoid the issue of variables in input arguments.)
This discussion naturally leads one to question why specific constants such as 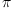 live in separate domains in Axiom (contrary to a purely mathematical model). Must these constants be numerically represented under
live in separate domains in Axiom (contrary to a purely mathematical model). Must these constants be numerically represented under Float? Can one create something called SymbolicFloat where roughly, SymbolicFloat is a mix of floating point numbers, symbolic algebraic numbers, and symbolic transcendental numbers, and yet retains the properties of RealNumberSystem and OrderedRing (so whenever an inequality in this domain is to be tested, all symbolic constants will be temporarily converted to floating point with an accuracy sufficient to resolve the decision, but the symbolic constants still remain symbolic in subsequent computations)?
William
see
#141 atan(tan(3)) => 3
Thanks for this pointer. I would prefer to classify
tan(3) as belonging to the hypothetical
SymbolicFloat rather than to
EXPR INT and the same for
atan(tan(3)). The definition of the single argument
atan chooses by convention a unique answer in
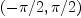
where
tan is monotone. Axiom is constrained by its type system to provide an answer within
EXPR INT and view
atan as a more generalized inverse (that is, no longer a
function) and multiple answers are possible. The (applied) scientific community probably prefers invoking the
Float or
DoubleFloat version of
atan and
tan, and they can, by simply changing
3 to
3.0.
see
RealNumbers and
#167 for more info and discussions on infinite precision floats and exact real number computations.
I think we could simply add a definition of a two argument version of
atan to
ElementaryFunction, where we can ask for
OrderedRing. I'll try to propose a definition tomorrow.
Martin
Status: fix proposed => open
Category: Axiom Mathematics => Axiom Library
Status: open => fix proposed
axiom
complexForm(%i*log(-%i) - %i*log(%i))
Type: Complex(Expression(Integer))
gives 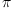 , as it should.
, as it should.
Status: fix proposed => fixed somewhere
No patch available.
http://fricas.svn.sourceforge.net/viewvc/fricas/trunk/src/algebra/gaussian.spad.pamphlet?r1=257&r2=358&view=patch
Status: fixed somewhere => fix proposed