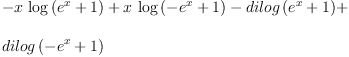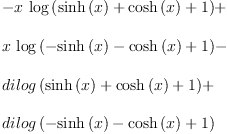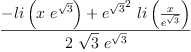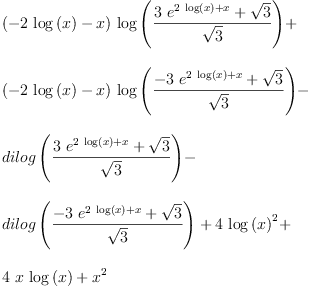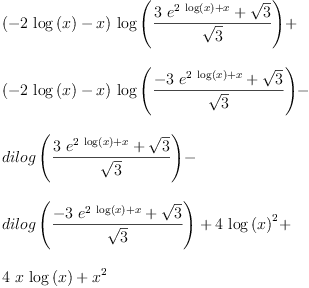FriCAS can now handle large class of integrals expressible in terms of exponential integral, error functions, incomplete Gamma function with constant first argument, logarithmic integral and polylogarithms. Like fricas (1) -> integrate(1/log(x),
Type: Union(Expression(Integer),
fricas integrate(1/(log(x) + 1),
Type: Union(Expression(Integer),
fricas integrate(1/(log(x)^2-1),
Type: Union(Expression(Integer),
fricas integrate(exp(x + a)/x,
Type: Union(Expression(Integer),
fricas integrate(exp(x + a)/x^2,
Type: Union(Expression(Integer),
fricas integrate(exp(x)/(x^2 - 1),
Type: Union(Expression(Integer),
fricas integrate(x/(exp(x) - 1),
Type: Union(Expression(Integer),
fricas integrate(x^3/(exp(x) - 1),
Type: Union(Expression(Integer),
fricas integrate(2*x*exp(x)/(exp(x)^2 - 1),
Type: Union(Expression(Integer),
fricas integrate(x/sinh(x),
Type: Union(Expression(Integer),
fricas )set output algebra on fricas )set output tex off Type: Union(Expression(Integer),
fricas )set output algebra off fricas )set output tex on fricas integrate(exp((-x^2-2*x-1)/x^2)/x^2,
Type: Union(Expression(Integer),
fricas integrate(x^3*exp(-x^3),
Type: Union(Expression(Integer),
fricas integrate(x^2*exp(-(x+1)^3),
Type: Union(Expression(Integer),
fricas integrate(x^n*exp(b*x^2),
Type: Union(Expression(Integer),
FriCAS can introduce new algebraic constants when needed: fricas integrate(1/(log(x)^2-3),
Type: Union(Expression(Integer),
fricas integrate(exp(x)/(x^2 - 5),
Type: Union(Expression(Integer),
The method is robust, FriCAS can handle both fricas integrate(((x+1)*exp(x))/log(x*exp(x)),
Type: Union(Expression(Integer),
fricas integrate(((x+1)*exp(x))/(x + log(x)),
Type: Union(Expression(Integer),
while Mathematca 12 can handle the first form, but not the second one (Maple 15 and Maxima 5.45.1 can not handle any). Similarly FriCAS has no troubles with fricas integrate(((-4*x-8)*log(x)+(-2*x^2-4*x))/(3*x*exp(2*log(x)+x)^2-x),
Type: Union(Expression(Integer),
fricas integrate(((-4*x-8)*log(x)+(-2*x^2-4*x))/(3*x^3*exp(log(x)+x)^2-x),
Type: Union(Expression(Integer),
fricas integrate(((2*x^4-x^3+3*x^2+2*x+2)*exp(x/(x^2+2)))/(x^3+2*x),
Type: Union(Expression(Integer),
None of Mathematca 12, Maple 15 and Maxima 5.45.1 can handle them. Since FriCAS uses algorithmic approach some integrals can be done easily without any extra special support. For example: fricas )set output tex off fricas )set output algebra on Type: Union(Expression(Integer),
fricas )set output tex on fricas )set output algebra off is done combining general support for Liouvillian integrands with procedure for handling erf. In Rubi this example required adding a new special rule. FriCAS can also handle some integrals involving special functions of algebraic arguments: fricas integrate(((26*x+23)*x^(1/2)+4*x^2+50*x-6)*exp(2*x^(1/2)+x)/((16*x^2+36*x)*x^(1/2)+(2*x^3+42*x^2)),
Type: Union(Expression(Integer),
There is also limited support to handle integrals where answer depends on elliptic functions: fricas integrate(1/sqrt((1 - x^2)*(1 + 2*x^2)),
Type: Union(Expression(Integer),
fricas integrate(1/sqrt(x^3 - 1),
Type: Union(Expression(Integer),
|
|
|
|
last edited 7 months ago by test1 |