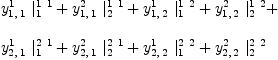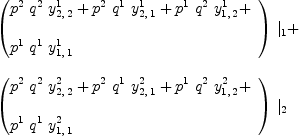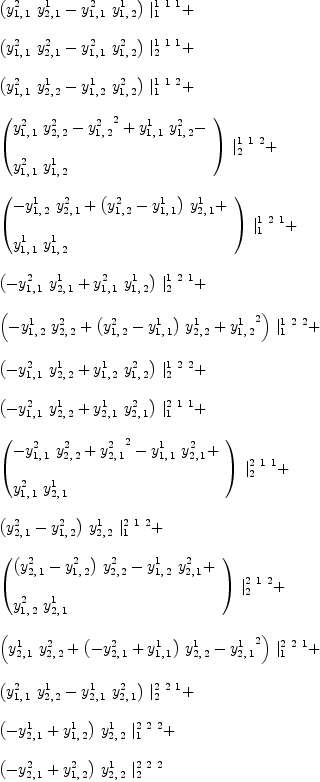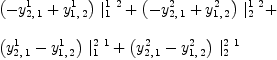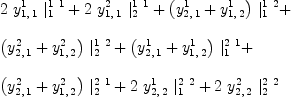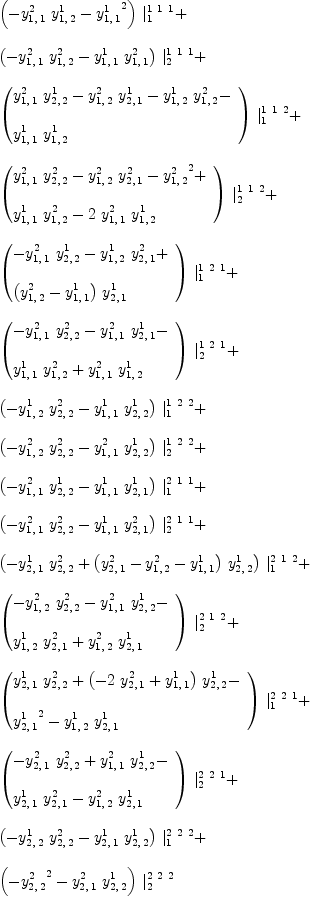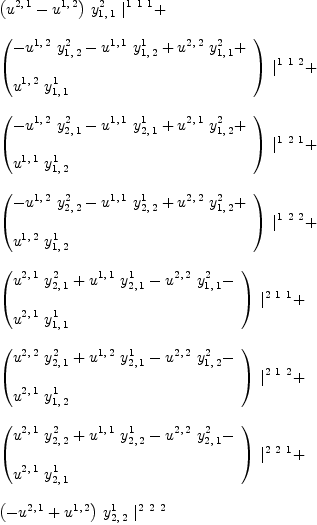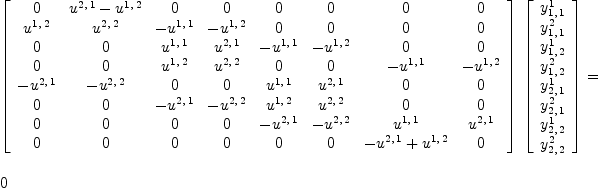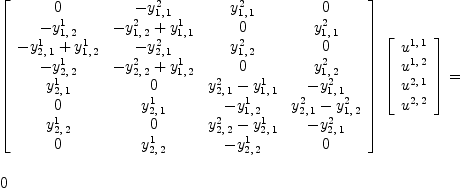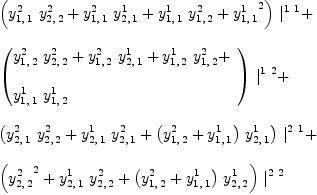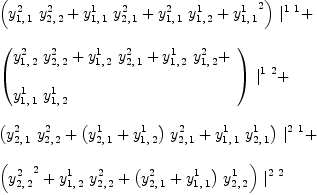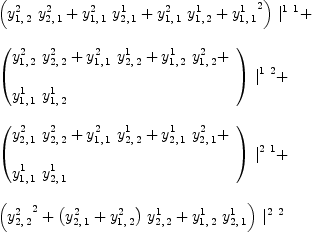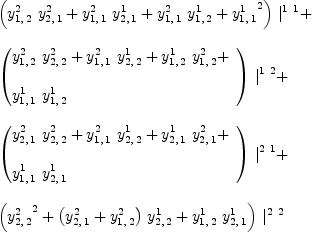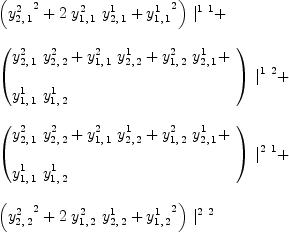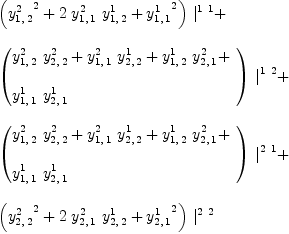References
See also:
2-d ExampleUse LinearOperator (LOP) fricas (1) -> )lib CARTEN MONAL PROP LOP
Type: Type
fricas -- basis dx:=basisIn()$L
fricas Dx:=basisOut()$L
fricas -- summation macro Σ(f, Type: Void
fricas -- identity I:L:=[1]
fricas -- twist X:L:=[2,
fricas -- co-evaluation Λ:L:=co(1)
fricas -- evaluation V:L:=ev(1)
Algebra An n-dimensional algebra is represented by a (2,1)-tensor
fricas Y:=Σ(Σ(Σ(script(y,
Multiplication Given two vectors fricas P:=Σ(script(p,
fricas Q:=Σ(script(q,
the tensor fricas R:=(P,
Pictorially:
P Q
Y
R
or more explicitly
Pi Qj
\/
\
Rk
AssociatorAn algebra is said to be associative if:
Y = Y
Y Y
i j k i j k i j k
\ | / \/ / \ \/
\ | / \ / \ /
\|/ = e k - i e
| \/ \/
| \ /
l l l
This requires that the following (3,1)-tensor
fricas YY := (Y,
Commutator The algebra
Y = Y
i j i j j i
\ / = \/ - \/
| \ /
k k k
This requires that the following (2,1)-tensor
fricas YC:=Y-(X/Y)
A basis for the ideal defined by the coefficients of the commutator is given by: fricas groebner(map(x+->x,
Type: List(Polynomial(Integer))
Anti-commutator The algebra
Y = -Y
i j i j j i
\ / = \/ = \/
| \ /
k k k
This requires that the following (2,1)-tensor
fricas YA:=Y+(X/Y)
A basis for the ideal defined by the coefficients of the commutator is given by: fricas groebner(map(x+->x,
Type: List(Polynomial(Integer))
JacobiThe Jacobi identity is:
X
Y = Y + Y
Y Y Y
i j k i j k i j k i j k
\ | / \ / / \ \ / \ \ /
\ | / \ / / \ \ / \ 0
\ | / \/ / \ \/ \/ \
\ | / \ / \ / \ \
\|/ = e k - i e - e j
| \/ \/ \/
| \ / /
l l l l
An algebra satisfies the Jacobi identity if and only if the following (3,1)-tensor
fricas YX := YY - (I,
Scalar Product A scalar product is denoted by the (2,0)-tensor
fricas U:=Σ(Σ(script(u,
Definition 1We say that the scalar product is associative if the tensor equation holds:
Y = Y
U U
In other words, if the (3,0)-tensor:
i j k i j k i j k
\ | / \/ / \ \/
\|/ = \ / - \ /
0 0 0
fricas YU := (Y,
Definition 2An algebra with a non-degenerate associative scalar product is called pre-Frobenius. We may consider the problem where multiplication Y is given,
and look for all associative scalar products This problem can be solved using linear algebra. fricas )expose MCALCFN Type: Matrix(Expression(Integer))
fricas yy := transpose matrix [concat(map(variables, Type: Matrix(Polynomial(Integer))
fricas K::OutputForm * yy::OutputForm = 0
Type: Equation(OutputForm?)
The matrix A necessary condition for the equation to have a non-trivial
solution is that the matrix Theorem 1All 2-dimensional pre-Frobenius algebras are symmetric. Proof: Consider the determinant of the matrix fricas Kd := factor(determinant(K)::DMP(concat map(variables,
Type: Factored(DistributedMultivariatePolynomial?([u[;1,
The scalar product must also be non-degenerate fricas Ud:DMP(concat map(variables,
therefore U must be symmetric. fricas nthFactor(Kd, Theorem 2All 2-dimensional algebras with associative scalar product are commutative. Proof: The basis of the null space of the symmetric
fricas YUS := (I, This defines a 4-parameter family of 2-d pre-Frobenius algebras fricas test(eval(YUS, Alternatively we may consider fricas J := jacobian(ravel(YU), Type: Matrix(Expression(Integer))
fricas uu := transpose matrix [concat(map(variables, Type: Matrix(Polynomial(Integer))
fricas J::OutputForm * uu::OutputForm = 0
Type: Equation(OutputForm?)
The matrix A necessary condition for the equation to have a non-trivial
solution is that all 70 of the 4x4 sub-matrices of fricas JP:=ideal concat concat concat
[[[[ determinant(
matrix([row(J,
Type: PolynomialIdeal?(Fraction(Integer),
fricas #generators(%)
Type: PositiveInteger?
Theorem 3If a 2-d algebra is associative, commutative, anti-commutative or if it satisfies the Jacobi identity then it is a pre-Frobenius algebra. Proof Consider the ideals of the associator, commutator, anti-commutator and Jacobi identity fricas YYI:=ideal(ravel(YY)::List FRAC POLY INT); Type: PolynomialIdeal?(Fraction(Integer),
fricas in?(JP,
Type: Boolean
fricas YCI:=ideal(ravel(YC)::List FRAC POLY INT); Type: PolynomialIdeal?(Fraction(Integer),
fricas in?(JP,
Type: Boolean
fricas YAI:=ideal(ravel(YA)::List FRAC POLY INT); Type: PolynomialIdeal?(Fraction(Integer),
fricas in?(JP,
Type: Boolean
fricas YXI:=ideal(ravel(YX)::List FRAC POLY INT); Type: PolynomialIdeal?(Fraction(Integer),
fricas in?(JP,
Type: Boolean
Y-formsThree traces of two graftings of an algebra gives six (2,0)-forms. Left snail and right snail:
LS RS
Y /\ /\ Y
Y ) ( Y
\/ \/
i j j i
\/ \/
\ /\ /\ /
e f \ / f e
\/ \ / \/
\ / \ /
f / \ f
\/ \/
fricas LS:=
( Y Λ )/ _
( Y I )/ _
V
fricas RS:=
( Λ Y )/ _
( I Y )/ _
V
fricas test(LS=RS)
Type: Boolean
Left and right deer:
RD LD
\ /\/ \/\ /
Y /\ /\ Y
Y ) ( Y
\/ \/
i j i j
\ /\ / \ /\ /
\ f \ / \ / f /
\/ \/ \/ \/
\ /\ /\ /
e / \ / \ e
\/ \ / \/
\ / \ /
f / \ f
\/ \/
fricas RD:=
( I Λ I ) / _
( Y X ) / _
( Y I ) / _
V
fricas LD:=
( I Λ I ) / _
( X Y ) / _
( I Y ) / _
V
fricas test(LD=RD)
Type: Boolean
fricas test(RD=RS)
Type: Boolean
fricas test(RD=LS)
Type: Boolean
Left and right turtles:
RT LT
/\ / / \ \ /\
( Y / \ Y )
\ Y Y /
\/ \/
i j i j
/\ / / \ \ /\
/ f / / \ \ f \
/ \/ / \ \/ \
\ \ / \ / /
\ e / \ e /
\ \/ \/ /
\ / \ /
\ f f /
\/ \/
fricas RT:=
( Λ I I ) / _
( I Y I ) / _
( I Y ) / _
V
fricas LT:=
( I I Λ ) / _
( I Y I ) / _
( Y I ) / _
V
fricas test(LT=RT)
Type: Boolean
The turles are symmetric fricas test(RT = X/RT)
Type: Boolean
fricas test(LT = X/LT)
Type: Boolean
Five of the six forms are independent. fricas test(RT=RS)
Type: Boolean
fricas test(RT=LS)
Type: Boolean
fricas test(RT=RD)
Type: Boolean
fricas test(LT=RS)
Type: Boolean
fricas test(LT=LS)
Type: Boolean
fricas test(LT=RD)
Type: Boolean
Associativity implies right turtle equals right snail and left turtle equals left snail. fricas in?(ideal(ravel(RT-RS)::List FRAC POLY INT),
Type: Boolean
fricas in?(ideal(ravel(LT-LS)::List FRAC POLY INT),
Type: Boolean
If the Jacobi identity holds then both snails are zero fricas in?(ideal(ravel(RS)::List FRAC POLY INT),
Type: Boolean
fricas in?(ideal(ravel(LS)::List FRAC POLY INT),
Type: Boolean
and right turtle and deer have opposite signs fricas in?(ideal(ravel(RT+RD)::List FRAC POLY INT),
Type: Boolean
|
|
|
|
last edited 1 year ago by Bill Page |