Author: Martin Rubey A more thorough discussion of this package can be found at http://arxiv.org/abs/math.CO/0702086 fricas (1) -> )set output tex off fricas )set output algebra on If you find a bug please report in FriCAS BugTracker. Finally, please feel free to try this package in the SandBox! If you would like to use this program at your own computer, you need to install FriCAS. If you find the package useful, please let me know! Abstract
We present a software package that guesses formulas for sequences of, for
example, rational numbers or rational functions, given the first few terms.
Thereby we extend and complement Christian Krattenthaler's program This research was partially supported by the Austrian Science Foundation FWF, grant S8302-MAT. IntroductionFor some a brain-teaser, for others one step in proving their next theorem: given the first few terms of a sequence of, say, integers, what is the next term, what is the general formula? Of course, no unique solution exists, however, by Occam's razor, we will prefer a "simple" formula over a more "complicated" one. Some sequences are very easy to "guess", like
Others are a little harder, for example
Of course, at times we might want to guess a formula for a sequence of polynomials, too:
Fortunately, with the right tool, it is a matter of a moment to figure out
formulas for all of these sequences. In this article we describe a computer
program that encompasses well known techniques and adds new ideas that we hope
to be very effective. In particular, we generalize both Christian
Krattenthaler's program We would also like to mention The online encyclopedia of integer
sequences of Neil Sloane. There, you can enter a sequence of
integers and chances are good that the website will respond with one or more
likely matches. However, the approach taken is quite different from ours: the
encyclopedia keeps a list of currently Thus, the two approaches complement each other: For example, there are sequences where no simple formula is likely to exist, and which can thus be found only in the encyclopedia. On the other hand, there are many sequences that have not yet found their way into the encyclopedia, but can be guessed in a few minutes by your computer. On the historical side, we remark that already in 1966 Paul W. Abrahams implemented a program to identify sequences given their first few terms... Safety and Speed A formula for Sequence (1) is almost trivial to guess: it
seems obvious that it is Apart from safety, the main problem we have to solve is about efficiency. For
example, maybe we would like to test whether the
Thus, we need to find efficient algorithms that test for large classes of formulas. Obviously, such algorithms exist for interpolation and Pade approximation. For the present package, we implemented an efficient algorithm for a far reaching generalization of interpolation, proposed by Bernhard Beckermann and George Labahn, see FractionFreeFastGaussianElimination. Furthermore, we show that there is also a way to guess sequences generated by Formula (6). Using these algorithms our package clearly outperforms both In the following section we outline the capabilities of our package. In the Section therafter we describe the most important options that modify the behaviour of the functions. Function Classes Suitable for Guessing In this section we briefly present the function classes which are covered by
our package. Throughout this section, Guessing
|
| (7) |
guessRec([1,1, 0, 1, - 1, 2, - 1, 5, - 4, 29, - 13, 854, - 685])
2 (1) [[f(n): f(n + 2) + f(n + 1) - f(n) = 0,f(0) = 1, f(1) = 1]]
Note that, at least in the current implementation, we do not exclude
solutions that do not determine the function ![]() completely. For example,
given a list containing only zeros and ones, one result will be
completely. For example,
given a list containing only zeros and ones, one result will be
guessPRec only looks for recurrences with linear guessPRec([0,1, 0, -1/6, 0, 1/120, 0, -1/5040, 0, 1/362880, 0, -1/39916800])
(2) []
Concerning ![]() -analogues,
-analogues, guessRec(q) finds recurrences of the
form (7), where ![]() is a polynomial with coefficients in
is a polynomial with coefficients in ![]() .
Similarly, we provide
.
Similarly, we provide ![]() -analogues for
-analogues for guessPRec and
guessRat. Finally, guessExpRat(q) recognizes functions of the form
For Sequence (5), we enter
guessExpRat(q)([(1-2*q)/(1-q),1-2*q, (1-q)*(1-2*q)^3, (1-q)^2*(1-2*q)*(1-2*q-2*q^2)^3], [])
n n (2 q - 1)(2 q - 3 q + 1) (4) [--------------------------] q - 1
Guessing 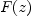
guessADEfinds an algebraic differential equation for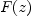 ,
i.e., an equation of the form
,
i.e., an equation of the form
where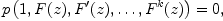
(8) 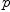 is a polynomial with coefficients in
is a polynomial with coefficients in ![\mathbb K[z] \mathbb K[z]](images/4426617896344486831-16.0px.png) . A typical
example is
. A typical
example is 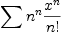 :
fricas
:
fricasguessADE([1,
1, 2, 9/2, 32/3, 625/24, 324/5, 117649/720, 131072/315])
(5) []Type: List(Expression(Integer))guessHoloonly looks for equations of the form (11) with linear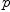 , that is, it recognizes holonomic or differentially-finite
functions. It is well known that the class of holonomic functions coincides
with the class of functions having P-recursive Taylor coefficients. However,
the number of terms necessary to find the differential equation often differs
greatly from the number of terms necessary to find the recurrence. Returning
to the example given for
, that is, it recognizes holonomic or differentially-finite
functions. It is well known that the class of holonomic functions coincides
with the class of functions having P-recursive Taylor coefficients. However,
the number of terms necessary to find the differential equation often differs
greatly from the number of terms necessary to find the recurrence. Returning
to the example given for guessPRec, we find that already the first 6 terms are sufficient to guess a generating function:fricasguessHolo([0,
1, 0, -1/6, 0, 1/120])
3 n ,, x 4 (6) [[[x ]f(x): f (x) + f(x) = 0, f(x) = x - -- + O(x )]] 6 Type: List(Expression(Integer))Moreover, now we immediately recognise the coefficients as being those of the sine function.
guessHolois also the function provided byGFUN. Here is a comparison of average running times in seconds over several runs on the same machine for a list of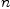 elements
elements

guessAlglooks for an algebraic equation satisfied by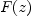 ,
i.e., an equation of the form
,
i.e., an equation of the form
the prime example being given by the Catalan numbers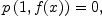 fricas
fricasfirst guessAlg [1,
1, 2, 5, 14, 42]
n 2 2 3 4 (7) [[x ]f(x): x f(x) - f(x) + 1 = 0,f(x) = 1 + x + 2 x + 5 x + O(x )] Type: Expression(Integer)guessPaderecognises rational generating functions. For the Fibonacci sequence given in Equation (2), we find as likely solution![[[x^n ]f(x): (x^2 + x - 1)f(x) + 1= 0].
[[x^n ]f(x): (x^2 + x - 1)f(x) + 1= 0].](images/7995021689917122275-16.0px.png)
We provide ![]() -analogues, replacing differentiation with
-analogues, replacing differentiation with ![]() -dilation:
-dilation:
guessADE(q) finds differential equations of the form
| (9) |
guessHolo, guessAlg, and guessPade.
To guess a formula for Sequence (4), we enter
guessRat(q)([1,1+q+q^2, (1+q+q^2)*(1+q^2), (1+q^2)*(1+q+q^2+q^3+q^4)], [])
3 2 n 2 n q q + (- q - q)q + 1 (8) [-------------------------] 3 2 q - q - q + 1
Operators
The main observation made by Christian Krattenthaler in designing his program
Rate is the following: it occurs frequently that although a sequence of numbers
is not generated by a rational function, the sequence of successive quotients is.
We slightly extend upon this idea, and apply recursively one or both of the two following operators:
guessSum-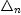 the differencing operator, transforming
the differencing operator, transforming
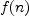 into
into 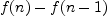 .
.guessProduct-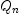 the operator that transforms
the operator that transforms 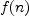 into
into
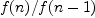 .
.
For example, to guess a formula for Sequence (3), we enter
guess([0,1, 3, 9, 33], [guessRat], [guessSum, guessProduct])
s - 1 n - 1 5 --+ ++-++ (9) [ > | | p + 2] --+ | | 4 s = 0 p = 0 5 4
The second argument to guess indicates which of the functions of the
previous section to apply to each of the generated sequence, while the third
argument indicates which operators to use to generate new sequences.
In the case where only the operator ![]() is applied, our package is directly
comparable to
is applied, our package is directly
comparable to Rate. In this case the standard example is the number of
alternating sign matrices
guess([1,1, 2, 7, 42, 429, 7436, 218348], [guessRat], [guessProduct])
p - 1 2 n - 1 8 27 p + 54 p + 24 ++-++ ++-++ 7 7 (10) [ | | | | -------------------] | | | | 2 p = 0 p = 0 16 p + 32 p + 12 8 7 7 7
Here are the average running times in seconds for our package and Rate over
several runs on the same machine for a list of ![]() elements:
elements:
Options
To give you the maximum flexibility in guessing a formula for your favourite sequence, we provide options that modify the behaviour of the functions as described in Section~\ref{sec:function-classes}. The options are appended, separated by commas, to the guessing function in the form \spad{option==value}. See below for some examples.
debugspecifies whether informations about progress should be reported.safetyspecifies, as explained at the beginning of Section 2, the number of values reserved for testing any solutions found. The default setting is 1.Experiments seem to indicate that for
guessADEhigher settings are appropriate than forguessRat. I.e., if a rational function interpolates the given list of terms, where the final term is used for testing, we can be pretty sure that the formula found is correct. By contrast, we recommend settingsafetyto 3 or 4 when usingguessADE. For all algorithms exceptguessExpRatwe recommend to omit trailing zeros.onespecifies whether the guessing function should return as soon as at least one solution is found. By default, this option is set totrue.maxDegreespecifies the maximum degree of the coefficient polynomials in an algebraic differential equation or a recursion with polynomial coefficients. For rational functions with an exponential term,maxDegreebounds the degree of the denominator polynomial. This option is especially interesting if trying rather long sequences where it is unclear whether a solution will be found or not. SettingmaxDegreeto -1, which is the default, specifies that the maximum degree can be arbitrary.allDegreesspecifies whether all possibilities of the degree vector - taking into accountmaxDegree- should be tried. The default istrueforguessPadeandguessRatandfalsefor all other functions.homogeneousspecifies whether the search space should be restricted to homogeneous algebraic differential equations or homogeneous recurrences. By default, it is set tofalse.maxDerivative-maxShiftspecify the maximum derivative in an algebraic differential equation, or, in a recurrence relation, the maximum shift. Setting the option to -1 specifies that the maximum derivative - the maximum shift - may be arbitrary.maxPowerspecifies the maximum total degree in an algebraic differential equation or recurrence: for example, the degree of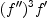 is 4. Setting the option to -1 specifies that the maximum total degree
may be arbitrary. For example,
fricas
is 4. Setting the option to -1 specifies that the maximum total degree
may be arbitrary. For example,
fricasl := [1,
1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, 126742987, 1687054711, 47301104551, 1123424582771, 32606721084786, 1662315215971057]; Type: List(PositiveInteger?)fricasguessRec(l,
maxPower==2)
(12) [ 2 [f(n): - f(n)f(n + 4) + f(n + 1)f(n + 3) + f(n + 2) = 0,f(0) = 1, f(1) = 1, f(2) = 1, f(3) = 1] ] Type: List(Expression(Integer))returns the Somos-4 recurrence, whereas without limiting the power to 2, we need the first 33 values, and instead of roughly one second half a minute of computing time.
maxLevelspecifies how many levels of recursion are tried when applying operators. Note that, applying either of the two operators results in a sequence which is by one shorter than the original sequence. Therefore, in case bothguessSumandguessProductare specified, the number of times a guessing algorithm from the given list of functions is applied is roughly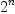 , where
$n$ is the number of terms in the given sequence. Thus, especially when the
list of terms is long, it is important to set
, where
$n$ is the number of terms in the given sequence. Thus, especially when the
list of terms is long, it is important to set maxLevelto a low value.Still, the default value is -1, which means that the number of levels is only restricted by the number of terms given in the sequence.
indexName,variableName,functionNamespecify symbols to be used for the output. The defaults aren,xandfrespectively.
A note on the output
The output of any function described in Section 3 is a list of formulae which seem to fit, along with an integer that states from which term on the formula is correct. The latter is necessary, because rational interpolation features sometimes unattainable points, as the following example shows:
guessRat([3,4, 7/2, 18/5, 11/3, 26/7])
2 2 (13) [[f(n): (- n - n + 2)f(n) + 4 n + 2 n - 6 = 0]]
![]() indicates that the first two terms of the sequence might not
coincide with the value predicted by the returned function. A similar situation
occurs, if the function generating the sequence has a singular point at
indicates that the first two terms of the sequence might not
coincide with the value predicted by the returned function. A similar situation
occurs, if the function generating the sequence has a singular point at
![]() , where
, where ![]() and
and ![]() is the number of given
values. We would like to stress that this is rather a feature than a
bug: most terms will be correct, just as in the example above, where the
value at
is the number of given
values. We would like to stress that this is rather a feature than a
bug: most terms will be correct, just as in the example above, where the
value at ![]() is indeed 3.
is indeed 3.
)version
"FriCAS 1.3.10 compiled at Wed 10 Jan 02:19:45 CET 2024"