|
|
|
last edited 9 years ago by test1 |
Edit detail for Guessing formulas for sequences revision 1 of 15
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | ||
|
Editor: 127.0.0.1
Time: 2007/11/06 20:57:52 GMT-8 |
||
| Note: copied from axiom-developer | ||
changed: - Author: "Martin Rubey":http://www.mat.univie.ac.at/~rubey/martin.html Important Note There is a bug (#8) in the version of Axiom currently running on this server that messes up the output by missing some parenthesis. A preliminary - though a little unsatisfactory - patch is available. We hope that a proper fix will soon be applied. Please add other bugs you find to IssueTracker by clicking on "Bug reports":http://wiki.axiom-developer.org/IssueTracker on the top left of any page and filling out the appropriate forms. Finally, please feel free to try this package in the "SandBox":SandBoxGuessingSequence! If you would like to use this program at your own computer, you need the files - [ssolve.spad.pamphlet] from SeriesSolve - [rec.spad.pamphlet] from RecurrenceRelationOperator - [fffg.spad.pamphlet] from FractionFreeFastGaussianElimination and - [mantepse.spad.pamphlet] If you find the package useful, please let me know! Abstract We present a software package that guesses formulas for sequences of, for example, rational numbers or rational functions, given the first few terms. Thereby we extend and complement Christian Krattenthaler's program 'Rate' and the relevant parts of Bruno Salvy and Paul Zimmermann's 'GFUN'. This research was partially supported by the Austrian Science Foundation FWF, grant S8302-MAT. Introduction For some a brain-teaser, for others one step in proving their next theorem: given the first few terms of a sequence of, say, integers, what is the next term, what is the general formula? Of course, no unique solution exists, however, by Occam's razor, we will prefer a "simple" formula over a more "complicated" one. Some sequences are very easy to "guess", like \begin{equation} 1,4,9,16,\dots, \end{equation} or \begin{equation} 1,1,2,3,5,\dots. \end{equation} Others are a little harder, for example \begin{equation} 0,1,3,9,33,\dots. \end{equation} Of course, at times we might want to guess a formula for a sequence of polynomials, too: \begin{equation} 1,1+q+q^2,(1+q+q^2)(1+q^2),(1+q^2)(1+q+q^2+q^3+q^4)\dots, \end{equation} or \begin{equation} \frac{1-2q}{1-q}, 1-2q,(1-q)(1-2q)^3,(1-q)^2(1-2q)(1-2q-2q^2)^3,\dots \end{equation} Fortunately, with the right tool, it is a matter of a moment to figure out formulas for all of these sequences. In this article we describe a computer program that encompasses well known techniques and adds new ideas that we hope to be very effective. Fortunately, with the right tool, it is a matter of a moment to figure out formulas for all of these sequences. In this article we describe a computer program that encompasses well known techniques and adds new ideas that we hope to be very effective. In particular, we generalize both Christian Krattenthaler's program 'Rate', and the guessing functions present in 'GFUN' written by Bruno Salvy and Paul Zimmermann. With a little manual aid, we can guess multivariate formulas as well, along the lines of Doron Zeilberger's programs 'GuessRat' and 'GuessHolo'. We would also like to mention The online encyclopedia of integer sequences of Neil Sloane. There, you can enter a sequence of integers and chances are good that the website will respond with one or more likely matches. However, the approach taken is quite different from ours: the encyclopedia keeps a list of currently $117,520$ sequences, entered more or less manually, and it compares the given sequence with each one of those. Besides that, it tries some simple transformations on the given sequence to find a match. Furthermore it tries some simple programs we will describe below to find a formula, although with a time limit, i.e., it gives up when too much time has elapsed. Thus, the two approaches complement each other: For example, there are sequences where no simple formula is likely to exist, and which can thus be found only in the encyclopedia. On the other hand, there are many sequences that have not yet found their way into the encyclopedia, but can be guessed in a few minutes by your computer. On the historical side, we remark that already in 1966 Paul W. Abrahams implemented a program to identify sequences given their first few terms... Safety and Speed A formula for Sequence (1) is almost trivial to guess: it seems obvious that it is $n^2$. More generally, if we believe that the sequence in question is generated by a polynomial, we can simply apply interpolation. However, how can we know that a polynomial formula is appropriate? The answer is quite simple: we use all but the last few terms of the sequence to derive the formula. After this, the last terms are compared with the values predicted by the polynomial. If they coincide, we can be confident that the guessed formula is correct. We call the number of terms used for checking the formula the safety of the result. Apart from safety, the main problem we have to solve is about efficiency. For example, maybe we would like to test whether the $n^{th}$ term of the sequence is given by a formula of the form \begin{equation} n\mapsto (a+bn)^n \frac{r(n)}{s(n)} \end{equation} for some $a$ and $b$ and polynomials $r$ and $s$. Of course, we could set up an appropriate system of polynomial equations. However, it would usually take a very long time to solve this system. Thus, we need to find efficient algorithms that test for large classes of formulas. Obviously, such algorithms exist for interpolation and Pade approximation. For the present package, we implemented an efficient algorithm for a far reaching generalization of interpolation, proposed by Bernhard Beckermann and George Labahn, see FractionFreeFastGaussianElimination. Furthermore, we show that there is also a way to guess sequences generated by Formula (6). Using these algorithms our package clearly outperforms both 'Rate' and 'GFUN', in terms of speed as well as in the range of formulas that can be guessed. In the following section we outline the capabilities of our package. In the Section therafter we describe the most important options that modify the behaviour of the functions. Function Classes Suitable for Guessing In this section we briefly present the function classes which are covered by our package. Throughout this section, $n\mapsto f(n)$ is the function we would like to guess, and $F(z)=\sum_{n\ge0} f(n)z^n$ is its generating function. The values $f(n)$ are supposed to be elements of some field $\mathbb K$, usually the field of rationals or rational functions. We alert the reader that the first value in the given sequence always corresponds to the value $f(0)$. To load the package we type \begin{axiom} )lib RECOP FAMR2 FFFG FFFGF NEWTON UFPS UFPS1 GOPT GOPT0 GUESS GUESSINT GUESSP GUESSF1 GUESSF \end{axiom} Guessing $f(n)$ - 'guessRec' finds recurrences of the form \begin{equation} p\left(1, f(n), f(n+1),\dots,f(n+k)\right)=0, \end{equation} where $p$ is a polynomial with coefficients in $\mathbb K[n]$. For example, \begin{axiom} guessRec([1,1,0,1,- 1,2,- 1,5,- 4,29,- 13,854,- 685]).1.function \end{axiom} Note that, at least in the current implementation, we do not exclude solutions that do not determine the function $f$ completely. For example, given a list containing only zeros and ones, one result will be \begin{equation*} [f(n): f(n)^2-f(n)=0,f(0)=\dots]. \end{equation*} - 'guessPRec' only looks for recurrences with linear $p$, i.e., it recognizes P-recursive sequences. As an example, \begin{axiom} guessPRec([0, 1, 0, -1/6, 0, 1/120, 0, -1/5040, 0, 1/362880, 0, -1/39916800]).1.function \end{axiom} - 'guessRat' finds rational functions. For the sequence given in Equation (1), we find $n^2$ as likely solution. - 'guessExpRat' finds rational functions with an Abelian term, i.e., \begin{equation*} f(n)=(a+bn)^n\frac{r(n)}{s(n)} \end{equation*} where $r$ and $s$ are polynomials. \begin{axiom} guessExpRat([0,3,32,375,5184,84035]).1.function \end{axiom} Concerning $q$-analogues, 'guessRec(q)' finds recurrences of the form (7), where $p$ is a polynomial with coefficients in $\mathbb K[q, q^n]$. Similarly, we provide $q$-analogues for 'guessPRec' and 'guessRat'. Finally, 'guessExpRat(q)' recognizes functions of the form \begin{equation*} f(n)=(a+bq^n)^n\frac{r(q^n)}{s(q^n)}, \end{equation*} $a$ and $b$ being in $\mathbb K[q]$ and $r$ and $s$ polynomials with coefficients in $\mathbb K[q]$. This includes, for example, Nicholas Loehr's $q$-analogue $[n+1]_q^{n-1}$ of Cayley's formula, where $[n]_q=1+q+\dots+q^{n-1}$. For Sequence (5), we enter \begin{axiom} guessExpRat(q)([(1-2*q)/(1-q),1-2*q,(1-q)*(1-2*q)^3,(1-q)^2*(1-2*q)*(1-2*q-2*q^2)^3], []).1.function \end{axiom} Guessing $F(z)$ - 'guessADE' finds an algebraic differential equation for $F(z)$, i.e., an equation of the form \begin{equation} p\left(1, F(z), F^\prime(z),\dots,F^{k}(z)\right)=0, \end{equation} where $p$ is a polynomial with coefficients in $\mathbb K[z]$. A typical example is $\sum n^n\frac{x^n}{n!}$: \begin{axiom} guessADE([1,1,2,9/2,32/3,625/24,324/5,117649/720,131072/315]).1.function \end{axiom} - 'guessHolo' only looks for equations of the form (11) with linear $p$, that is, it recognizes holonomic or differentially-finite functions. It is well known that the class of holonomic functions coincides with the class of functions having P-recursive Taylor coefficients. However, the number of terms necessary to find the differential equation often differs greatly from the number of terms necessary to find the recurrence. Returning to the example given for 'guessPRec', we find that already the first 6 terms are sufficient to guess a generating function: \begin{axiom} guessHolo([0,1,0,-1/6,0,1/120]).1.function \end{axiom} Moreover, now we immediately recognise the coefficients as being those of the sine function. 'guessHolo' is also the function provided by 'GFUN'. Here is a comparison of average running times in seconds over several runs on the same machine for a list of $n$ elements \begin{tabular}{lrrrrrrrrrr} $n$: & 50 & 75 & 100 & 125 \\ GFUN: & 1.9 & 5.2 & 22.1 & 63.0 \\ Guess: & 0.1 & 0.3 & 0.6 & 1.2 \end{tabular} - 'guessAlg' looks for an algebraic equation satisfied by $F(z)$, i.e., an equation of the form \begin{equation*} p\left(1, f(x)\right)=0, \end{equation*} the prime example being given by the Catalan numbers \begin{axiom} guessAlg([1,1,2,5]).1.function \end{axiom} - 'guessPade' recognises rational generating functions. For the Fibonacci sequence given in Equation (2), we find as likely solution \begin{equation*} [[x^n ]f(x): (x^2 + x - 1)f(x) + 1= 0]. \end{equation*} We provide $q$-analogues, replacing differentiation with $q$-dilation: 'guessADE(q)' finds differential equations of the form \begin{equation} p\left(1, F(z), F(qz),\dots,F(q^kz)\right)=0, \end{equation} where $p$ is a polynomial with coefficients in $\mathbb K[q, z]$. Similarly, there are $q$-analogues for 'guessHolo', 'guessAlg', and 'guessPade'. To guess a formula for Sequence (4), we enter \begin{axiom} guessRat(q)([1,1+q+q^2,(1+q+q^2)*(1+q^2),(1+q^2)*(1+q+q^2+q^3+q^4)], []).1.function \end{axiom} Operators The main observation made by Christian Krattenthaler in designing his program 'Rate' is the following: it occurs frequently that although a sequence of numbers is not generated by a rational function, the sequence of successive quotients is. We slightly extend upon this idea, and apply recursively one or both of the two following operators: - 'guessSum' - $\Delta_n$ the differencing operator, transforming $f(n)$ into $f(n)-f(n-1)$. - 'guessProduct' - $Q_n$ the operator that transforms $f(n)$ into $f(n)/f(n-1)$. For example, to guess a formula for Sequence (3), we enter \begin{axiom} guess([0, 1, 3, 9, 33], [guessRat], [guessSum, guessProduct]).1.function \end{axiom} The second argument to 'guess' indicates which of the functions of the previous section to apply to each of the generated sequence, while the third argument indicates which operators to use to generate new sequences. In the case where only the operator $Q_n$ is applied, our package is directly comparable to 'Rate'. In this case the standard example is the number of alternating sign matrices \begin{axiom} guess([1, 1, 2, 7, 42, 429, 7436, 218348], [guessRat], [guessProduct]).1.function \end{axiom} Here are the average running times in seconds for our package and 'Rate' over several runs on the same machine for a list of $n$ elements: \begin{tabular}{lrrrrrrrrrr} $n$: & 14 & 15 & 16 & 17 & 18\\ Rate: & 1.0 & 3.3 & 29.7 & 44.9 & 398\\ Guess: & 0.9 & 2.3 & 6.6 & 22.4 & 74 \end{tabular} Options To give you the maximum flexibility in guessing a formula for your favourite sequence, we provide options that modify the behaviour of the functions as described in Section~\ref{sec:function-classes}. The options are appended, separated by commas, to the guessing function in the form \spad{option==value}. See below for some examples. - 'debug' specifies whether informations about progress should be reported. - 'safety' specifies, as explained at the beginning of Section 2, the number of values reserved for testing any solutions found. The default setting is 1. Experiments seem to indicate that for 'guessADE' higher settings are appropriate than for 'guessRat'. I.e., if a rational function interpolates the given list of terms, where the final term is used for testing, we can be pretty sure that the formula found is correct. By contrast, we recommend setting 'safety' to 3 or 4 when using 'guessADE'. For all algorithms except 'guessExpRat' we recommend to omit trailing zeros. - 'one' specifies whether the guessing function should return as soon as at least one solution is found. By default, this option is set to 'true'. - 'maxDegree' specifies the maximum degree of the coefficient polynomials in an algebraic differential equation or a recursion with polynomial coefficients. For rational functions with an exponential term, 'maxDegree' bounds the degree of the denominator polynomial. This option is especially interesting if trying rather long sequences where it is unclear whether a solution will be found or not. Setting 'maxDegree' to -1, which is the default, specifies that the maximum degree can be arbitrary. - 'allDegrees' specifies whether all possibilities of the degree vector - taking into account 'maxDegree' - should be tried. The default is 'true' for 'guessPade' and 'guessRat' and 'false' for all other functions. - 'homogeneous' specifies whether the search space should be restricted to homogeneous algebraic differential equations or homogeneous recurrences. By default, it is set to 'false'. - 'maxDerivative' - 'maxShift' specify the maximum derivative in an algebraic differential equation, or, in a recurrence relation, the maximum shift. Setting the option to -1 specifies that the maximum derivative - the maximum shift - may be arbitrary. - 'maxPower' specifies the maximum total degree in an algebraic differential equation or recurrence: for example, the degree of $(f'')^3 f'$ is 4. Setting the option to -1 specifies that the maximum total degree may be arbitrary. For example, \begin{axiom} l := [1, 1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, 126742987, 1687054711, 47301104551, 1123424582771, 32606721084786, 1662315215971057]; guessRec(l, maxPower==2).1.function \end{axiom} returns the Somos-4 recurrence, whereas without limiting the power to 2, we need the first 33 values, and instead of roughly one second half a minute of computing time. - 'maxLevel' specifies how many levels of recursion are tried when applying operators. Note that, applying either of the two operators results in a sequence which is by one shorter than the original sequence. Therefore, in case both 'guessSum' and 'guessProduct' are specified, the number of times a guessing algorithm from the given list of functions is applied is roughly $2^n$, where $n$ is the number of terms in the given sequence. Thus, especially when the list of terms is long, it is important to set 'maxLevel' to a low value. Still, the default value is -1, which means that the number of levels is only restricted by the number of terms given in the sequence. - 'indexName', 'variableName', 'functionName' specify symbols to be used for the output. The defaults are 'n', 'x' and 'f' respectively. A note on the output The output of any function described in Section 3 is a list of formulae which seem to fit, along with an integer that states from which term on the formula is correct. The latter is necessary, because rational interpolation features sometimes unattainable points, as the following example shows: \begin{axiom} guessRat([3, 4, 7/2, 18/5, 11/3, 26/7]) \end{axiom} $order=2$ indicates that the first two terms of the sequence might not coincide with the value predicted by the returned function. A similar situation occurs, if the function generating the sequence has a singular point at $n_0\in\mathbb N$, where $0 \leq n_0 < m$ and $m$ is the number of given values. We would like to stress that this is rather a feature than a bug: most terms will be correct, just as in the example above, where the value at $n=0$ is indeed 3.
Author: Martin Rubey
Important Note
There is a bug (#8) in the version of Axiom currently running on this server that messes up the output by missing some parenthesis. A preliminary - though a little unsatisfactory - patch is available. We hope that a proper fix will soon be applied.
Please add other bugs you find to IssueTracker? by clicking on Bug reports on the top left of any page and filling out the appropriate forms.
Finally, please feel free to try this package in the SandBox?! If you would like to use this program at your own computer, you need the files
- [ssolve.spad.pamphlet]? from SeriesSolve?
- [rec.spad.pamphlet]? from RecurrenceRelationOperator?
- [fffg.spad.pamphlet]? from FractionFreeFastGaussianElimination? and
- [mantepse.spad.pamphlet]?
If you find the package useful, please let me know!
Abstract
We present a software package that guesses formulas for sequences of, for
example, rational numbers or rational functions, given the first few terms.
Thereby we extend and complement Christian Krattenthaler's program Rate and
the relevant parts of Bruno Salvy and Paul Zimmermann's GFUN.
This research was partially supported by the Austrian Science Foundation FWF, grant S8302-MAT.
Introduction
For some a brain-teaser, for others one step in proving their next theorem: given the first few terms of a sequence of, say, integers, what is the next term, what is the general formula? Of course, no unique solution exists, however, by Occam's razor, we will prefer a "simple" formula over a more "complicated" one.
Some sequences are very easy to "guess", like
| (1) |
| (2) |
Others are a little harder, for example
| (3) |
Of course, at times we might want to guess a formula for a sequence of polynomials, too:
| (4) |
| (5) |
Fortunately, with the right tool, it is a matter of a moment to figure out formulas for all of these sequences. In this article we describe a computer program that encompasses well known techniques and adds new ideas that we hope to be very effective.
Fortunately, with the right tool, it is a matter of a moment to figure out
formulas for all of these sequences. In this article we describe a computer
program that encompasses well known techniques and adds new ideas that we hope
to be very effective. In particular, we generalize both Christian
Krattenthaler's program Rate, and the guessing functions present
in GFUN written by Bruno Salvy and Paul Zimmermann. With a little
manual aid, we can guess multivariate formulas as well, along the lines of
Doron Zeilberger's programs GuessRat and GuessHolo.
We would also like to mention The online encyclopedia of integer
sequences of Neil Sloane. There, you can enter a sequence of
integers and chances are good that the website will respond with one or more
likely matches. However, the approach taken is quite different from ours: the
encyclopedia keeps a list of currently ![]() sequences, entered more or
less manually, and it compares the given sequence with each one of those.
Besides that, it tries some simple transformations on the given sequence to
find a match. Furthermore it tries some simple programs we will describe below
to find a formula, although with a time limit, i.e., it gives up when too much
time has elapsed.
sequences, entered more or
less manually, and it compares the given sequence with each one of those.
Besides that, it tries some simple transformations on the given sequence to
find a match. Furthermore it tries some simple programs we will describe below
to find a formula, although with a time limit, i.e., it gives up when too much
time has elapsed.
Thus, the two approaches complement each other: For example, there are sequences where no simple formula is likely to exist, and which can thus be found only in the encyclopedia. On the other hand, there are many sequences that have not yet found their way into the encyclopedia, but can be guessed in a few minutes by your computer.
On the historical side, we remark that already in 1966 Paul W. Abrahams implemented a program to identify sequences given their first few terms...
Safety and Speed
A formula for Sequence (1) is almost trivial to guess: it
seems obvious that it is ![]() . More generally, if we believe that the sequence
in question is generated by a polynomial, we can simply apply interpolation.
However, how can we know that a polynomial formula is appropriate? The
answer is quite simple: we use all but the last few terms of the sequence to
derive the formula. After this, the last terms are compared with the values
predicted by the polynomial. If they coincide, we can be confident that the
guessed formula is correct. We call the number of terms used for checking the
formula the safety of the result.
. More generally, if we believe that the sequence
in question is generated by a polynomial, we can simply apply interpolation.
However, how can we know that a polynomial formula is appropriate? The
answer is quite simple: we use all but the last few terms of the sequence to
derive the formula. After this, the last terms are compared with the values
predicted by the polynomial. If they coincide, we can be confident that the
guessed formula is correct. We call the number of terms used for checking the
formula the safety of the result.
Apart from safety, the main problem we have to solve is about efficiency. For
example, maybe we would like to test whether the ![]() term
of the sequence is given by a formula of the form
term
of the sequence is given by a formula of the form
| (6) |
Thus, we need to find efficient algorithms that test for large classes of formulas. Obviously, such algorithms exist for interpolation and Pade approximation. For the present package, we implemented an efficient algorithm for a far reaching generalization of interpolation, proposed by Bernhard Beckermann and George Labahn, see FractionFreeFastGaussianElimination?. Furthermore, we show that there is also a way to guess sequences generated by Formula (6).
Using these algorithms our package clearly outperforms both Rate and GFUN,
in terms of speed as well as in the range of formulas that can be guessed.
In the following section we outline the capabilities of our package. In the Section therafter we describe the most important options that modify the behaviour of the functions.
Function Classes Suitable for Guessing
In this section we briefly present the function classes which are covered by
our package. Throughout this section, ![]() is the function we would
like to guess, and
is the function we would
like to guess, and ![]() is its generating function. The
values
is its generating function. The
values ![]() are supposed to be elements of some field
are supposed to be elements of some field ![]() , usually
the field of rationals or rational functions. We alert the reader that the
first value in the given sequence always corresponds to the value
, usually
the field of rationals or rational functions. We alert the reader that the
first value in the given sequence always corresponds to the value ![]() .
.
To load the package we type
axiom)lib RECOP FAMR2 FFFG FFFGF NEWTON UFPS UFPS1 GOPT GOPT0 GUESS GUESSINT GUESSP GUESSF1 GUESSF )library cannot find the file RECOP. )library cannot find the file FAMR2. )library cannot find the file FFFG. )library cannot find the file FFFGF. )library cannot find the file NEWTON. )library cannot find the file UFPS. )library cannot find the file UFPS1. )library cannot find the file GOPT. )library cannot find the file GOPT0. )library cannot find the file GUESS. )library cannot find the file GUESSINT. )library cannot find the file GUESSP. )library cannot find the file GUESSF1. )library cannot find the file GUESSF.
Guessing 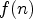
guessRecfinds recurrences of the form
where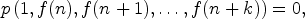
(7) 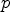 is a polynomial with coefficients in
is a polynomial with coefficients in 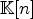 . For example,
axiomguessRec([1,1,0,1,- 1,2,- 1,5,- 4,29,- 13,854,- 685]).1.function >> Error detected within library code: Can have at most 9 scripts of each kind
. For example,
axiomguessRec([1,1,0,1,- 1,2,- 1,5,- 4,29,- 13,854,- 685]).1.function >> Error detected within library code: Can have at most 9 scripts of each kindNote that, at least in the current implementation, we do not exclude solutions that do not determine the function
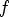 completely. For example,
given a list containing only zeros and ones, one result will be
completely. For example,
given a list containing only zeros and ones, one result will be
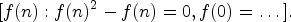
guessPReconly looks for recurrences with linear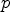 , i.e., it
recognizes P-recursive sequences. As an example,
axiomguessPRec([0, 1, 0, -1/6, 0, 1/120, 0, -1/5040, 0, 1/362880, 0, -1/39916800]).1.function >> Error detected within library code: Can have at most 9 scripts of each kind
, i.e., it
recognizes P-recursive sequences. As an example,
axiomguessPRec([0, 1, 0, -1/6, 0, 1/120, 0, -1/5040, 0, 1/362880, 0, -1/39916800]).1.function >> Error detected within library code: Can have at most 9 scripts of each kindguessRatfinds rational functions. For the sequence given in Equation (1), we find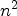 as likely solution.
as likely solution.guessExpRatfinds rational functions with an Abelian term, i.e.,
where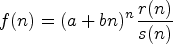
 and
and  are polynomials.
axiomguessExpRat([0,3,32,375,5184,84035]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *06guessExpRat0332375518484035] to argument(s) of type(s) PositiveInteger
are polynomials.
axiomguessExpRat([0,3,32,375,5184,84035]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *06guessExpRat0332375518484035] to argument(s) of type(s) PositiveInteger
Concerning ![]() -analogues,
-analogues, guessRec(q) finds recurrences of the
form (7), where ![]() is a polynomial with coefficients in
is a polynomial with coefficients in ![]() .
Similarly, we provide
.
Similarly, we provide ![]() -analogues for
-analogues for guessPRec and
guessRat. Finally, guessExpRat(q) recognizes functions of the form
For Sequence (5), we enter
axiomguessExpRat(q)([(1-2*q)/(1-q),1-2*q,(1-q)*(1-2*q)^3,(1-q)^2*(1-2*q)*(1-2*q-2*q^2)^3], []).1.function There are no library operations named guessExpRat Use HyperDoc Browse or issue )what op guessExpRat to learn if there is any operation containing " guessExpRat " in its name. Cannot find a definition or applicable library operation named guessExpRat with argument type(s) Variable q Perhaps you should use "@" to indicate the required return type, or "$" to specify which version of the function you need.
Guessing 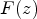
guessADEfinds an algebraic differential equation for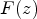 ,
i.e., an equation of the form
,
i.e., an equation of the form
where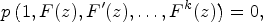
(8) 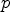 is a polynomial with coefficients in
is a polynomial with coefficients in 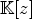 . A typical
example is
. A typical
example is 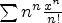 :
axiomguessADE([1,1,2,9/2,32/3,625/24,324/5,117649/720,131072/315]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *09guessADE112(/ 9 2)(/ 32 3)(/ 625 24)(/ 324 5)(/ 117649 720)(/ 131072 315)] to argument(s) of type(s) PositiveInteger
:
axiomguessADE([1,1,2,9/2,32/3,625/24,324/5,117649/720,131072/315]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *09guessADE112(/ 9 2)(/ 32 3)(/ 625 24)(/ 324 5)(/ 117649 720)(/ 131072 315)] to argument(s) of type(s) PositiveIntegerguessHoloonly looks for equations of the form (11) with linear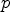 , that is, it recognizes holonomic or differentially-finite
functions. It is well known that the class of holonomic functions coincides
with the class of functions having P-recursive Taylor coefficients. However,
the number of terms necessary to find the differential equation often differs
greatly from the number of terms necessary to find the recurrence. Returning
to the example given for
, that is, it recognizes holonomic or differentially-finite
functions. It is well known that the class of holonomic functions coincides
with the class of functions having P-recursive Taylor coefficients. However,
the number of terms necessary to find the differential equation often differs
greatly from the number of terms necessary to find the recurrence. Returning
to the example given for guessPRec, we find that already the first 6 terms are sufficient to guess a generating function:axiomguessHolo([0,1,0,-1/6,0,1/120]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *06guessHolo010(/ -1 6)0(/ 1 120)] to argument(s) of type(s) PositiveIntegerMoreover, now we immediately recognise the coefficients as being those of the sine function.
guessHolois also the function provided byGFUN. Here is a comparison of average running times in seconds over several runs on the same machine for a list of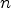 elements
elements

guessAlglooks for an algebraic equation satisfied by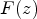 ,
i.e., an equation of the form
,
i.e., an equation of the form
the prime example being given by the Catalan numbers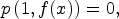 axiomguessAlg([1,1,2,5]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *04guessAlg1125] to argument(s) of type(s) PositiveInteger
axiomguessAlg([1,1,2,5]).1.function There are 1 exposed and 1 unexposed library operations named elt having 1 argument(s) but none was determined to be applicable. Use HyperDoc Browse, or issue )display op elt to learn more about the available operations. Perhaps package-calling the operation or using coercions on the arguments will allow you to apply the operation. Cannot find application of object of type OrderedVariableList [ *04guessAlg1125] to argument(s) of type(s) PositiveIntegerguessPaderecognises rational generating functions. For the Fibonacci sequence given in Equation (2), we find as likely solution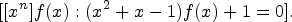
We provide ![]() -analogues, replacing differentiation with
-analogues, replacing differentiation with ![]() -dilation:
-dilation:
guessADE(q) finds differential equations of the form
| (9) |
guessHolo, guessAlg, and guessPade.
To guess a formula for Sequence (4), we enter
axiomguessRat(q)([1,1+q+q^2,(1+q+q^2)*(1+q^2),(1+q^2)*(1+q+q^2+q^3+q^4)], []).1.function There are no library operations named guessRat Use HyperDoc Browse or issue )what op guessRat to learn if there is any operation containing " guessRat " in its name. Cannot find a definition or applicable library operation named guessRat with argument type(s) Variable q Perhaps you should use "@" to indicate the required return type, or "$" to specify which version of the function you need.
Operators
The main observation made by Christian Krattenthaler in designing his program
Rate is the following: it occurs frequently that although a sequence of numbers
is not generated by a rational function, the sequence of successive quotients is.
We slightly extend upon this idea, and apply recursively one or both of the two following operators:
guessSum-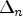 the differencing operator, transforming
the differencing operator, transforming
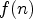 into
into 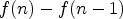 .
.guessProduct-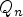 the operator that transforms
the operator that transforms 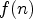 into
into
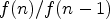 .
.
For example, to guess a formula for Sequence (3), we enter
axiomguess([0, 1, 3, 9, 33], [guessRat], [guessSum, guessProduct]).1.function There are no library operations named guess Use HyperDoc Browse or issue )what op guess to learn if there is any operation containing " guess " in its name. Cannot find a definition or applicable library operation named guess with argument type(s) List NonNegativeInteger List Variable guessRat List OrderedVariableList [guessSum,guessProduct] Perhaps you should use "@" to indicate the required return type, or "$" to specify which version of the function you need.
The second argument to guess indicates which of the functions of the
previous section to apply to each of the generated sequence, while the third
argument indicates which operators to use to generate new sequences.
In the case where only the operator ![]() is applied, our package is directly
comparable to
is applied, our package is directly
comparable to Rate. In this case the standard example is the number of
alternating sign matrices
axiomguess([1, 1, 2, 7, 42, 429, 7436, 218348], [guessRat], [guessProduct]).1.function There are no library operations named guess Use HyperDoc Browse or issue )what op guess to learn if there is any operation containing " guess " in its name. Cannot find a definition or applicable library operation named guess with argument type(s) List PositiveInteger List Variable guessRat List Variable guessProduct Perhaps you should use "@" to indicate the required return type, or "$" to specify which version of the function you need.
Here are the average running times in seconds for our package and Rate over
several runs on the same machine for a list of ![]() elements:
elements:
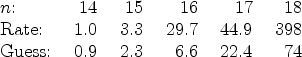 |
Options
To give you the maximum flexibility in guessing a formula for your favourite sequence, we provide options that modify the behaviour of the functions as described in Section~\ref{sec:function-classes}. The options are appended, separated by commas, to the guessing function in the form \spad{option==value}. See below for some examples.
debugspecifies whether informations about progress should be reported.safetyspecifies, as explained at the beginning of Section 2, the number of values reserved for testing any solutions found. The default setting is 1.Experiments seem to indicate that for
guessADEhigher settings are appropriate than forguessRat. I.e., if a rational function interpolates the given list of terms, where the final term is used for testing, we can be pretty sure that the formula found is correct. By contrast, we recommend settingsafetyto 3 or 4 when usingguessADE. For all algorithms exceptguessExpRatwe recommend to omit trailing zeros.onespecifies whether the guessing function should return as soon as at least one solution is found. By default, this option is set totrue.maxDegreespecifies the maximum degree of the coefficient polynomials in an algebraic differential equation or a recursion with polynomial coefficients. For rational functions with an exponential term,maxDegreebounds the degree of the denominator polynomial. This option is especially interesting if trying rather long sequences where it is unclear whether a solution will be found or not. SettingmaxDegreeto -1, which is the default, specifies that the maximum degree can be arbitrary.allDegreesspecifies whether all possibilities of the degree vector - taking into accountmaxDegree- should be tried. The default istrueforguessPadeandguessRatandfalsefor all other functions.homogeneousspecifies whether the search space should be restricted to homogeneous algebraic differential equations or homogeneous recurrences. By default, it is set tofalse.maxDerivative-maxShiftspecify the maximum derivative in an algebraic differential equation, or, in a recurrence relation, the maximum shift. Setting the option to -1 specifies that the maximum derivative - the maximum shift - may be arbitrary.maxPowerspecifies the maximum total degree in an algebraic differential equation or recurrence: for example, the degree of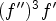 is 4. Setting the option to -1 specifies that the maximum total degree
may be arbitrary. For example,
axioml := [1, 1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, 126742987, 1687054711, 47301104551, 1123424582771, 32606721084786, 1662315215971057];Type: List PositiveInteger?axiomguessRec(l, maxPower==2).1.function There are no library operations named maxPower Use HyperDoc Browse or issue )what op maxPower to learn if there is any operation containing " maxPower " in its name. Cannot find a definition or applicable library operation named maxPower with argument type(s) PositiveInteger Perhaps you should use "@" to indicate the required return type, or "$" to specify which version of the function you need.
is 4. Setting the option to -1 specifies that the maximum total degree
may be arbitrary. For example,
axioml := [1, 1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, 126742987, 1687054711, 47301104551, 1123424582771, 32606721084786, 1662315215971057];Type: List PositiveInteger?axiomguessRec(l, maxPower==2).1.function There are no library operations named maxPower Use HyperDoc Browse or issue )what op maxPower to learn if there is any operation containing " maxPower " in its name. Cannot find a definition or applicable library operation named maxPower with argument type(s) PositiveInteger Perhaps you should use "@" to indicate the required return type, or "$" to specify which version of the function you need.returns the Somos-4 recurrence, whereas without limiting the power to 2, we need the first 33 values, and instead of roughly one second half a minute of computing time.
maxLevelspecifies how many levels of recursion are tried when applying operators. Note that, applying either of the two operators results in a sequence which is by one shorter than the original sequence. Therefore, in case bothguessSumandguessProductare specified, the number of times a guessing algorithm from the given list of functions is applied is roughly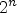 , where
, where
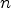 is the number of terms in the given sequence. Thus, especially when the
list of terms is long, it is important to set
is the number of terms in the given sequence. Thus, especially when the
list of terms is long, it is important to set maxLevelto a low value.Still, the default value is -1, which means that the number of levels is only restricted by the number of terms given in the sequence.
indexName,variableName,functionNamespecify symbols to be used for the output. The defaults aren,xandfrespectively.
A note on the output
The output of any function described in Section 3 is a list of formulae which seem to fit, along with an integer that states from which term on the formula is correct. The latter is necessary, because rational interpolation features sometimes unattainable points, as the following example shows:
axiomguessRat([3, 4, 7/2, 18/5, 11/3, 26/7])
| (10) |
![]() indicates that the first two terms of the sequence might not
coincide with the value predicted by the returned function. A similar situation
occurs, if the function generating the sequence has a singular point at
indicates that the first two terms of the sequence might not
coincide with the value predicted by the returned function. A similar situation
occurs, if the function generating the sequence has a singular point at
![]() , where
, where ![]() and
and ![]() is the number of given
values. We would like to stress that this is rather a feature than a
bug: most terms will be correct, just as in the example above, where the
value at
is the number of given
values. We would like to stress that this is rather a feature than a
bug: most terms will be correct, just as in the example above, where the
value at ![]() is indeed 3.
is indeed 3.