Goal: To explore the issues and develop tools for implementing IndexedUnion, a new domain constructor proposed by William Sit.
Discussion: The idea of creating a new domain IndexedUnion in Axiom grows out of a discussion on whether the current Union, a primitive type that allows two versions, tagged and untagged, should be generalized to allow a mixed tagged/untagged version. The current implementation specifies that in the tagged version, the tags must be distinct, while in the untagged version, all domains forming the union must be distinct. The compiler does not enforce these restrictions. Also, in the tagged case, the exported functions that construct elements from component domains have identical signatures if the domains are the same, making it only possible to create elements from the first of such identical domains.
fricas
)show Union(a:Integer, b:Integer)
Union(a: Integer,b: Integer) is a domain constructor.
------------------------------- Operations --------------------------------
?=? : (%,%) -> Boolean ?case? : (%,a) -> Boolean
?case? : (%,b) -> Boolean coerce : % -> OutputForm
construct : Integer -> % construct : Integer -> %
?.? : (%,a) -> Integer ?.? : (%,b) -> Integer
?~=? : (%,%) -> Boolean
Notice that there are two construct: Integer->%. The proposed IndexedUnion domain will be more general, and will avoid such problems. Unfortunately, there are a number of hurdles and an examination of these gives insight into the original design.
Contributors: Ralf Hemmecke, Bill Page, William Sit, Stephen Wilson (feel free to add yours; this page is open source)
The construction of Union (in Axiom) as implementing the notion of coproduct or external direct sum in Category Theory,
specifically as disjoint union in Set Theory and taking place in the category of sets, should have nothing to do with tags, but with an
index set and the sets associated with the indices. The notions of union, coproduct, and colimit are distinct concepts in
category theory, but let's not get too involved with these for the time being. Since in Axiom, sets are domains of SetCategory, and an indexed family of sets is really a mapping from the indexed set to the category of sets, accordingly, it is proposed to create an alternative:
IndexedUnion(I: SetCategory, g:I -> SetCategory):SetCategory
Example 1:
I:= Integer
g(i:I):SetCategory == if even? i then Integer else String
J:= IndexedUnion(I,g)
A more mathematical example would be to construct the prime field if i is prime, and a product of prime fields over distinct prime factors of i if i is
composite. The disjoint union of 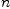 copies of
copies of 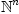 can be used to represent all partial derivatives of
can be used to represent all partial derivatives of 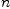 dependent functions with respect to
dependent functions with respect to 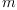 independent variables. In the next example, we construct the set of all square matrices with integer entries:
independent variables. In the next example, we construct the set of all square matrices with integer entries:
Example 2:
I:=PositiveInteger
g(i:I):SetCategory == SquareMatrix(i, Integer)
J:=IndexedUnion(i,g)
Technically, g here is a domain constructor. Whether the implementation should be done as primitive or not depends on the language
limitation of Spad. As we shall see, at the Spad level, we would need domains and categories to be first class objects and maps
would need to allow input-dependent types as its output. So Axiom may not allow that.
As it currently exists, Union (in Axiom) can form the disjoint union of a finite number of sets (each of which is a domain of
SetCategory, NOT a finite set of elements in Set S for some domain S). The index set in the tagged version is
the set of tags, but this is clearly not enough (there being no useful operations in the set of tags). The index set in the untagged
version probably defaults to 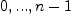 where
where 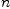 is the number of sets (domains) in the union, counted with multiplicities.
is the number of sets (domains) in the union, counted with multiplicities. Union is a primitive type and its code lives below the algebra level; apparently, Rep for Union is of the form (i.x) where i is an integer ranging from 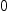 to
to 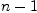 and
and x is the value in the domain from the 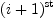 argument of
argument of Union. This is independent of whether the domains are tagged or not. The tags seem to live in hard-coded signatures of exports when the domain is instantiated. For example:
fricas
)show Union(a:Integer, b:String)
Union(a: Integer,b: String) is a domain constructor.
------------------------------- Operations --------------------------------
?=? : (%,%) -> Boolean ?case? : (%,a) -> Boolean
?case? : (%,b) -> Boolean coerce : % -> OutputForm
construct : Integer -> % construct : String -> %
?.? : (%,a) -> Integer ?.? : (%,b) -> String
?~=? : (%,%) -> Boolean
We already noted the two construct (here they are distinguishable, but a clumsy way if there are more domains than two). One important thing to note, however, is the signature for two case and the dot functions.
These signatures in tagged Union are outrageous (abuse of language)! Neither identifier a
nor identifier b is a domain! The implementers again finessed the difficult problems because they are working below the algebra layer. They are more pragmatic than you think and suggest that the implementation for IndexedUnion most likely would have to be abusing the language too. As long as one can be abusing the language (or rather, there is no language to abuse at pre-algebra time!), why not distinguish the two construct also by a and b (instead of just by the domains, which could be identical)? Something like:
construct: (Integer, a) -> %
construct: (Integer, b) -> %
Note here that the tags a and b are local and not entirely accessible! The tags may be shadowed by a global variable of the same name. The following example shows the poor design of the exported functions in tagged Union (there are also problems with the untagged Union, you can find out the problems as an exercise).
fricas
test:= Union(a:String, b:String)
Type: Type
fricas
c:test:="abc"
Type: Union(a: String,b: String,...)
fricas
c case b
Type: Boolean
fricas
-- c.b would fail with an error
b:Integer:=3
Type: Integer
fricas
c case b
Type: Boolean
fricas
c.b
Type: Character
fricas
c case a
Type: Boolean
fricas
c.a
Type: String
fricas
a:String:="d"
Type: String
fricas
c case a
Type: Boolean
fricas
c.a
Type: String
The convenience of tags (in the case of a small, finite index set) is that the user does not have to make the set of tags into a
domain (as required to become the source for the function g) and the tags are supposedly more meaningful to the user. Now, is a hybrid Union type desirable? Example 6 below will illustrate a possible use.
The "mixed" Union where tags are allowed for a small finite subset of the index set would allow the best of both
worlds. Unfortunately, tags are identifiers (that is, symbols or effectively, strings, almost by definition) whereas there is no such restriction on an index set (or the rest of it). In most
cases, for the index set to remain a domain, the indices must be homogeneous in type and so if there are tags, then the index set
should be a subset of the set of all strings. In the finite case, it would be an element of Set String (and thus, not a domain of SetCategory). But Union should allow infinite index sets as well and an infinite set of strings is difficult to manipulate in code.
One plausible reason why Union is implemented as a primitive rather than at the algebra level is to avoid having to require a user at
the algebra level to make the index set into a domain. To allow a hybrid index set, it would be again simpler to implement as a
primitive than at the algebra level, because requiring the user to make the hybrid index set into a domain
would be a bit harder and less intuitive. This, however, can be done. We need a domain constructor:
TagsAsDomain( T: Set String): SetCategory
Note that Set String is used, not List String (to avoid duplicates). This type of construction is already used in Axiom, as in the domain "failed" when we
use Union("failed", ...). So it is probably handled specifically by the compiler, or there is a similar function at lower level. The above
specification would enforce automatically the constraints Spad is currently specifying: In untagged Union, the domains must be distinct. In tagged Union, the tags must be distinct:
Example 3:
I:= TagsAsDomain({"a", "b", "c"})
-- this would be {"a","b","c"} as a domain
g(i:I):SetCategory ==
i = "a" => A
i = "b" => B
i = "c" => C
J:=IndexedUnion(I,g)
Clearly this is a bit awkward at the algebra level, compared to:
Union(a:A, b:B, c:C)
But a compiler can easily translate the above into the detailed algebra code in Example 3. On the other hand, in this algebraic level
version, there is no "untagged" Union (all domains in IndexedUnion are indexed) and the "untagged" version should not require any
constraints such as the associated domains be distinct. It is only required that the elements of the index set be distinct, which is
automatically enforced because it is a set. Indeed, hybrid union indexed by a heterogeneous set can be handled easily too, using
IndexedUnion itself:
Example 4:
I:=IntegerMod(2)
L:=TagsAsDomain({"a","b","c"})
g(i:I):SetCategory ==
zero? i => L
IntegerMod(5)
J:= IndexedUnion(I,g)
f(j:J):SetCategory == ...
K:= IndexedUnion(J, f)
Again, it would be much easier to have this implemented enumeratively and perhaps as a primitive and allow the user to simply
write, in case the index set is finite and small:
Union(a:A,b:B,c:C,D,E,F,G,H)
However, the more abstract specification of IndexedUnion is far more powerful:
Example 5:
I:=IntegerMod(2)
L:=TagsAsDomain({"a","b","c"})
g(i:I):SetCategory ==
zero? i => L
String
J:= IndexedUnion(I,g)
f(j:J):SetCategory == ...
K:= IndexedUnion(J, f)
In the definition of f, we can actually distinguish the "a" in L from the "a" in String because each element of IndexedUnion is
"tagged" and we will use the "=" from L or from String (this is related to the scoping issue of current implementation raised by
Gaby). Since J in Example 5 is itself an IndexedUnion object, this brings us to the "case" question, or more generally:
What should be exported from IndexedUnion?
Clearly, there needs to be a way to coerce elements from the domains into the union. If we were to adopt Bill Page's idea that the
injections (and projections for Product or Record) should be named by tags, then it would be very clumsy to implement them when
the Union is over a large finite set and impossible over an infinite set. This may be one reason why Axiom separates Union into two
versions, tagged (when the indexed set is finite and small) and untagged (the general case). There are only two purposes of
tags: (1) to distinguish cases when a domain occurs multiple times in the arguments of Union, and (2) for convenience of use. The
first of these can be handled by the index set and the second, too, but convenience depends on the size of the index set, as
illustrated in the previous examples.
Based on the notion of constructing IndexedUnion using an index set, and the poor handling of tags in the current implementation for Union, the following exports are proposed (there should be more if one
compares this with IndexedAggregate or other Indexed* constructors; they may be important in terms of implementation, for example, hash functions for managing memory usage):
IndexedUnion(I: SetCategory, g:I ->SetCategory):SetCategory == with
"=": (%, %) -> Boolean
index: % -> I
++ index(x) returns the index i such that x belongs to g(i)
value(x:%): g(index(x))
++ index(x) returns x as an element in g(index(x))
coerce(i:I, x:g(i)): %
++ coerce(i,x) creates x as an element of % in the component g(i)
These are just generalization of what currently exist but notice case is removed and replaced by index and value. Instead of
multiple overloading of case and coerce, we now need only one (this afterall, is exactly the advantage of indexing over explicit
enumeration). Of course, we need to be able to use input-dependent signatures. This is a requirement when we deal with
heterogeneous objects. In Example 5, where J itself is defined using IndexedUnion, the function f may be defined in the following
way. The example illustrates how IndexedUnion may be used:
Example 6 (Example 5 continued):
I:=IntegerMod(2)
L:=tagsAsDomain({"a","b","c"})
g(i:I):SetCategory ==
zero? i => L
String
J:= IndexedUnion(I,g)
f(j, J) :SetCategory ==
jU := value(j)
index(j) =$I 0 =>
jU =$L "a" => A
jU =$L "b" => B
jU =$L "c" => C
IntegerMod(#jU)
K:=IndexedUnion(J,f)
Of course this example is contrived. However, one can imagine constructions in mathematics over a set J where for a finite number of
(exception) elements of J, there are two cases whereas for every other there is only one. This would necessitate exceptional
handling as in Example 6 above.
What about the data representation of IndexedUnion? Can we do this at the algebra level? We seem to need non-homogeneous data
representation! In lower level, this is not difficult, say using pointers (perhaps another reason why Union is implemented as
primitive, to hide pointers at the algebra level), but at the algebra level, Axiom is not designed for heterogeneous objects (that's why
people use C++). A plausible representation (which is just like (i.x) discussed earlier) is:
Rep:= Record( index: I, value:g(i) )
if allowed at the algebra level, would be perfect. (Note that Record, categorically the
product construction, should also be done using an index set.) A plausible and trivial implementation of the exported functions is:
x = y == (x.index = y.index) and (x.value = y.value)
index(x) == x.index
value(x)== x.value
coerce(i:I, v:g(i)) == [i, v]$Rep
By generalizing TagsAsDomain, replacing String by any domain, we can create arbitrarily complicated index sets to use in IndexedUnion.
Below, we have test code to implement Domain (but called MyDomain to avoid possible confusion with the actual Domain) and for ListAsDomain SetAsDomain and StreamAsDomain. To facilitate discussion, line references are in-lined as comments::
fricas
)abbrev domain MYDOM MyDomain
++ Author: William Sit
++ Date Created: July 15, 2007
++ Description: This domain attempts to be the Domain of all domains
++ to allow for construction such as Union which are based on an index set.
++ The family of domains can then be specified by a map from the index
++ set to this domain. The domain is needed in order for a list of domains
++ (even finite) to be typed.
-- *** Warning: Design may change and limitation in use applies.
MyDomain():Spec == Imp where -- 1
Spec == Join(SetCategory, CoercibleTo(OutputForm)) with -- 2
coerce: String -> % -- 3
coerce: SExpression -> % -- 4
Imp == add -- 5
Rep:= SExpression -- 6
x = y == (x@Rep) = (y@Rep) -- 7
coerce(x:%):OutputForm == x@Rep pretend OutputForm -- 8
coerce(x:String):% == convert(x::Symbol)$Rep pretend % -- 9
coerce(x:SExpression):% == x pretend % --10
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/2070302996248901361-25px.004.spad
using old system compiler.
MYDOM abbreviates domain MyDomain
------------------------------------------------------------------------
initializing NRLIB MYDOM for MyDomain
compiling into NRLIB MYDOM
compiling exported = : ($,$) -> Boolean
Time: 0 SEC.
compiling exported coerce : $ -> OutputForm
MYDOM;coerce;$Of;2 is replaced by x
Time: 0 SEC.
compiling exported coerce : String -> $
Time: 0 SEC.
compiling exported coerce : SExpression -> $
MYDOM;coerce;Se$;4 is replaced by x
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |MyDomain| REDEFINED
;;; *** |MyDomain| REDEFINED
Time: 0 SEC.
Warnings:
[1] coerce: pretend$ -- should replace by @
Cumulative Statistics for Constructor MyDomain
Time: 0 seconds
finalizing NRLIB MYDOM
Processing MyDomain for Browser database:
--------constructor---------
--->-->MyDomain((coerce (% (String)))): Not documented!!!!
--->-->MyDomain((coerce (% (SExpression)))): Not documented!!!!
; compiling file "/var/aw/var/LatexWiki/MYDOM.NRLIB/MYDOM.lsp" (written 31 JUL 2013 03:13:32 PM):
; /var/aw/var/LatexWiki/MYDOM.NRLIB/MYDOM.fasl written
; compilation finished in 0:00:00.016
------------------------------------------------------------------------
MyDomain is now explicitly exposed in frame initial
MyDomain will be automatically loaded when needed from
/var/aw/var/LatexWiki/MYDOM.NRLIB/MYDOMWe declared MyDomain as a domain constructor (line 1) when it may be argued that a category constructor is more appropriate. But we are only in the exploration stage. The crash that we shall see may be due to this though. We intend objects in this domain will be constructed from String (line 3) or SExpression (line 4), such as "Integer" (String) or (Integer) (SExpression). We use SExpression for data representation because at this time, we don't know what better domain to use! We already anticipate difficulty ahead (at least at the algebra level) to turn an SExpression into an actual domain. There are differences.
fricas
)clear all
All user variables and function definitions have been cleared.
p:=POLY FRAC INT
Type: Type
fricas
a:p:= 2*x+1
Type: Polynomial(Fraction(Integer))
fricas
q:=dom(sample()$p)
fricas
b:q:= 2*x + 1
Type: Polynomial(Integer)
Here p is a genuine domain whereas its SExpression q is simply a nested list of lisp symbols. We need to be able to turn an SExpression
into a genuine domain.
In line 8, pretend has to be used. The alternatives:
(coerce(x@Rep)@OutputForm)$SExpression
coerce(x@Rep)$Expression
both did compile. However, the following run-time command crashed Axiom:
a:="Integer"::MyDomain
In line 9, x::Symbol is used because this is how say Integer appears in 'SEX'::
fricas
c:=dom(sample()$Integer)
fricas
symbol?(car c)
Type: Boolean
Warning: x::Symbol only works for a domain defined with one identifier.
It would not make sense for domain constructors with parameters like "SQMATRIX(5, FRAC INT)".
The SExpression is a list of the form (f x1 x2 ...) where f is
the constructor and x1, x2 are parameters for f, recursively repressented using the same
format; constants are either elements of Integer, such as 5, or of Float or of String.
fricas
d:=dom(sample()$SQMATRIX(5,FRAC INT))
This brings up two problems: We will need some type of parser to take a string like
"SQMATRIX(5,INT) into its SExpression and we need to expand abbreviations. Replacing line 9 by:
coerce(x:String):% == (convert(x)$SExpression) pretend %
did not work, even when the string x looked like the SExpression (as nested list of lisp symbols). This was because x remained
a string, which is an atom in SExpression.
The domain constructor ListAsDomain generalizes the hypothetical TagsAsDomain discussed earlier. As noted earlier, lines 8-12 are needed because coerce to OutputForm does not work for SExpression.
fricas
)abbrev domain LDOMAIN ListAsDomain
++ Author: William Sit
++ Date Created: July 15, 2007
++ Description: This domain is needed to enable mappings from finite lists
++ to other finite lists. Maps in Axiom need source and target domains.
++ Axiom currently allows constructions of finite lists, but only as
++ objects in a domain, not as a domain itself. This domain lifts such lists
++ into a domain.
ListAsDomain(S:SetCategory, T: List S): Spec == Imp where -- 1
Spec == Join(SetCategory, CoercibleTo(S), CoercibleTo(OutputForm)) with -- 2
coerce: S-> % -- 3
Imp == add -- 4
Rep:= S -- 5
x = y == (x@Rep) = (y@Rep) -- 6
coerce(x:%):S == x@Rep -- 7
coerce(x:%):OutputForm == -- 8
if S is SExpression then -- 9
x@Rep pretend OutputForm --10
else --11
(coerce(x@Rep)@OutputForm)$S --12
coerce(x:S) == --13
not member?(x, T) => error "not an element of domain" --14
x pretend % --15
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/602997873054000130-25px.008.spad
using old system compiler.
LDOMAIN abbreviates domain ListAsDomain
(parseTran op ~= u (elt S @) @)
------------------------------------------------------------------------
initializing NRLIB LDOMAIN for ListAsDomain
compiling into NRLIB LDOMAIN
****** Domain: S already in scope
compiling exported = : ($,$) -> Boolean
Time: 0 SEC.
compiling exported coerce : $ -> S
LDOMAIN;coerce;$S;2 is replaced by x
Time: 0 SEC.
compiling exported coerce : $ -> OutputForm
Time: 0 SEC.
compiling exported coerce : S -> $
Time: 0.01 SEC.
(time taken in buildFunctor: 0)
;;; *** |ListAsDomain| REDEFINED
;;; *** |ListAsDomain| REDEFINED
Time: 0.01 SEC.
Warnings:
[1] coerce: pretend$ -- should replace by @
Cumulative Statistics for Constructor ListAsDomain
Time: 0.02 seconds
finalizing NRLIB LDOMAIN
Processing ListAsDomain for Browser database:
--------constructor---------
--->-->ListAsDomain((coerce (% S))): Not documented!!!!
; compiling file "/var/aw/var/LatexWiki/LDOMAIN.NRLIB/LDOMAIN.lsp" (written 31 JUL 2013 03:13:32 PM):
; /var/aw/var/LatexWiki/LDOMAIN.NRLIB/LDOMAIN.fasl written
; compilation finished in 0:00:00.016
------------------------------------------------------------------------
ListAsDomain is now explicitly exposed in frame initial
ListAsDomain will be automatically loaded when needed from
/var/aw/var/LatexWiki/LDOMAIN.NRLIB/LDOMAINHere is a sample illustration.
fricas
)clear all
All user variables and function definitions have been cleared.
a:="Integer"::MyDomain
fricas
b:="String"::MyDomain
fricas
p:=ListAsDomain(MyDomain, [a,b])
Type: Type
fricas
q:=ListAsDomain(Integer, [1,2,3])
Type: Type
fricas
1::q
Type: ListAsDomain
?(Integer,
[1,
2,
3])
fricas
g(i:q):q == (if ((i::Integer)) = 2 then (3::q) else (1::q))
Function declaration g : ListAsDomain(Integer,[1,2,3]) ->
ListAsDomain(Integer,[1,2,3]) has been added to workspace.
Type: Void
fricas
[g(1), g(2), g(3)]
fricas
Compiling function g with type ListAsDomain(Integer,[1,2,3]) ->
ListAsDomain(Integer,[1,2,3])
Type: List(ListAsDomain
?(Integer,
[1,
2,
3]))
fricas
g(4)
>> Error detected within library code:
not an element of domain
Note that in the line defining q, a cannot be used instead of Integer because a is really not a domain.
Unfortunately, while q works, p does not, since a::p will crash Axiom! Don't know why yet.
Warning: Here the map g is not a domain constructor as specified for IndexedUnion. This could be the source of the crash here and the one mentioned later when SetAsDomain is used.
fricas
)abbrev domain SDOMAIN SetAsDomain
++ Author: William Sit
++ Date Created: July 15, 2007
++ Description: This domain is needed to enable mappings from finite sets
++ to other finite sets. Maps in Axiom needs source and target domains.
++ Axiom currently allows constructions of finite sets, but only as
++ objects in a domain, not as a domain itself. This domain lifts such sets
++ into a domain.
SetAsDomain(S:SetCategory, T: Set S): Spec == Imp where -- 1
Spec == Join(SetCategory, CoercibleTo(S), CoercibleTo(OutputForm)) with -- 2
coerce: S-> % -- 3
Imp == add -- 4
Rep:= S -- 5
x = y == (x@Rep) = (y@Rep) -- 6
coerce(x:%):S == x@Rep -- 7
coerce(x:%):OutputForm == -- 8
if S is SExpression then -- 9
x@Rep pretend OutputForm --10
else --11
(coerce(x@Rep)@OutputForm)$S --12
coerce(x:S) == --13
not member?(x, T) => error "not an element of domain" --14
x pretend % --15
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/490466365863101861-25px.010.spad
using old system compiler.
SDOMAIN abbreviates domain SetAsDomain
(parseTran op ~= u (elt S @) @)
------------------------------------------------------------------------
initializing NRLIB SDOMAIN for SetAsDomain
compiling into NRLIB SDOMAIN
compiling exported = : ($,$) -> Boolean
Time: 0 SEC.
compiling exported coerce : $ -> S
SDOMAIN;coerce;$S;2 is replaced by x
Time: 0 SEC.
compiling exported coerce : $ -> OutputForm
Time: 0 SEC.
compiling exported coerce : S -> $
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |SetAsDomain| REDEFINED
;;; *** |SetAsDomain| REDEFINED
Time: 0 SEC.
Warnings:
[1] coerce: pretend$ -- should replace by @
Cumulative Statistics for Constructor SetAsDomain
Time: 0 seconds
finalizing NRLIB SDOMAIN
Processing SetAsDomain for Browser database:
--------constructor---------
--->-->SetAsDomain((coerce (% S))): Not documented!!!!
; compiling file "/var/aw/var/LatexWiki/SDOMAIN.NRLIB/SDOMAIN.lsp" (written 31 JUL 2013 03:13:32 PM):
; /var/aw/var/LatexWiki/SDOMAIN.NRLIB/SDOMAIN.fasl written
; compilation finished in 0:00:00.016
------------------------------------------------------------------------
SetAsDomain is now explicitly exposed in frame initial
SetAsDomain will be automatically loaded when needed from
/var/aw/var/LatexWiki/SDOMAIN.NRLIB/SDOMAINThere is little difference in terms of the code for ListAsDomain and SetAsDomain. However, ListAsDomain is more general than SetAsDomain in the sense that the indices need not be distinct. One may wonder why that might be useful. Suppose we want to create the set of IntegerMod(n) where n is a certain sequence defined by a formula 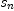 where
where 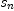 need not be distinct. One can use the natural numbers to index, but then we miss the fact that some of objects are equal. Anyway, it is convenient to use
need not be distinct. One can use the natural numbers to index, but then we miss the fact that some of objects are equal. Anyway, it is convenient to use List instead of Set (Axiom has many examples where Set should have been used but List is used instead.) While we are at it, we might as well also allow StreamAsDomain as long as things are finite. The finiteness condition is required because we want to make sure that set of objects included in the domain is exactly the given set, list, or stream. If we trust the user, we do not need to test for membership in line 14.
Known Problem: The above does not work with SetAsDomain, not even::
fricas
r:=SetAsDomain(Integer, brace{[1,2,3]})
Type: Type
The next line will crash or go into infinite loop:
1::r -- crashes, goes into infinite loop
Can anyone help find the problem?
fricas
)abbrev domain STDOMAIN StreamAsDomain
++ Author: William Sit
++ Date Created: July 15, 2007
++ Description: This domain is needed to enable mappings from finite streams
++ to other finite streams. Maps in Axiom need source and target domains.
++ Axiom currently allows constructions of finite streams, but only as
++ objects in a domain, not as a domain itself. This domain lifts such streams
++ into a domain.
-- requires that Stream S has finiteAggregate in order to use member?
StreamAsDomain(S:SetCategory, T: Stream S): Spec == Imp where
Spec == Join(SetCategory, CoercibleTo(S), CoercibleTo(OutputForm)) with
if Stream S has finiteAggregate then coerce: S-> %
Imp == add
Rep:= S
x = y == (x@Rep) = (y@Rep)
coerce(x:%):S == x@Rep
coerce(x:%):OutputForm ==
if S is SExpression then
x@Rep pretend OutputForm
else
(coerce(x@Rep)@OutputForm)$S
if Stream S has finiteAggregate then
coerce(x:S) ==
not member?(x, T) => error "not an element of domain"
x::%
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/7839692708683314954-25px.012.spad
using old system compiler.
STDOMAIN abbreviates domain StreamAsDomain
(parseTran op ~= u (elt S @) @)
------------------------------------------------------------------------
initializing NRLIB STDOMAIN for StreamAsDomain
compiling into NRLIB STDOMAIN
compiling exported = : ($,$) -> Boolean
Time: 0.01 SEC.
compiling exported coerce : $ -> S
STDOMAIN;coerce;$S;2 is replaced by x
Time: 0 SEC.
compiling exported coerce : $ -> OutputForm
Time: 0 SEC.
****** Domain: (Stream S) already in scope
augmenting (Stream S): (finiteAggregate)
augmenting $: (SIGNATURE $ coerce ($ S))
compiling exported coerce : S -> $
Time: 0 SEC.
****** Domain: (Stream S) already in scope
augmenting (Stream S): (finiteAggregate)
augmenting $: (SIGNATURE $ coerce ($ S))
(time taken in buildFunctor: 0)
;;; *** |StreamAsDomain| REDEFINED
;;; *** |StreamAsDomain| REDEFINED
Time: 0 SEC.
Cumulative Statistics for Constructor StreamAsDomain
Time: 0.01 seconds
finalizing NRLIB STDOMAIN
Processing StreamAsDomain for Browser database:
--------constructor---------
--->-->StreamAsDomain((coerce (% S))): Not documented!!!!
; compiling file "/var/aw/var/LatexWiki/STDOMAIN.NRLIB/STDOMAIN.lsp" (written 31 JUL 2013 03:13:32 PM):
; /var/aw/var/LatexWiki/STDOMAIN.NRLIB/STDOMAIN.fasl written
; compilation finished in 0:00:00.018
------------------------------------------------------------------------
StreamAsDomain is now explicitly exposed in frame initial
StreamAsDomain will be automatically loaded when needed from
/var/aw/var/LatexWiki/STDOMAIN.NRLIB/STDOMAIN