I am trying to create formulae for products with, say, p sub k as
symbols. These are the results from two, at least naively identical formulae:
fricas
(1+p[1])*(1+p[2])
Type: Polynomial(Integer)
fricas
product(1+p[k],k=1..2)
Type: Expression(Integer)
But perhaps unexpectedly, the 2nd command is interpreted as just 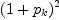 .
.
How could one use "product" (or "sum" for that reason) and an indexed way to
denote variables?
--------------
In FriCAS product denotes the formal product and in this example is
looking for an expression involving the variable k. For example:
fricas
product(sin(k),k=1..3)
Type: Expression(Integer)
But despite appearances the symbol 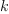 in
in ![p[k] p[k]](images/7930660265814618255-16.0px.png) in the previous command
is not what FriCAS considers a variable. In FriCAS
in the previous command
is not what FriCAS considers a variable. In FriCAS ![p[k] p[k]](images/7930660265814618255-16.0px.png) is assumed to be
of type symbol,
is assumed to be
of type symbol, 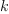 is assumed to be a variable but variables can be coerced
to be a symbol. Only variables can be assigned values but any symbol can
"stand for" unknown values in expressions.
is assumed to be a variable but variables can be coerced
to be a symbol. Only variables can be assigned values but any symbol can
"stand for" unknown values in expressions.
fricas
p[k]
Type: Symbol
fricas
1+p[k]
Type: Polynomial(Integer)
fricas
p[k]:=1
The form on the left hand side of an assignment must be a single
variable, a Tuple of variables or a reference to an entry in an
object supporting the setelt operation.
Understanding this distinction is somethimes important to understand why
FriCAS does what it does. ![1+p[k] 1+p[k]](images/1833733765201133929-16.0px.png) is assumed to be a polynomial over
is assumed to be a polynomial over ![p[k] p[k]](images/7930660265814618255-16.0px.png) not
not 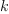 .
.
In fact, much more complicated indexed symbols can be created in FriCAS. For
example
fricas
P ==> script(p,[[a,b],[c],[d],[e]])
Type: Void
fricas
reduce(+, [P for a in 1..3])
Type: Polynomial(Integer)
Within this MathAction FriCAS wiki it is also possible to create
symbols that will be displayed as superscripted or subscripted
variables which can be assigned values. In fact any LaTeX symbol
can be generated by using the underscore charact to "protect"
special charactes such as \. For example
fricas
Q:=p_^_\alpha___\beta
Type: Variable(p^\alpha_\beta)
fricas
1+Q
Type: Polynomial(Integer)
In the above the first underscore protects the second underscore which is
then handled by LaTeX as the beginning of a subscript and next underscore
protects the \ which begins a Greek letter, etc. FriCAS treats the entire
thing as a long variable name. Note however that this only
works here and not within stand alone FriCAS.
Probably what you should write is
fricas
reduce(*,[1+p[k] for k in 1..2])
Type: Polynomial(Integer)
Here the operation of for, creating a sequence, does not treat:
1+p[k]
as a polynomial over ![p[k] p[k]](images/7930660265814618255-16.0px.png) but the final result is a polynomial.
but the final result is a polynomial.
The same comments apply to sum() which represents a formal sum.
Alternatively, and more generally, one can use BasicOperator?
fricas
p:=operator 'p
fricas
p(1)
Type: Expression(Integer)
fricas
p(k)
Type: Expression(Integer)
fricas
product(1+p(k),k=1..2)
Type: Expression(Integer)
You can attach a display property so that the argument to p appears as a subscript
fricas
displayOfp(l:List OUTFORM):OUTFORM == subscript('p,l)
Function declaration displayOfp : List(OutputForm) -> OutputForm has
been added to workspace.
Type: Void
fricas
display(p,displayOfp)
fricas
Compiling function displayOfp with type List(OutputForm) ->
OutputFormfricas
product(1+p(k),k=1..2)
Type: Expression(Integer)
You can also attach an evaluation property to handle particular values of the argument
fricas
evalOfp(a:EXPR INT):EXPR INT == {one? a => 1 ; kernel(p,a)}
Function declaration evalOfp : Expression(Integer) -> Expression(
Integer) has been added to workspace.
Type: Void
fricas
evaluate(p,evalOfp)
fricas
Compiling function evalOfp with type Expression(Integer) ->
Expression(Integer)fricas
[p 1,p 2, p k]
Type: List(Expression(Integer))
fricas
product(1+p(k),k=1..2)
Type: Expression(Integer)
This is related:
fricas
l:=[1,2,4,8,16]
Type: List(PositiveInteger
?)
fricas
sum(l.(1+2*k),k=0..2)
There are no library operations named l
Use HyperDoc Browse or issue
)what op l
to learn if there is any operation containing " l " in its name.
Cannot find a definition or applicable library operation named l
with argument type(s)
Polynomial(Integer)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
![]() .
.![]() in
in ![]() in the previous command
is not what FriCAS considers a variable. In FriCAS
in the previous command
is not what FriCAS considers a variable. In FriCAS ![]() is assumed to be
of type symbol,
is assumed to be
of type symbol, ![]() is assumed to be a variable but variables can be coerced
to be a symbol. Only variables can be assigned values but any symbol can
"stand for" unknown values in expressions.
is assumed to be a variable but variables can be coerced
to be a symbol. Only variables can be assigned values but any symbol can
"stand for" unknown values in expressions.![]() is assumed to be a polynomial over
is assumed to be a polynomial over ![]() not
not ![]() .
.![]() but the final result is a polynomial.
but the final result is a polynomial.