References to Morton codes (also known as z-order and Lebesgue curves):

• http://www.codexon.com/posts/morton-codes
• http://en.wikipedia.org/wiki/Z-order_%28curve%29
• http://www.cs.umd.edu/~hjs/pubs/bulkload.pdf
• http://graphics.stanford.edu/~seander/bithacks.html#InterleaveBMN
• http://stackoverflow.com/questions/1024754/how-to-compute-a-3d-morton-number-interleave-the-bits-of-3-ints
• http://www.mathcurve.com/fractals/lebesgue/lebesgue.shtml

-- i'th group of n bits of h
bits(h,n,i) == And(mask n,shift(h,-n*i))

Type: Void

-- mix groups of n bits of h with groups of m bits of k
morton(h,n,k,m) ==
 r:SingleInteger:=0
 if n+m > 0 then
   i:=0
   -- stop before fixnum overflow
   while (i+1)*(n+m) <= 29 repeat
     mix:=Or(shift(bits(h,n,i),m),bits(k,m,i))
     r:=Or(r,shift(mix,i*(n+m)))
     i:=i+1
 r

Type: Void

listHash(l) ==
 r:SingleInteger:=0
 i:=0
 while not empty?(l) repeat
   -- equalize hash weight by number of elements
   r:=morton(r,i,hash first l,1)
   l:=rest l
   i:=i+1
 r

Type: Void

[hash i for i in 1..5]

(1)

Type: List(Integer)

[morton(0,0,hash i,1) for i in 1..5]

Compiling function bits with type (NonNegativeInteger,
      NonNegativeInteger,NonNegativeInteger) -> SingleInteger

Compiling function bits with type (Integer,PositiveInteger,
      NonNegativeInteger) -> SingleInteger

Compiling function morton with type (NonNegativeInteger,
      NonNegativeInteger,Integer,PositiveInteger) -> SingleInteger

(2)

Type: List(SingleInteger)

listHash([1])

Compiling function bits with type (SingleInteger,NonNegativeInteger,
      NonNegativeInteger) -> SingleInteger

Compiling function morton with type (SingleInteger,
      NonNegativeInteger,Integer,PositiveInteger) -> SingleInteger

Compiling function listHash with type List(PositiveInteger) -> 
      SingleInteger

(3)

Type: SingleInteger

matrix [[listHash([i,j]) for j in 1..5] for i in 1..5]

(4)

Type: Matrix(SingleInteger)

matrix [[listHash([1,i,j]) for j in 1..5] for i in 1..5]

(5)

Type: Matrix(SingleInteger)

matrix [[listHash([2,i,j]) for j in 1..5] for i in 1..5]

(6)

Type: Matrix(SingleInteger)

Interleave bits by Binary Magic Numbers

This is a fast bit manipulation for combining two hash codes that does not use MOD of a large prime number. Based on the an algorithm by By Sean Eron Anderson.

Ref: http://graphics.stanford.edu/~seander/bithacks.html#InterleaveBMN

)abbrev package MORTON Morton
Morton() : with
    morton2: (SingleInteger,SingleInteger) -> SingleInteger
  == add

    -- Shift lower 16 bits of x to even positions of 32 bit word
    spread(x:SingleInteger):SingleInteger ==
      x := LOGAND(x,65535)$Lisp -- 16rFFFF = 2^16-1
      x := LOGAND(LOGIOR(x,ASH(x,8)$Lisp)$Lisp,16711935)$Lisp   -- 16r00FF00FF
      x := LOGAND(LOGIOR(x,ASH(x,4)$Lisp)$Lisp,252645135)$Lisp  -- 16r0F0F0F0F
      x := LOGAND(LOGIOR(x,ASH(x,2)$Lisp)$Lisp,858993459)$Lisp  -- 16r33333333
      x := LOGAND(LOGIOR(x,ASH(x,1)$Lisp)$Lisp,1431655765)$Lisp -- 16r55555555

    -- Interleave bits of x and y so the bits of x are in the odd positions
    -- and the bits of y are in the even positions of a 29 bit SingleInteger
    morton2(x:SingleInteger, y:SingleInteger):SingleInteger ==
      LOGAND(LOGIOR(spread y,ASH(spread x,1)$Lisp)$Lisp,536870911)$Lisp
      -- 16r1FFFFFFF = 2^29 -1

   Compiling FriCAS source code from file 
      /var/zope2/var/LatexWiki/3849729568657923935-25px003.spad using 
      old system compiler.
   MORTON abbreviates package Morton 
------------------------------------------------------------------------
   initializing NRLIB MORTON for Morton 
   compiling into NRLIB MORTON 
   compiling local spread : SingleInteger -> SingleInteger
Time: 0.03 SEC.

   compiling exported morton2 : (SingleInteger,SingleInteger) -> SingleInteger
Time: 0 SEC.

(time taken in buildFunctor:  0)

;;;     ***       |Morton| REDEFINED

;;;     ***       |Morton| REDEFINED
Time: 0 SEC.

   Cumulative Statistics for Constructor Morton
      Time: 0.03 seconds

   finalizing NRLIB MORTON 
   Processing Morton for Browser database:
--->-->Morton((morton2 ((SingleInteger) (SingleInteger) (SingleInteger)))): Not documented!!!!
--->-->Morton(constructor): Not documented!!!!
--->-->Morton(): Missing Description
; compiling file "/var/zope2/var/LatexWiki/MORTON.NRLIB/MORTON.lsp" (written 25 FEB 2010 11:18:47 PM):
; compiling (/VERSIONCHECK 2)
; compiling (DEFUN |MORTON;spread| ...)
; compiling (DEFUN |MORTON;morton2;3Si;2| ...)
; compiling (DEFUN |Morton| ...)
; compiling (DEFUN |Morton;| ...)
; compiling (MAKEPROP (QUOTE |Morton|) ...)
; compiling (MAKEPROP (QUOTE |Morton|) ...)

; /var/zope2/var/LatexWiki/MORTON.NRLIB/MORTON.fasl written
; compilation finished in 0:00:00.054
------------------------------------------------------------------------
   Morton is now explicitly exposed in frame initial 
   Morton will be automatically loaded when needed from 
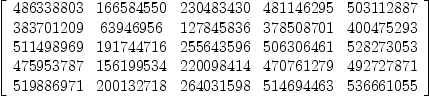
      /var/zope2/var/LatexWiki/MORTON.NRLIB/MORTON

matrix [[morton2(hash i,hash j) for j in 1..5] for i in 1..5]

(7)

Type: Matrix(SingleInteger)