fricas )show QuadraticForm fricas parse(s:String):InputForm == ncParseFromString(s)$Lisp pretend InputForm Type: Void
fricas parse("Integer")
fricas Compiling function parse with type String -> InputForm
Type: InputForm
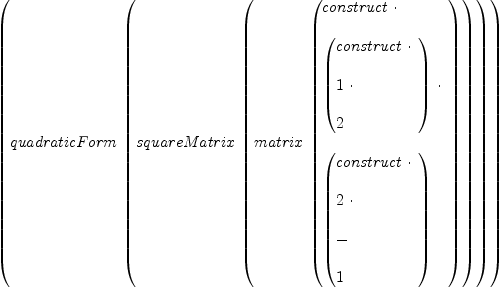
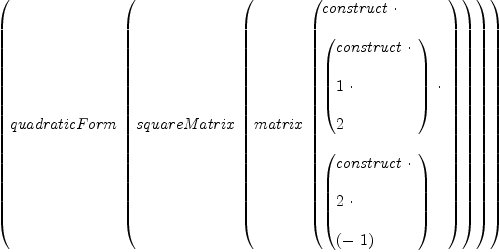
Test fricas qf := quadraticForm matrix [[1,
Type: QuadraticForm(2,
fricas qf::InputForm
Type: InputForm
fricas unparse %
Type: String
fricas parse %
Type: InputForm
fricas interpret(%)$INFORM1(QuadraticForm(2,
Type: QuadraticForm(2,
|
|
|
|
last edited 7 years ago by test1 |