Introduction
This file contains an implementation of rational interpolation, where the data
points are element of any integral domain.
Questions and Outlook
- Maybe this file should be joined with pinterp.spad, where polynomial
Lagrange interpolation is implemented. This version parallels the structure
of pinterp.spad closely. This also answers comments and questions from
wyscc. He remarked
- Abbreviations for a constructor should be limited to 7 letters (not 8).
The system occasionally adds the 8th character to a package for internal
use.
- Function names begin with a lower case, so RationalInterpolation should
be rationalInterpolation, or better, rationalInterpolate.
- Regarding the types I used for the values, wyscc remarked
- If we are doing a rational interpolation, presumably the values are
rational, so it does not make sense to require the
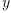 -coordinates of
inputs be integral. On the other hand, as in the above example, if one
uses
-coordinates of
inputs be integral. On the other hand, as in the above example, if one
uses FRAC INT, problems can arise when this package is combined with
other packages that constructs the quotient field of the parameter domain
F because Axiom does not like constructing FRAC FRAC INT.
Note however, that the package would rather construct the type FRAC SUP
FRAC INT, so this problem should not occur. Moreover, there are situations
- for example in the package [mantepse.spad2]?, where we want to interpolate values
from an IntegralDomain?. Of course we could first convert them to the
quotient field, however, the current approach seems more natural to me.
- Finally, wyscc asked:
If
p(xx) = interpolate(lx, ly, m, k), what is the purpose of
elt(px, qx) = p(qx), the composition of p(xx) and
qx, especially when qx is from FRAC UP(xx,
F) instead of from just F? and why is this function
(the composition) also called interpolate? I do not really know - apart from a very superficial level: Clearly, the
second function was intended to let the user easily plug in values into the
interpolated function. I don't find this sensible and I would be happy to
change it. Indeed, this would also get rid of the first parameter to
RINTERP, which is quite a nuisance.
I think we should agree on a general interface for interpolation
algorithms, and mark PINTERP as obsolete. By the way, it seems that
RINTERP is faster, too.
- There are probably better ways to implement rational interpolation. Maybe
http://www.cs.ucsb.edu/~omer/personal/abstracts/rational.html
contains something useful. In particular, in my package [mantepse.spad2]?, in
guessRat
and guessExpRat I generate interpolating polynomials for all possible degrees
of numerator and denominator. The above article contains an algorithm that does
this in time 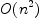 , which would be quite nice. Currently, I need
, which would be quite nice. Currently, I need 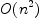 operations for each degree!
operations for each degree!
- For polynomial interpolation, there seems to be an algorithm that needs
only
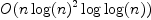 operations. It can be found in van zur Gathen's book
"Modern computer algebra", chapter 10.
operations. It can be found in van zur Gathen's book
"Modern computer algebra", chapter 10.
- For those who speak german,
http://www.num.math.uni-goettingen.de/schaback/teaching/numath.ps
contains quite a bit of information.
- This implementation of rational interpolation neither takes care of
unattainable points, nor does it check whether the values of the
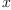 -coordinates are all distinct.
-coordinates are all distinct.
- Comments welcome!
spad
)abbrev package RINTERPA RationalInterpolationAlgorithms
++ Description:
++ This package exports rational interpolation algorithms
RationalInterpolationAlgorithms(F, P): Cat == Body where
F: IntegralDomain
P: UnivariatePolynomialCategory(F)
Cat == with
RationalInterpolation: (List F, List F, NonNegativeInteger,
NonNegativeInteger)
-> Fraction P
+++ We assume that the elements of the first list are all distinct.
+++ If they are not, division by zero might occur.
Body == add
RationalInterpolation(xlist, ylist, m, k) ==
#xlist ^= #ylist =>
error "Different number of points and values."
#xlist ^= m+k+1 =>
error "wrong number of points"
tempvec: List F := [1 for i in 1..(m+k+1)]
collist: List List F := cons(tempvec,
[(tempvec := [tempvec.i * xlist.i _
for i in 1..(m+k+1)]) _
for j in 1..max(m, k)])
collist := append([collist.j for j in 1..(m+1)], _
[[- collist.j.i * ylist.i for i in 1..(m+k+1)] _
for j in 1..(k+1)])
resspace: List Vector F := nullSpace((transpose matrix collist) _
::Matrix F)
reslist: List List P := _
[[monomial((resspace.1).(i+1), i) for i in 0..m], _
[monomial((resspace.1).(i+m+2), i) for i in 0..k]]
reduce((_+), reslist.1)/reduce((_+), reslist.2)
spad
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/959208282017174297-25px001.spad
using old system compiler.
RINTERPA abbreviates package RationalInterpolationAlgorithms
******** Spad syntax error detected ********
The prior line was:
15> RationalInterpolation(xlist, ylist, m, k) ==
The current line is:
16> #xlist ^= #ylist =>
The number of valid tokens is 2.
The prior token was #S(TOKEN
:SYMBOL ^
:TYPE KEYWORD
:NONBLANK NIL
:LINE_NUM 16
:CHAR_NUM 19)
The current token is #S(TOKEN
:SYMBOL =
:TYPE KEYWORD
:NONBLANK NIL
:LINE_NUM 16
:CHAR_NUM 20)
The next token is #S(TOKEN
:SYMBOL |#|
:TYPE KEYWORD
:NONBLANK NIL
:LINE_NUM 16
:CHAR_NUM 22)spad
)abbrev package RINTERP RationalInterpolation
++ Description:
++ This package exports interpolation algorithms
RationalInterpolation(xx, F): Cat == Body where
xx: Symbol
F: IntegralDomain
UP ==> UnivariatePolynomial
SUP ==> SparseUnivariatePolynomial
Cat == with
interpolate: (Fraction UP(xx, F), List F, List F, _
NonNegativeInteger, NonNegativeInteger) _
-> Fraction UP(xx, F)
interpolate: (List F, List F, NonNegativeInteger, NonNegativeInteger) _
-> Fraction SUP F
Body == add
RIA ==> RationalInterpolationAlgorithms
interpolate(qx, lx, ly, m, k) ==
px := RationalInterpolation(lx, ly, m, k)$RIA(F, UP(xx, F))
elt(px, qx)
interpolate(lx, ly, m, k) ==
RationalInterpolation(lx, ly, m, k)$RIA(F, SUP F)
spad
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/6898989268314666018-25px002.spad
using old system compiler.
RINTERP abbreviates package RationalInterpolation
------------------------------------------------------------------------
initializing NRLIB RINTERP for RationalInterpolation
compiling into NRLIB RINTERP
processing macro definition RIA ==> RationalInterpolationAlgorithms
compiling exported interpolate : (Fraction UnivariatePolynomial(xx,F),List F,List F,NonNegativeInteger,NonNegativeInteger) -> Fraction UnivariatePolynomial(xx,F)
****** comp fails at level 3 with expression: ******
error in function interpolate
(SEQ
(|:=| |px| | << |
((|Sel| (|RationalInterpolationAlgorithms| F (|UnivariatePolynomial| |xx| F))
|RationalInterpolation|)
|lx| |ly| |m| |k|)
| >> |)
(|exit| 1 (|elt| |px| |qx|)))
****** level 3 ******
$x:= ((Sel (RationalInterpolationAlgorithms F (UnivariatePolynomial xx F)) RationalInterpolation) lx ly m k)
$m:= $EmptyMode
$f:=
((((|k| # #) (|m| # #) (|ly| # #) (|lx| # #) ...)))
>> Apparent user error:
no modemap for RationalInterpolation with 4 argumentsFirst we check whether we have the right number of points and values. Clearly
the number of points and the number of values must be identical. Note that we
want to determine the numerator and denominator polynomials only up to a
factor. Thus, we want to determine 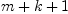 coefficients, where
coefficients, where 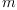 is the degree
of the polynomial in the numerator and
is the degree
of the polynomial in the numerator and 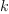 is the degree of the polynomial in
the denominator.
is the degree of the polynomial in
the denominator.
In fact, we could also leave - for example - 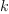 unspecified and determine it
as
unspecified and determine it
as 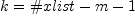 : I don't know whether this would be better.
: I don't know whether this would be better.
The next step is to set up the matrix. Suppose that our numerator polynomial is
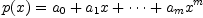 and that our denominator polynomial is
and that our denominator polynomial is
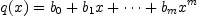 . Then we have the following equations, writing
. Then we have the following equations, writing 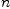 for
for 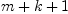 :
:
This can be written as
We generate this matrix columnwise, then we can solve the system using nullSpace.
Note that it may happen that the system has several solutions. In this case,
some of the data points may not be interpolated correctly. However, the
solution is often still useful, thus we do not signal an error.
Since all the solutions of nullSpace will be equivalent, we can always
simply take the first one. Finally, we return the rational function.
Examples
To conclude we present some examples. To begin with, the following interpolation
illustrates the concept of unattainable points:
fricas
interpolate([q,q^2,q^3],[0,x^1,x^2],0,2)$RINTERP(qn, FRAC POLY INT)
Type: Fraction(Polynomial(Fraction(Polynomial(Integer))))
fricas
f(x) == (x^3+5*x-3)/(x^2-3)
Type: Void
fricas
xlist := [1/2, 4, 1/6, 8, 1/10, 12]
Type: List(Fraction(Integer))
fricas
ylist := [f(x) for x in xlist]
fricas
Compiling function f with type Fraction(Integer) -> Fraction(Integer
)Type: List(Fraction(Integer))
fricas
interpolate(xlist, ylist, 3, 2)$RINTERP('x, FRAC INT)
Type: Fraction(Polynomial(Fraction(Integer)))
fricas
interpolate(1/6::FRAC UP(x,FRAC INT), xlist, ylist, 3, 2)$RINTERP('x,FRAC INT)
The function interpolate is not implemented in RationalInterpolation
(x,Fraction(Integer)) .
A harder example:
fricas
dom := DMP([z],INT);
Type: Type
fricas
g: FRAC dom -> FRAC dom;
Type: Void
fricas
g(x) == (x^3*z+5*z^2*x -3*z^3)/(z*x^2 - 3)
Type: Void
fricas
xxlist: List FRAC dom := [1/(2*z), 4*z, 1/(6*z), 8*z, 1/(10*z), 12*z]
Type: List(Fraction(DistributedMultivariatePolynomial
?([z],
Integer)))
fricas
yylist := [g(x) for x in xxlist]
fricas
Compiling function g with type Fraction(
DistributedMultivariatePolynomial([z],Integer)) -> Fraction(
DistributedMultivariatePolynomial([z],Integer))Type: List(Fraction(DistributedMultivariatePolynomial
?([z],
Integer)))
fricas
interpolate(xxlist, yylist, 3, 2)$RINTERP('x, FRAC dom)
Type: Fraction(Polynomial(Fraction(DistributedMultivariatePolynomial
?([z],
Integer))))
fricas
interpolate(4*z::FRAC UP(x,dom), xxlist, yylist, 3, 2)$RINTERP('x, FRAC dom)
The function interpolate is not implemented in RationalInterpolation
(x,Fraction(DistributedMultivariatePolynomial([z],Integer))) .
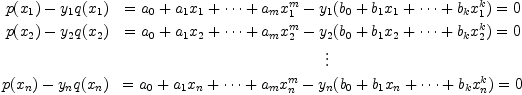
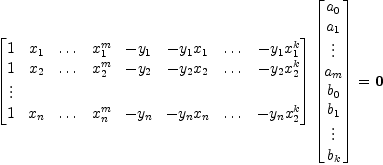
![\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{{24}\ {{z}^{5}}}-{{20}\ {{z}^{3}}}- 1}\over{{{24}\ {{z}^{2}}}-{2 \ z}}}, \:{{{{64}\ {{z}^{4}}}+{{17}\ {{z}^{3}}}}\over{{{1
6}\ {{z}^{3}}}- 3}}, \:{{{{648}\ {{z}^{5}}}-{{180}\ {{z}^{3}}}- 1}\over{{{648}\ {{z}^{2}}}-{6 \ z}}}, \: \right.
\
\
\displaystyle
\left.{{{{512}\ {{z}^{4}}}+{{37}\ {{z}^{3}}}}\over{{{64}\ {{z}^{3}}}- 3}}, \:{{{{3000}\ {{z}^{5}}}-{{500}\ {{z}^{3}}}- 1}\over{{{3
000}\ {{z}^{2}}}-{{10}\ z}}}, \:{{{{576}\ {{z}^{4}}}+{{19}\ {{z}^{3}}}}\over{{{48}\ {{z}^{3}}}- 1}}\right]
\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{{24}\ {{z}^{5}}}-{{20}\ {{z}^{3}}}- 1}\over{{{24}\ {{z}^{2}}}-{2 \ z}}}, \:{{{{64}\ {{z}^{4}}}+{{17}\ {{z}^{3}}}}\over{{{1
6}\ {{z}^{3}}}- 3}}, \:{{{{648}\ {{z}^{5}}}-{{180}\ {{z}^{3}}}- 1}\over{{{648}\ {{z}^{2}}}-{6 \ z}}}, \: \right.
\
\
\displaystyle
\left.{{{{512}\ {{z}^{4}}}+{{37}\ {{z}^{3}}}}\over{{{64}\ {{z}^{3}}}- 3}}, \:{{{{3000}\ {{z}^{5}}}-{{500}\ {{z}^{3}}}- 1}\over{{{3
000}\ {{z}^{2}}}-{{10}\ z}}}, \:{{{{576}\ {{z}^{4}}}+{{19}\ {{z}^{3}}}}\over{{{48}\ {{z}^{3}}}- 1}}\right]](images/6690073116057656186-16.0px.png)