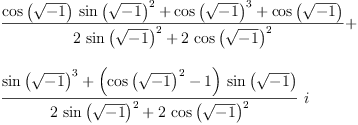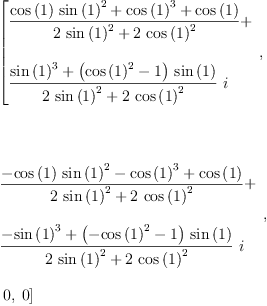Biquaternion Calculus Domain
D. Cyganski and Bill Page - July 2007
This version is implemented as a new domain in Aldor .
fricas
(1) -> <aldor>
#pile
#include "fricas"
import from NonNegativeInteger
BiQuaternion(R:Join(OrderedSet,CommutativeRing)): Exports == Implementation where
C==>Complex Expression R
Exports ==> QuaternionCategory(C) with
qlist: List C -> %
-- takes a complex list (parameter l) into a quaternion
listq: % -> List C
-- takes a quaternion into a list
matrixq: % -> SquareMatrix(2,C)
-- takes a quaternion into a matrix
sig0:%
sig1:%
sig2:%
sig3:%
siglist: % -> List C
-- Pauli basis representation of the biquaternion
if Complex(Expression(R)) has PartialDifferentialRing(Symbol) then
D: (%,Symbol,Symbol,Symbol) -> %
-- quaternion derivative
rot: (C,%) -> %
-- biquaternion rotation
/: (%,%) -> %
/: (C,%) -> %
/: (%,C) -> %
abs: % -> C
exp: % -> %
coerce: Complex R -> %
Implementation ==> Quaternion C add
import from C
coerce(z:Complex R):% ==
import from Expression(R),ComplexFunctions2(R,Expression R)
map(coerce,z)::%
-- Define a function that takes a complex list (parameter l) into a quaternion
qlist(l:List C):%==
import from Integer
quatern(l 1,l 2,l 3,l 4)
-- Define a function that takes a quaternion into a list
listq(x:%):List C == [real x, imagI x, imagJ x, imagK x]
-- Define a function that takes a biquat into a matrix
matrixq(x:%):SquareMatrix(2,C) ==
import from List List C
matrix [[real x + imaginary()*imagI(x), imagJ x + imaginary()*imagK(x)],
[-imagJ(x) + imaginary()*imagK(x), real x - imaginary()*imagI(x)]]
-- Define a function that produces the Pauli basis representation of the biquaternion
siglist(x:%):List C == [real x, -imaginary()*imagK(x),-imaginary()*imagJ(x),imaginary()*imagI(x)]
sig0:% == quatern(1,0,0,0)
sig1:% == imaginary() * quatern(0,0,0,1)
sig2:% == imaginary() * quatern(0,0,1,0)
sig3:% == -imaginary() * quatern(0,1,0,0)
-- Define the quaternion derivative (Morgan, 2001, Eq. 2)
if Complex(Expression(R)) has PartialDifferentialRing(Symbol) then
D(q:%,x:Symbol,y:Symbol,z:Symbol):% == sig1*D(q,x)+sig2*D(q,y)+sig3*D(q,z)
-- Define a biquaternion rotation operator that takes a biquat through a rotation
-- of theta radians about the axis defined by the unit q biquat (Morgan 2001, Eq 3).
rot(theta:C,q:%):% ==
import from Integer, SparseMultivariatePolynomial(Integer, Kernel(C))
cos(theta/2::C)::% - imaginary()*q*sin(theta/2::C)
((x:%)/(y:%)):% == x*inv(y)
((x:C)/(y:%)):% == (x::%)*inv(y)
((x:%)/(y:C)):% == x*inv(y::%)
abs(q:%):C ==
sqrt(retract(q*conjugate(q)))
exp(q:%):% ==
import from Integer, SparseMultivariatePolynomial(Integer, Kernel(C))
q-conjugate(q)=0 => exp(retract(q+conjugate(q))/2::C)*sig0
exp(retract(q+conjugate(q))/2::C) * (sig0*cos(abs(q)) + (q-conjugate(q))/abs(q-conjugate(q)) * sin(abs(q)))</aldor>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/8265291018112466544-25px001.as
using Aldor compiler and options
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
Use the system command )set compiler args to change these
options.fricas
Compiling Lisp source code from file
./8265291018112466544-25px001.lsp
Issuing )library command for 8265291018112466544-25px001fricas
Reading /var/aw/var/LatexWiki/8265291018112466544-25px001.asy
BiQuaternion is now explicitly exposed in frame initial
BiQuaternion will be automatically loaded when needed from
/var/aw/var/LatexWiki/8265291018112466544-25px001fricas
)show BiQuaternion
BiQuaternion(R: Join(OrderedSet,CommutativeRing)) is a domain constructor
Abbreviation for BiQuaternion is BIQUAT
This constructor is exposed in this frame.
------------------------------- Operations --------------------------------
0 : () -> % 1 : () -> %
sample : () -> % sig0 : () -> %
sig1 : () -> % sig2 : () -> %
sig3 : () -> %
?*? : (%, Integer) -> % if Complex(Expression(R)) has LINEXP(INT)
?*? : (%, Fraction(Integer)) -> % if Complex(Expression(R)) has FIELD
?*? : (Fraction(Integer), %) -> % if Complex(Expression(R)) has FIELD
?<=? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
?>? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
?>=? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
D : % -> % if Complex(Expression(R)) has DIFRING
D : (%, NonNegativeInteger) -> % if Complex(Expression(R)) has DIFRING
D : (%, Symbol) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
D : (%, List(Symbol)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
D : (%, Symbol, NonNegativeInteger) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
D : (%, List(Symbol), List(NonNegativeInteger)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
D : (%, Symbol, Symbol, Symbol) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
?^? : (%, Integer) -> % if Complex(Expression(R)) has FIELD
associates? : (%, %) -> Boolean if Complex(Expression(R)) has ENTIRER
associates? : (%, %) -> Boolean if Complex(Expression(R)) has FIELD
charthRoot : % -> Union(value1: %,failed: Enumeration(failed)) if Complex(Expression(R)) has CHARNZ
differentiate : (%, NonNegativeInteger) -> % if Complex(Expression(R)) has DIFRING
differentiate : (%, List(Symbol)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
differentiate : (%, Symbol, NonNegativeInteger) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
differentiate : (%, List(Symbol), List(NonNegativeInteger)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
eval : (%, Complex(Expression(R)), Complex(Expression(R))) -> % if Complex(Expression(R)) has EVALAB(COMPLEX(EXPR(R)))
eval : (%, List(Complex(Expression(R))), List(Complex(Expression(R)))) -> % if Complex(Expression(R)) has EVALAB(COMPLEX(EXPR(R)))
eval : (%, Equation(Complex(Expression(R)))) -> % if Complex(Expression(R)) has EVALAB(COMPLEX(EXPR(R)))
eval : (%, Symbol, Complex(Expression(R))) -> % if Complex(Expression(R)) has IEVALAB(SYMBOL,COMPLEX(EXPR(R)))
exquo : (%, %) -> Union(value1: %,failed: Enumeration(failed)) if Complex(Expression(R)) has ENTIRER
exquo : (%, %) -> Union(value1: %,failed: Enumeration(failed)) if Complex(Expression(R)) has FIELD
max : (%, %) -> % if Complex(Expression(R)) has ORDSET
min : (%, %) -> % if Complex(Expression(R)) has ORDSET
smaller? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
unit? : % -> Boolean if Complex(Expression(R)) has ENTIRER
unit? : % -> Boolean if Complex(Expression(R)) has FIELD
unitCanonical : % -> % if Complex(Expression(R)) has ENTIRER
unitCanonical : % -> % if Complex(Expression(R)) has FIELD
unitNormal : % -> Record(unit: %,canonical: %,associate: %) if Complex(Expression(R)) has ENTIRER
unitNormal : % -> Record(unit: %,canonical: %,associate: %) if Complex(Expression(R)) has FIELD
fricas
Q := BiQuaternion Integer
Type: Type
fricas
q:Q := quatern(q0,q1,q2,q3)
Type: BiQuaternion
?(Integer)
For testing the derivative we define this set of operators
fricas
Ft:=operator 'Ft; Fx:=operator 'Fx; Fy:=operator 'Fy; Fz:=operator 'Fz;
Now form a general quaternion which is a function of x,y,z
fricas
F:Q:=Ft(x,y,z)*sig0()+Fx(x,y,z)*sig1()+Fy(x,y,z)*sig2()+Fz(x,y,z)*sig3()
Type: BiQuaternion
?(Integer)
In the Pauli basis the derivative of this biquat should produce (Morgan 2001, eq 1):
D(Ft+F.sigma)=div(F)+(grad(Ft)+%i*curl(F)).sigma
which it does
fricas
siglist(D(F,x,y,z))
Type: List(Complex(Expression(Integer)))
Test
(comment out this test later)
fricas
%i::Q
Type: BiQuaternion
?(Integer)
fricas
abs(%i::Q)
Type: Complex(Expression(Integer))
fricas
abs(q)
Type: Complex(Expression(Integer))
fricas
cos(abs(%i::Q))
Type: Complex(Expression(Integer))
If I've defined these correctly, then the rotation about the x axis defined by qx below by 2 radians
should give the same answer as exponentiation to -%i*qx (not a very complete test)
fricas
qx:Q:=sig1()
Type: BiQuaternion
?(Integer)
fricas
siglist(rot(2,qx))
Type: List(Complex(Expression(Integer)))
fricas
siglist(exp(-%i::Q*qx))
Type: List(Complex(Expression(Integer)))
which it does
fricas
(%%(-1)=%%(-2))@Boolean
Type: Boolean
I would love to express a proof of equality such as:
rot(theta,q) = exp((-theta/2)*%i*q)
for arbitrary real 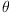 and biquaternion q as I would in Maple.
and biquaternion q as I would in Maple.
fricas
theta:Complex Expression Integer := _\theta
Type: Complex(Expression(Integer))
fricas
map(simplify, siglist( rot(theta,q) - exp((-%i*theta/2) * q)))::List Expression Complex Integer
Type: List(Expression(Complex(Integer)))
fricas
map(simplify,siglist(rot(2,qx)))::List Expression Complex Integer
Type: List(Expression(Complex(Integer)))
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{{Fz_{, 3}}\left({x , \: y , \: z}\right)}+{{Fy_{, 2}}\left({x , \: y , \: z}\right)}+{{Fx_{, 1}}\left({x , \: y , \: z}\right)}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 1}}\left({x , \: y , \: z}\right)}+{{\left({{Fz_{, 2}}\left({x , \: y , \: z}\right)}-{{Fy_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 2}}\left({x , \: y , \: z}\right)}+{{\left(-{{Fz_{, 1}}\left({x , \: y , \: z}\right)}+{{Fx_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 3}}\left({x , \: y , \: z}\right)}+{{\left({{Fy_{, 1}}\left({x , \: y , \: z}\right)}-{{Fx_{, 2}}\left({x , \: y , \: z}\right)}\right)}\ i}}\right]
\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{{Fz_{, 3}}\left({x , \: y , \: z}\right)}+{{Fy_{, 2}}\left({x , \: y , \: z}\right)}+{{Fx_{, 1}}\left({x , \: y , \: z}\right)}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 1}}\left({x , \: y , \: z}\right)}+{{\left({{Fz_{, 2}}\left({x , \: y , \: z}\right)}-{{Fy_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 2}}\left({x , \: y , \: z}\right)}+{{\left(-{{Fz_{, 1}}\left({x , \: y , \: z}\right)}+{{Fx_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 3}}\left({x , \: y , \: z}\right)}+{{\left({{Fy_{, 1}}\left({x , \: y , \: z}\right)}-{{Fx_{, 2}}\left({x , \: y , \: z}\right)}\right)}\ i}}\right]](images/6063581373477545935-16.0px.png)