Special relativity without Lorentz transformations.Here are some sample computations based on papers by Z. Oziewicz
and the book by T. Matolcsi See also the slides: SandBoxRelativeVelocity (presented at IARD 2006). Mathematical PreliminariesA vector is represented as a nx1 matrix (column vector) fricas (1) -> vect(x:List Expression Integer):Matrix Expression Integer == matrix map(y+->[y], Type: Void
fricas vect [a1, fricas Compiling function vect with type List(Expression(Integer)) ->
Matrix(Expression(Integer))
Type: Matrix(Expression(Integer))
Then a row vector is fricas transpose(vect [a1,
Type: Matrix(Expression(Integer))
Inner product is fricas transpose(vect [a1,
Type: Matrix(Expression(Integer))
and tensor product is fricas vect [a1,
Type: Matrix(Expression(Integer))
Applying the Lorentz form produces a row vector fricas g(x)==transpose(x)*diagonalMatrix [-1, Type: Void
or a scalar fricas g(x, Type: Void
For difficult verifications it is sometimes convenient to replace symbols by random numerical values. fricas possible(x)==subst(x, Type: Void
fricas Is?(eq:Equation EXPR INT):Boolean == (lhs(eq)-rhs(eq)=0)::Boolean Type: Void
fricas Is2?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _ ( (lhs(eq)-rhs(eq)) :: Matrix Expression AlgebraicNumber = _ zero(nrows(lhs(eq)), Type: Void
The AlgebraicNumber? domain can test for numerical equality of complicated
expressions involving fricas IsPossible?(eq:Equation EXPR INT):Boolean == _ (possible(lhs(eq)-rhs(eq)) :: Expression AlgebraicNumber=0)::Boolean Type: Void
fricas IsPossible2?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _ ( map(possible, Type: Void
Massive ObjectsAn object (also referred to as an obserser) is represented by a time-like 4-vector fricas P:=vect [sqrt(p1^2+p2^2+p3^2+1), Type: Matrix(Expression(Integer))
fricas g(P, fricas Compiling function g with type (Matrix(Expression(Integer)),
Type: Expression(Integer)
fricas Q:=vect [sqrt(q1^2+q2^2+q3^2+1), Type: Matrix(Expression(Integer))
fricas g(Q,
Type: Expression(Integer)
Associated with each such vector is the orthogonal 3-d Euclidean subspace
Relative VelocityAn object Q has a unique relative velocity w(P,Q) with respect to object P given by fricas w(P, Type: Void
Lorentz factor fricas gamma(v)==1/sqrt(1-g(v, Type: Void
Binary Boost fricas b(P, Type: Void
Observer P measures velocity u. u is space-like and in fricas u:=w(P, fricas Compiling function w with type (Matrix(Expression(Integer)), Type: Matrix(Expression(Integer))
fricas g(P,
Type: Expression(Integer)
fricas possible(g(u, fricas Compiling function possible with type Expression(Integer) ->
Expression(Integer)
Type: Expression(Float)
fricas IsPossible?(gamma(u)=-g(P, fricas Compiling function gamma with type Matrix(Expression(Integer)) ->
Expression(Integer)fricas Compiling function IsPossible? with type Equation(Expression(Integer
)) -> Boolean
Type: Boolean
u is velocity of object Q fricas IsPossible?(g(Q,
Type: Boolean
Observer Q is u-boost of P fricas IsPossible2?(Q=b(P, fricas Compiling function b with type (Matrix(Expression(Integer)), fricas Compiling function IsPossible2? with type Equation(Matrix(Expression
(Integer))) -> Boolean
Type: Boolean
Inverse velocity is measured by Q fricas u' := w(Q, Type: Matrix(Expression(Integer))
fricas g(Q,
Type: Expression(Integer)
Inverse velocity is not reciprocal fricas IsPossible2?(-u=u')
Type: Boolean
Object P is u'-boost of Q fricas IsPossible2?(P=b(Q,
Type: Boolean
Objects P and Q are completely determined by velocities u and u' fricas IsPossible2?(P = -1/g(u,
Type: Boolean
fricas IsPossible2?(Q = -1/g(u,
Type: Boolean
The magnitude of the inverse velocity is the same as the velocity fricas IsPossible?(g(u,
Type: Boolean
Collinear VelocitiesSuppose the velocity v of some object L is collinear with reciprocal velocity u': fricas v := alpha*u'; Type: Matrix(Expression(Integer))
fricas L := b(Q, Type: Matrix(Expression(Integer))
fricas Is2?(v=w(Q, fricas Compiling function Is2? with type Equation(Matrix(Expression(Integer
))) -> Boolean
Type: Boolean
Composition of collinear velocitiesFor velocity v collinear with reciprocal velocity u' we have Matolcsi (4.3.3) fricas Is2?(w(P,
Type: Boolean
General composition of relative velocities (Oziewicz) fricas compose(v, Type: Void
fricas Is2?(w(P, fricas Compiling function compose with type (Matrix(Expression(Integer)),
Type: Boolean
fricas IsPossible2?(w(P,
Type: Boolean
Associativity Unlike Einstein addition of velocities, composition (denoted
fricas R:=vect [sqrt(r1^2+r2^2+r3^2+1), Type: Matrix(Expression(Integer))
fricas g(R,
Type: Expression(Integer)
fricas S:=vect [sqrt(s1^2+s2^2+s3^2+1), Type: Matrix(Expression(Integer))
fricas g(S,
Type: Expression(Integer)
Unfortunately Axiom is not able to evaluate all of these in a reasonable amount of time (within the 1 minute wiki limit). fricas --IsPossible2?(w(P,
Type: Boolean
fricas --IsPossible2?(w(P,
Type: NonNegativeInteger?
|
|
|
|
last edited 10 years ago by Bill Page |
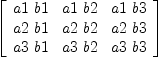
![.
\psfrag{alpha}[cc][cc]{$v \oplus u$}
\psfrag{beta}[cc][cc]{$w \oplus v$}
\psfrag{gamma}[cc][cc]{$(w\oplus v)+u=w\oplus (v\oplus u)$}
\digraph[scale=0.9]{CategoricalRelativity2}{rankdir=LR; P->Q [label="u"];
Q->R [label="v"]; R->S [label="w"]; P->R [label="alpha"]; Q->S [label="beta"];
P->S [label="gamma"]; }
.
\psfrag{alpha}[cc][cc]{$v \oplus u$}
\psfrag{beta}[cc][cc]{$w \oplus v$}
\psfrag{gamma}[cc][cc]{$(w\oplus v)+u=w\oplus (v\oplus u)$}
\digraph[scale=0.9]{CategoricalRelativity2}{rankdir=LR; P->Q [label="u"];
Q->R [label="v"]; R->S [label="w"]; P->R [label="alpha"]; Q->S [label="beta"];
P->S [label="gamma"]; }](images/4496217591658828580-16.0px.png)