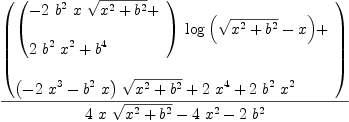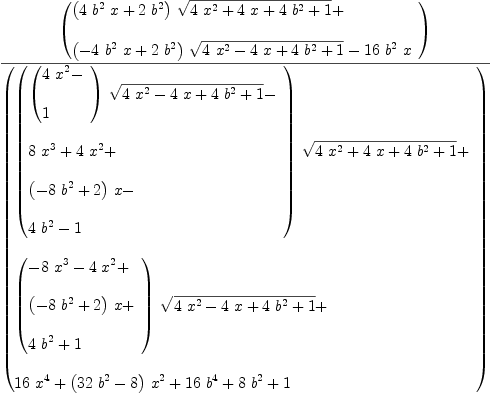DistributionsWe represent distributions as a complex function in the limit where the imaginary part goes to 0. Signum (sign), delta and doublet functions arise from the derivative of the absolute value function with respect to its real part. Ref.
Use definition of conjugate and derivative of abs(x) from SandBoxFunctionalSpecialFunction fricas )lib FSPECX Type: Void
Absolute value as a function of real or complex variables fricas abs(z:Expression Integer):Expression Integer == sqrt(z*conjugate(z)); abs(z) fricas Compiling function abs with type Expression(Integer) -> Expression(
Integer)
Type: Expression(Integer)
fricas abz(a:Expression Integer):Expression Integer == sqrt((a+%i*b)*(a-%i*b)); abz(x) fricas Compiling function abz with type Expression(Integer) -> Expression(
Integer)
Type: Expression(Integer)
Total Wirtinger derivatives of this complex function (CR-calculus) fricas abs':=wirtingerD(abs(z), fricas Compiling function wirtingerD with type (Expression(Integer), fricas Compiling function wirtingerD with type (Expression(Integer),
Type: Expression(Integer)
fricas abs'':=wirtingerD(abs',
Type: Expression(Integer)
fricas abs''':=wirtingerD(abs'',
Type: Expression(Integer)
Consider these as complex functions of fricas realSignum:Expression Integer:=eval(eval(abs',
Type: Expression(Integer)
fricas test(realSignum=D(abz(a),
Type: Boolean
fricas signum(x)==eval(realSignum, fricas Compiling function signum with type Variable(x) -> Expression(
Integer)
Type: Expression(Integer)
fricas -- realDirac:Expression Integer:=eval(eval(abs'',
Type: Expression(Integer)
fricas test(realDirac=D(abz(a),
Type: Boolean
fricas diracDelta(x)==eval(realDirac/2, fricas Compiling function diracDelta with type Variable(x) -> Expression(
Integer)
Type: Expression(Integer)
fricas -- realUnitDoublet:Expression Integer:=eval(eval(abs''',
Type: Expression(Integer)
fricas test(realUnitDoublet=D(abz(a),
Type: Boolean
fricas unitDoublet(x)==eval(-realUnitDoublet/2, fricas Compiling function unitDoublet with type Variable(x) -> Expression(
Integer)
Type: Expression(Integer)
We are interested in the behavior of these functions in the limit as
signum Properties fricas limit( signum(1) , fricas Compiling function signum with type PositiveInteger -> Expression(
Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( signum(-1) , fricas Compiling function signum with type Integer -> Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( signum(0) , fricas Compiling function signum with type NonNegativeInteger -> Expression
(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( signum(x)^2 ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas -- odd function test( signum(x)=-signum(-x)) fricas Compiling function signum with type Polynomial(Integer) ->
Expression(Integer)
Type: Boolean
diracDelta Properties fricas limit( diracDelta(1) , fricas Compiling function diracDelta with type PositiveInteger ->
Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( diracDelta(-1) , fricas Compiling function diracDelta with type Integer -> Expression(
Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( diracDelta(0) , fricas Compiling function diracDelta with type NonNegativeInteger ->
Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas -- even function test( diracDelta(x)=diracDelta(-x) ) fricas Compiling function diracDelta with type Polynomial(Integer) ->
Expression(Integer)
Type: Boolean
fricas limit( diracDelta(x)^2 ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas integrate(diracDelta(x),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas f(x)==c1*x+c2 Type: Void
fricas test(integrate(f(x)*diracDelta(x-t), fricas Compiling function f with type Variable(x) -> Polynomial(Integer) fricas Compiling function f with type Variable(t) -> Polynomial(Integer)
Type: Boolean
fricas limit(integrate(log(x)*diracDelta(x-t),
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas eval(%,
Type: Expression(Integer)
fricas integrate(diracDelta(2*x),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas -- limit( signum(x)*diracDelta(x) ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit(diracDelta(x^2),
Type: Union(OrderedCompletion?(Expression(Integer)),
The Unit Doublet function comes after diracDelta fricas test(unitDoublet(x)=3*diracDelta(x)*signum(x)/abz(x))
Type: Boolean
fricas limit( unitDoublet(1) , fricas Compiling function unitDoublet with type PositiveInteger ->
Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( unitDoublet(-1) , fricas Compiling function unitDoublet with type Integer -> Expression(
Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( unitDoublet(0) , fricas Compiling function unitDoublet with type NonNegativeInteger ->
Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas -- odd function test( unitDoublet(x)=-unitDoublet(-x) ) fricas Compiling function unitDoublet with type Polynomial(Integer) ->
Expression(Integer)
Type: Boolean
fricas limit( unitDoublet(x)^2 ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas integrate(unitDoublet(x),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas f(x)==c1*x^2+c2*x+c3 Type: Void
fricas test(integrate(f(x)*unitDoublet(x-t), fricas Compiling function f with type Variable(x) -> Polynomial(Integer)
Type: Boolean
fricas integrate(unitDoublet(2*x),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas -- limit( signum(x)*unitDoublet(x) ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( diracDelta(x)*unitDoublet(x) ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( unitDoublet(x^2) ,
Type: Union(OrderedCompletion?(Expression(Integer)),
Heaviside fricas realHeaviside:Expression Integer := integrate(diracDelta(a), fricas Compiling function diracDelta with type Variable(a) -> Expression(
Integer)
Type: Expression(Integer)
fricas heavisideStep(x)==eval(realHeaviside, Type: Void
fricas limit( heavisideStep(1), fricas Compiling function heavisideStep with type PositiveInteger ->
Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( heavisideStep(-1) , fricas Compiling function heavisideStep with type Integer -> Expression(
Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( heavisideStep(0) , fricas Compiling function heavisideStep with type NonNegativeInteger ->
Expression(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( heavisideStep(x), fricas Compiling function heavisideStep with type Variable(x) -> Expression
(Integer)
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( heavisideStep(x) ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas limit( heavisideStep(x) ,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas test(simplify( (1+signum(x))/2 - heavisideStep(x) ) = 0)
Type: Boolean
fricas test(limit( integrate(heavisideStep(t), fricas Compiling function heavisideStep with type Variable(t) -> Expression
(Integer)
Type: Boolean
fricas -- diracDelta? d1:=integrate(heavisideStep(t)*unitDoublet(t), fricas Compiling function unitDoublet with type Variable(t) -> Expression(
Integer)
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas simplify(d1-diracDelta(x))
Type: Expression(Integer)
Problems? fricas -- expected 1/abs(c) integrate(diracDelta(c*x),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas f(x)==c1*x^2+c2*x+c3 Type: Void
fricas integrate(f(x)*diracDelta(x-t), fricas Compiling function f with type Variable(x) -> Polynomial(Integer)
Type: Union(fail: failed,
fricas -- expected f(t) fricas Compiling function f with type Variable(t) -> Polynomial(Integer)
Type: Polynomial(Integer)
fricas -- expected 1 integrate(exp(x)*diracDelta(x),
Type: Union(fail: failed,
fricas -- expected 1 integrate(exp(x)*unitDoublet(x),
Type: Union(fail: failed,
fricas -- loops forever on %plusInfinity limit of indefinite integral --integrate(log(x)*unitDoublet(x-t),
Type: Union(Expression(Integer),
fricas integrate(abz(x),
Type: Union(Expression(Integer),
fricas limit(%,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas -- expected abs(x) integrate(abs',
Type: Union(Expression(Integer),
fricas integrate(signum(x),
Type: Union(Expression(Integer),
fricas limit(%,
Type: Union(OrderedCompletion?(Expression(Integer)),
fricas -- expected signum(x)/2 integrate(abs'',
Type: Union(Expression(Integer),
fricas integrate(diracDelta(x^2+y^2),
Type: Union(fail: failed,
Convolution fricas g(x)==abz(x)/2; g(y) fricas Compiling function g with type Variable(y) -> Expression(Integer)
Type: Expression(Integer)
fricas h(x)==heavisideStep(x+1/2)-heavisideStep(x-1/2); h(x) fricas Compiling function heavisideStep with type Polynomial(Fraction(
Integer)) -> Expression(Integer)fricas Compiling function h with type Variable(x) -> Expression(Integer)
Type: Expression(Integer)
fricas conv:=integrate(h(x-y)*g(y), fricas Compiling function h with type Polynomial(Integer) -> Expression(
Integer)
Type: Union(fail: failed,
Representing a distribution as a series of bump functions fricas )lib GDRAW Type: List(DoubleFloat?)
fricas Y:=[eval(unitDoublet(x), fricas Compiling function unitDoublet with type DoubleFloat -> Expression(
DoubleFloat)Type: List(DoubleFloat?)
fricas gnuDraw(X, Type: Void
![[terminal=pslatex,terminaloptions=color,scale=1.3]
load "SandBoxDiracDeltaX2.dat"
[terminal=pslatex,terminaloptions=color,scale=1.3]
load "SandBoxDiracDeltaX2.dat"](images/630124311021293120-16.0px.png)
|
|
|
|
last edited 9 years ago by Bill page |