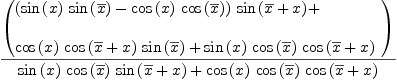MathAction SandBoxElementaryFunctionStructurePackage

Topics

FrontPage
- HistoricAxiom
  - AxiomDocumentation
    - Axiom Algebra
      - SandBoxElementaryFunctionStructurePackage <-- You are here.

fricas

)lib FSPECX

   FunctionalSpecialFunction is now explicitly exposed in frame initial

   FunctionalSpecialFunction will be automatically loaded when needed 
      from /var/aw/var/LatexWiki/FSPECX.NRLIB/FSPECX

spad

)abbrev package EFSTRUX ElementaryFunctionStructurePackage
++ Risch structure theorem
++ Author: Manuel Bronstein, Waldek Hebisch
++ Date Created: 1987
++ Date Last Updated: 9 October 2006
++ Description:
++   ElementaryFunctionStructurePackage provides functions to test the
++   algebraic independence of various elementary functions, using the
++   Risch structure theorem (real and complex versions).
++   It also provides transformations on elementary functions
++   which are not considered simplifications.
++ Keywords: elementary, function, structure.
ElementaryFunctionStructurePackage(R, F) : Exports == Implementation where
  R : Join(IntegralDomain, Comparable, RetractableTo Integer,
           LinearlyExplicitRingOver Integer)
  F : Join(AlgebraicallyClosedField, TranscendentalFunctionCategory,
           FunctionSpace R)

  B   ==> Boolean
  N   ==> NonNegativeInteger
  Z   ==> Integer
  Q   ==> Fraction Z
  SY  ==> Symbol
  K   ==> Kernel F
  UP  ==> SparseUnivariatePolynomial F
  SMP ==> SparseMultivariatePolynomial(R, K)
  REC ==> Record(func : F, kers : List K, vals : List F)
  U   ==> Union(vec : Vector Q, func : F, fail : Boolean)
  POWER ==> '%power
  NTHR  ==> 'nthRoot

  Exports ==> with
    normalize : F -> F
      ++ normalize(f) rewrites \spad{f} using the least possible number of
      ++ real algebraically independent kernels.
    normalize : (F, SY) -> F
      ++ normalize(f, x) rewrites \spad{f} using the least possible number of
      ++ real algebraically independent kernels involving \spad{x}.
    rischNormalize : (F, SY) -> REC
      ++ rischNormalize(f, x) returns \spad{[g, [k1, ..., kn], [h1, ..., hn]]}
      ++ such that \spad{g = normalize(f, x)} and each \spad{ki} was
      ++ rewritten as \spad{hi} during the normalization.
    rischNormalize : (F, List SY) -> REC
      ++ rischNormalize(f, lx) returns \spad{[g, [k1, ..., kn], [h1, ..., hn]]}
      ++ such that \spad{g = normalize(f, lx)} and each \spad{ki} was
      ++ rewritten as \spad{hi} during the normalization.
    realElementary : F -> F
      ++ realElementary(f) rewrites \spad{f} in terms of the 4 fundamental real
      ++ transcendental elementary functions: \spad{log, exp, tan, atan}.
    realLiouvillian : F -> F
      ++ realLiouvillian(f) rewrites \spad{f} elementary kernels of f in
      ++ terms 4 fundamental real elementary functions: \spad{log, exp, tan,
      ++ atan}.  Additionally, it rewrites Liouvillian functions as
      ++ indefinite integrals to support better normalization.
    realLiouvillian : (F, SY) -> F
      ++ realLiouvillian(f, x) rewrites \spad{f} elementary kernels of f in
      ++ terms 4 fundamental real elementary functions: \spad{log, exp, tan,
      ++ atan}.  Additionally, it rewrites Liouvillian functions of x as
      ++ indefinite integrals to support better normalization.
    realElementary : (F, SY) -> F
      ++ realElementary(f, x) rewrites the kernels of \spad{f} involving \spad{x}
      ++ in terms of the 4 fundamental real
      ++ transcendental elementary functions: \spad{log, exp, tan, atan}.
    validExponential : (List K, F, SY) -> Union(F, "failed")
      ++ validExponential([k1, ..., kn], f, x) returns \spad{g} if \spad{exp(f)=g}
      ++ and \spad{g} involves only \spad{k1...kn}, and "failed" otherwise.
    rootNormalize : (F, K) -> F
      ++ rootNormalize(f, k) returns \spad{f} rewriting either \spad{k} which
      ++ must be an nth-root in terms of radicals already in \spad{f}, or some
      ++ radicals in \spad{f} in terms of \spad{k}.
    rmap : (K -> F, F) -> F
      ++ rmap(f, e) rewrites e replacing each kernel k in e by f(k)
    tanQ : (Q, F) -> F
      ++ tanQ(q, a) is a local function with a conditional implementation.
    irootDep : K -> U
      ++ irootDep(k) is a local function with a conditional implementation.

  Implementation ==> add
    import from TangentExpansions F
    import from IntegrationTools(R, F)
    import from IntegerLinearDependence F
    import from AlgebraicManipulations(R, F)
    import from InnerCommonDenominator(Z, Q, Vector Z, Vector Q)
    P  ==> SparseMultivariatePolynomial(R, K)

    HTRIG := 'htrig
    TRIG := 'trig

    k2Elem             : (K, List SY) -> F
    realElem           : (F, List SY) -> F
    rootDep            : (List K, K)     -> U
    findQRelation      : (List SY, List F, F) -> U
    findRelation       : (List SY, List SY, List K, K) -> U
    factdeprel         : (List K, K)     -> U
    toR                : (List K, F) -> List K
    toY                : List K -> List F
    toZ                : List K -> List F
    toU                : List K -> List F
    toV                : List K -> List F
    ktoY               : K  -> F
    ktoZ               : K  -> F
    ktoU               : K  -> F
    ktoV               : K  -> F
    gdCoef?            : (Q, Vector Q) -> Boolean
    goodCoef           : (Vector Q, List K, SY) ->
                                 Union(Record(index:Z, ker:K), "failed")
    tanRN              : (Q, K) -> F
    localnorm          : F -> F
    rooteval           : (F, List K, K, Q) -> REC
    logeval            : (F, List K, K, Vector Q) -> REC
    expeval            : (F, List K, K, Vector Q) -> REC
    taneval            : (F, List K, K, Vector Q) -> REC
    ataneval           : (F, List K, K, Vector Q) -> REC
    depeval            : (F, List K, K, Vector Q) -> REC
    expnosimp          : (F, List K, K, Vector Q, List F, F) -> REC
    tannosimp          : (F, List K, K, Vector Q, List F, F) -> REC
    rtNormalize        : F -> F
    rootNormalize0     : F -> REC
    rootKernelNormalize : (F, List K, K) -> Union(REC, "failed")
    tanSum             : (F, List F) -> F

    comb?     := F has CombinatorialOpsCategory
    mpiover2 : F := pi()$F / (-2::F)

    realElem(f, l) == rmap(k +-> k2Elem(k, l), f)
    realElementary(f, x) == realElem(f, [x])
    realElementary f     == realElem(f, variables f)
    k_to_liou : K -> F
    k_to_liou1 : (K, SY) -> F
    realLiouvillian(f) == rmap(k_to_liou, f)
    realLiouvillian(f, x) == rmap((k : K) : F +-> k_to_liou1(k, x), f)
    toY ker              == [func for k in ker | (func := ktoY k) ~= 0]
    toZ ker              == [func for k in ker | (func := ktoZ k) ~= 0]
    toU ker              == [func for k in ker | (func := ktoU k) ~= 0]
    toV ker              == [func for k in ker | (func := ktoV k) ~= 0]
    rtNormalize f        == rootNormalize0(f).func
    toR(ker, x) == select(s +-> is?(s, NTHR) and first argument(s) = x, ker)

    -- total Wirtinger derivative allows expressions containing conjugate to be normalized
    -- Wirtinger derivatives:  wdiff(f,x) and wdiff(f,conjugate(x))
    wdiff(ex:F,z:K):F ==
      eval(differentiate(eval(ex,[z],[coerce('%conjugate)]),'%conjugate),[kernel('%conjugate)],[z::F])
    totalDifferentiate(f:F,x:SY):F == wdiff(f,kernel(x))+sqrt(-1)*wdiff(f,kernels(conjugate(coerce x)$FunctionalSpecialFunction(R, F))(1) )

    if R has GcdDomain then
      tanQ(c, x) ==
        tanNa(rootSimp zeroOf tanAn(x, denom(c)::PositiveInteger), numer c)
    else
      tanQ(c, x) ==
        tanNa(zeroOf tanAn(x, denom(c)::PositiveInteger), numer c)

    -- tanSum(c, [a1, ..., an]) returns f(c, a1, ..., an) such that
    -- if ai = tan(ui) then f(c, a1, ..., an) = tan(c + u1 + ... + un).
    -- MUST BE CAREFUL FOR WHEN c IS AN ODD MULTIPLE of pi/2
    tanSum(c, l) ==
      k := c / mpiover2        -- k = - 2 c / pi, check for odd integer
                               -- tan((2n+1) pi/2 x) = - 1 / tan x
      (r := retractIfCan(k)@Union(Z, "failed")) case Z and odd?(r::Z) =>
           - inv tanSum l
      tanSum concat(tan c, l)

    rootNormalize0 f ==
      ker := select!(x +-> is?(x, NTHR) and empty? variables first argument x,
                      tower f)$List(K)
      empty? ker => [f, empty(), empty()]
      (n := (#ker)::Z - 1) < 1 => [f, empty(), empty()]
      for i in 1..n for kk in rest ker repeat
        (u := rootKernelNormalize(f, first(ker, i), kk)) case REC =>
          rec := u::REC
          rn  := rootNormalize0(rec.func)
          return [rn.func, concat(rec.kers, rn.kers), concat(rec.vals, rn.vals)]
      [f, empty(), empty()]

    findQRelation(lv : List Symbol, lpar : List Symbol, lk : List F, _
             ker : F) : U ==

        null lk => [true]
        isconstant := true
        m := #lv
        lvv := lv
        n := #lk
        v := new(m, 0)$(Vector F)
        for i in 1..m for var in lv repeat
            v(i) := totalDifferentiate(ker, var)
            if isconstant then
                isconstant := v(i) = 0
        if isconstant then
            m := #lpar
            lvv := lpar
            v := new(m, 0)$(Vector F)
            for i in 1..m for var in lpar repeat
                v(i) := totalDifferentiate(ker, var)
                if isconstant then
                    isconstant := v(i) = 0
        isconstant =>
            print(ker::OutputForm)$OutputForm
            error "Hidden constant detected"
        mat := new(m, n, 0)$(Matrix F)
        for i in 1..m for var in lvv repeat
            for j in 1..n for k in lk repeat
                mat(i, j) := totalDifferentiate(k, var)
        (u := particularSolutionOverQ(mat, v)) case Vector(Q) => [u::Vector(Q)]
        [true]

    -- This is only correct if Schanuel Conjecture is true, otherwise
    -- we may miss some relations.
    findLinearRelation1(lk : List F, ker : F) : U ==
        null lk => [true]

        n := #lk
        mat := new(1, n, 0)$(Matrix F)
        v := new(1, ker)$(Vector F)
        for j in 1..n for k in lk repeat
            if null(variables(k)) then
                mat(1, j) := k
            else
                mat(1, j) := 0::F
        (u := particularSolutionOverQ(mat, v)) case Vector(Q) => [u::Vector(Q)]
        [true]

    ALGOP  := '%alg
    transkers(x : List K) : List K ==
        [k for k in x | not(has?(operator k, ALGOP))]

    ktoQ(ker : K) : Q ==
       is?(ker, 'log) and F has RetractableTo Q =>
          z : F := argument(ker).1
          qu := retractIfCan(z)@Union(Q, "failed")
          qu case Q => qu::Q
          1
       1

    toQ(lk : List K) : List Q ==
        [ktoQ(k) for k in lk | is?(k, 'log) or is?(k, 'exp)]

    import from MultiplicativeDependence()

    findLinearRelation2(lk : List K, lz : List F, ker : K) : U ==
        z : F := argument(ker).1
        zkers := transkers(kernels(z))
        empty?(zkers) =>
            -- Algebraic case, check for dependencies between logarithms
            -- of rational numbers (we should do better)
            q := ktoQ(ker)
            not(q = 1 or q = -1) =>
                (u := logDependenceQ([toQ (lk)], q)) case Vector(Q) => [u::Vector(Q)]
                [true]
            kerF := ker :: F
            F is Expression(R) and R has ConvertibleTo(Float) _
              and R has IntegralDomain and R has OrderedSet =>
                m := #lz
                for z1 in lz for i in 1..m repeat
                    Fratio : F := kerF/log(z1)
                    (fratio := numericIfCan(Fratio, 20)$Numeric(R) _
                         ) case Float =>
                        qratio := rationalApproximation(fratio::Float, 8)
                        nd : Integer
                        nq : Integer
                        (qratio = 0 or
                          abs(fratio/(qratio::Float)-1.0) > 1.0e-16) _
                          or (abs(nq := numer(qratio)) > 100) _
                          or (abs(nd := denom(qratio)) > 100) => "iterate"
                        kertond := (argument(ker).1)^nd
                        nq > 0 =>
                            lz1tonq := z1^nq
                            (kertond = lz1tonq) =>
                                vv := zero(m)$Vector(Q)
                                qsetelt!(vv, i, qratio)
                                return [vv]
                        lz1tonq := (z1)^(-nq)
                        kertond*lz1tonq = 1 =>
                            vv := zero(m)$Vector(Q)
                            qsetelt!(vv, i, qratio)
                            return [vv]
                [true]
            [true]
        lpars0 : List K := transkers(lk)
        lpars1 : List Symbol := [new()$Symbol for k in lpars0]
        lpars1f : List F := [kernel(s)::F for s in lpars1]
        ly : List F
        nz : F
        if is?(ker, 'log) then
            ly := [log(eval(x, lpars0, lpars1f)) for x in lz]
            nz := log(eval(z, lpars0, lpars1f))
        else
            not(is?(ker, 'atan)) =>
                error "findLinearRelation2: kernel should be log or atan"
            ly := [atan(eval(x, lpars0, lpars1f)) for x in lz]
            nz := atan(eval(z, lpars0, lpars1f))
        findQRelation([], lpars1, ly, nz)

    findRelation(lv : List Symbol, lpar : List Symbol, lk : List K, _
              ker : K) : U ==
        is?(ker, 'log) or is?(ker, 'exp) =>
            null(variables(ker::F)) =>
                is?(ker, 'exp) => findLinearRelation1(toY lk, ktoY ker)
                findLinearRelation2(lk, toZ lk, ker)
            findQRelation(lv, lpar, toY lk, ktoY ker)
        is?(ker, 'atan) or is?(ker, 'tan) =>
            null(variables(ker::F)) =>
                is?(ker, 'tan) => findLinearRelation1(toU lk, ktoU ker)
                findLinearRelation2(lk, toV lk, ker)
            findQRelation(lv, lpar, toU lk, ktoU ker)
        is?(ker, NTHR) => rootDep(lk, ker)
        comb? and is?(ker, 'factorial) =>
            factdeprel([x for x in lk | is?(x, 'factorial) and x ~= ker],
                       ker)
        [true]

    ktoY k ==
      is?(k, 'log) => k::F
      is?(k, 'exp) => first argument k
      0

    ktoZ k ==
      is?(k, 'log) => first argument k
      is?(k, 'exp) => k::F
      0

    ktoU k ==
      is?(k, 'atan) => k::F
      is?(k,  'tan) => first argument k
      0

    ktoV k ==
      is?(k,  'tan) => k::F
      is?(k, 'atan) => first argument k
      0

    smp_map(f : K -> F, p : SMP) : F ==
         map(f, y +-> y::F, p)$PolynomialCategoryLifting(
                                       IndexedExponents K, K, R, SMP, F)

    rmap(f, e) == smp_map(f, numer e)/smp_map(f, denom e)

    LF  ==> LiouvillianFunction(R, F)
    opint : BasicOperator := operator(operator('%iint)$CommonOperators)$LF

    k2Elem0(k : K, op : BasicOperator, args : List F) : F ==
      ez, iez, tz2 : F

      z := first args

      is?(op, POWER)       => (zero? z => 0; exp(last(args) * log z))
      is?(op, 'cot)   => inv tan z
      is?(op, 'acot)  => atan inv z
      is?(op, 'asin)  => atan(z / sqrt(1 - z^2))
      is?(op, 'acos)  => atan(sqrt(1 - z^2) / z)
      is?(op, 'asec)  => atan sqrt(z^2 - 1)
      is?(op, 'acsc)  => atan inv sqrt(z^2 - 1)
      is?(op, 'asinh) => log(sqrt(1 + z^2) + z)
      is?(op, 'acosh) => log(sqrt(z^2 - 1) + z)
      is?(op, 'atanh) => log((z + 1) / (1 - z)) / (2::F)
      is?(op, 'acoth) => log((z + 1) / (z - 1)) / (2::F)
      is?(op, 'asech) => log((inv z) + sqrt(inv(z^2) - 1))
      is?(op, 'acsch) => log((inv z) + sqrt(1 + inv(z^2)))
      is?(op, '%paren) or is?(op, '%box) =>
        empty? rest args => z
        k::F
      if has?(op, HTRIG) then iez  := inv(ez  := exp z)
      is?(op, 'sinh)  => (ez - iez) / (2::F)
      is?(op, 'cosh)  => (ez + iez) / (2::F)
      is?(op, 'tanh)  => (ez - iez) / (ez + iez)
      is?(op, 'coth)  => (ez + iez) / (ez - iez)
      is?(op, 'sech)  => 2 * inv(ez + iez)
      is?(op, 'csch)  => 2 * inv(ez - iez)
      if has?(op, TRIG) then tz2  := tan(z / (2::F))
      is?(op, 'sin)   => 2 * tz2 / (1 + tz2^2)
      is?(op, 'cos)   => (1 - tz2^2) / (1 + tz2^2)
      is?(op, 'sec)   => (1 + tz2^2) / (1 - tz2^2)
      is?(op, 'csc)   => (1 + tz2^2) / (2 * tz2)
      op args

    do_int(op : BasicOperator, args : List(F)) : F ==
        kf1 := op args
        vars := variables(kf1)
        vfs := [v::F for v in vars]
        dvs := [realLiouvillian(D(kf1, v)) for v in vars]
        kernel(opint, concat(vfs, dvs))::F

    k_to_liou(k) ==
        op := operator k
        args := [realLiouvillian(a) for a in argument(k)]
        empty?(args) => k::F
        has?(op, 'prim) and not(is?(op, '%iint)) => do_int(op, args)
        nm := name(op)
        nm = 'polylog and
          (iu := retractIfCan(first(args))@Union(Integer, "failed"))
                 case Integer =>
            (i := iu::Integer) > 0 and i < 10 => do_int(op, args)
            k2Elem0(k, op, args)
        k2Elem0(k, op, args)

    do_int1(op : BasicOperator, args : List(F), x : SY) : F ==
        kf1 := op args
        vars : List(SY) := [x]
        vfs := [v::F for v in vars]
        dvs := [realLiouvillian(D(kf1, v), x) for v in vars]
        kernel(opint, concat(vfs, dvs))::F

    k_to_liou1(k, x) ==
        op := operator k
        args := [realLiouvillian(a, x) for a in argument(k)]
        empty?(args) => k::F
        has?(op, 'prim) and not(is?(op, '%iint)) => do_int1(op, args, x)
        nm := name(op)
        nm = 'Gamma2 and D(first(args), x) = 0 => do_int1(op, args, x)
        nm = 'polylog and
          (iu := retractIfCan(first(args))@Union(Integer, "failed"))
                 case Integer =>
            (i := iu::Integer) > 0 and i < 10 => do_int(op, args)
            k2Elem0(k, op, args)
        (nm = 'ellipticE2 or nm = 'ellipticF) and D(args(2), x) = 0 =>
            do_int1(op, args, x)
        nm = 'ellipticPi and D(args(2), x) = 0 and D(args(3), x) = 0 =>
            do_int1(op, args, x)
        k2Elem0(k, op, args)

    k2Elem(k, l) ==
        op := operator k
        args := [realElem(a, l) for a in argument(k)]
        empty?(args) => k::F
        k2Elem0(k, op, args)

--The next 5 functions are used by normalize, once a relation is found
    depeval(f, lk, k, v) ==
      is?(k, 'log)  => logeval(f, lk, k, v)
      is?(k, 'exp)  => expeval(f, lk, k, v)
      is?(k, 'tan)  => taneval(f, lk, k, v)
      is?(k, 'atan) => ataneval(f, lk, k, v)
      is?(k, NTHR) => rooteval(f, lk, k, v(minIndex v))
      [f, empty(), empty()]

    rooteval(f, lk, k, n) ==
      nv := nthRoot(x := first argument k, m := retract(n)@Z)
      l  := [r for r in concat(k, toR(lk, x)) |
             retract(second argument r)@Z ~= m]
      lv := [nv ^ (n / (retract(second argument r)@Z::Q)) for r in l]
      [eval(f, l, lv), l, lv]

    ataneval(f, lk, k, v) ==
      w := first argument k
      s := tanSum [tanQ(qelt(v, i), x)
                   for i in minIndex v .. maxIndex v for x in toV lk]
      g := +/[qelt(v, i) * x for i in minIndex v .. maxIndex v for x in toU lk]
      h : F :=
        zero?(d := 1 + s * w) => mpiover2
        atan((w - s) / d)
      g := g + h
      [eval(f, [k], [g]), [k], [g]]

    gdCoef?(c, v) ==
      for i in minIndex v .. maxIndex v repeat
        retractIfCan(qelt(v, i) / c)@Union(Z, "failed") case "failed" =>
          return false
      true

    -- If k1 is part of k2 we should not express k1 in terms of k2
    -- (othewise we would get infinite recursion).
    -- Below we impose a stronger condition : we require
    -- height(k1) to be maximal

    goodCoef(v, l, s) ==
      h : NonNegativeInteger := 0
      j : Integer := 0
      ll : List K := []
      for k in l repeat
        if (is?(k, 'log) or is?(k, 'exp)
            or is?(k, 'tan) or is?(k, 'atan)) then
              ll := cons(k, ll)
              h := h + 1
      not (h = (maxIndex(v) - minIndex(v) + 1)) => "failed"
      h := 0
      ll := reverse(ll)
      for i in minIndex v .. maxIndex v for k in ll repeat
        h1 := height(k)
        if (h1 > h) then
          j := i
          h := h1
      for i in minIndex v .. maxIndex v for k in ll repeat
        is?(k, s) and (i >= j) and
           ((r := recip(qelt(v, i))) case Q) and
            (retractIfCan(r::Q)@Union(Z, "failed") case Z)
              and gdCoef?(qelt(v, i), v) => return([i, k])
      "failed"

    taneval(f, lk, k, v) ==
      u := first argument k
      fns := toU lk
      c := u - +/[qelt(v, i) * x for i in minIndex v .. maxIndex v for x in fns]
      (rec := goodCoef(v, lk, 'tan)) case "failed" =>
          tannosimp(f, lk, k, v, fns, c)
      v0 := retract(inv qelt(v, rec.index))@Z
      lv := [qelt(v, i) for i in minIndex v .. maxIndex v |
                                                 i ~= rec.index]$List(Q)
      l  := [kk for kk in lk | kk ~= rec.ker]
      g := tanSum(-v0 * c, concat(tanNa(k::F, v0),
           [tanNa(x, - retract(a * v0)@Z) for a in lv for x in toV l]))
      [eval(f, [rec.ker], [g]), [rec.ker], [g]]

    tannosimp(f, lk, k, v, fns, c) ==
      n := maxIndex v
      lk := [x for x in lk | is?(x, 'tan) or is?(x, 'atan)]
      lk1 := [x for x in lk for i in 1..n | not(qelt(v, i) = 0)]
      every?(x +-> is?(x, 'tan), lk1) =>
        dd := (d := (cd := splitDenominator v).den)::F
        newt := [tan(u / dd) for u in fns
                    for i in 1..n | not(qelt(v, i) = 0)]$List(F)
        newtan := [tanNa(t, d) for t in newt]$List(F)
        li := [i for i in 1..n | not(qelt(v, i) = 0)]
        h := tanSum(c, [tanNa(t, qelt(cd.num, i))
                        for i in li for t in newt])
        newtan := concat(h, newtan)
        lk1 := concat(k, lk1)
        [eval(f, lk1, newtan), lk1, newtan]
      h := tanSum(c, [tanQ(qelt(v, i), x)
                      for i in 1..n for x in toV lk])
      [eval(f, [k], [h]), [k], [h]]

    expnosimp(f, lk, k, v, fns, g) ==
      n := maxIndex v
      lk := [x for x in lk | is?(x, 'exp) or is?(x, 'log)]
      lk1 := [x for x in lk for i in 1..n | not(qelt(v, i) = 0)]
      every?(x +-> is?(x, 'exp), lk1) =>
        dd := (d := (cd := splitDenominator v).den)::F
        newe := [exp(y / dd) for y in fns
                    for i in 1..n | not(qelt(v, i) = 0)]$List(F)
        newexp := [e ^ d for e in newe]$List(F)
        li := [i for i in 1..n | not(qelt(v, i) = 0)]
        h := */[e ^ qelt(cd.num, i)
                for i in li for e in newe] * g
        lk1 := concat(k, lk1)
        newexp := concat(h, newexp)
        [eval(f, lk1, newexp), lk1, newexp]
      h := */[exp(y) ^ qelt(v, i)
                for i in minIndex v .. maxIndex v for y in fns] * g
      [eval(f, [k], [h]), [k], [h]]

    logeval(f, lk, k, v) ==
      z := first argument k
      dd := lcm([denom(qelt(v, i))$Q for i in minIndex v .. maxIndex v
                ]$List(Z))
      c := z^dd / (*/[x^(dd*qelt(v, i))
                   for x in toZ lk for i in minIndex v .. maxIndex v])
-- CHANGED log ktoZ x TO ktoY x SINCE WE WANT log exp f TO BE REPLACED BY f.
      g := +/[qelt(v, i) * x
              for i in minIndex v .. maxIndex v for x in toY lk]
                + log(c)/(dd::R::F)
      [eval(f, [k], [g]), [k], [g]]

    rischNormalize(f : F, vars : List SY) : REC ==
      lk : List K := tower f
      funs := lk -- [k for k in lk | height k > 1]@(List K)
      pars := variables(f) -- [name(operator(k)) for k in lk | height k = 1]
      pars := setDifference(pars, vars)
      --  funs := [k for k in kers | height k > 1]
      empty?(funs) => [f, empty(), empty()]
      n := #funs

      for i in 1..n for kk in rest funs repeat
        klist := first(funs, i)
        -- NO EVALUATION ON AN EMPTY VECTOR, WILL CAUSE INFINITE LOOP
        (c := findRelation(vars, pars, klist, kk)) case vec and not empty?(c.vec) =>

          rec := depeval(f, klist, kk, c.vec)
          rn  := rischNormalize(rec.func, vars)
          return [rn.func,
                   concat(rec.kers, rn.kers), concat(rec.vals, rn.vals)]
        c case func =>
          rn := rischNormalize(eval(f, [kk], [c.func]), vars)
          return [rn.func, concat(kk, rn.kers), concat(c.func, rn.vals)]
      [f, empty(), empty()]

    rischNormalize(f : F, v : SY) : REC == rischNormalize(f, [v])

    rootNormalize(f, k) ==
      (u := rootKernelNormalize(f, toR(tower f, first argument k), k))
         case "failed" => f
      (u::REC).func

    rootKernelNormalize(f, l, k) ==
      (c := rootDep(l, k)) case vec =>
        rooteval(f, l, k, (c.vec)(minIndex(c.vec)))
      "failed"

    localnorm f == rischNormalize(f, []).func

    validExponential(twr, eta, x) ==
      (c := particularSolutionOverQ(construct([totalDifferentiate(g, x)
         for g in (fns := toY twr)]$List(F))@Vector(F),
           totalDifferentiate(eta, x))) case "failed" => "failed"
      v := c::Vector(Q)
      g := eta - +/[qelt(v, i) * yy
                        for i in minIndex v .. maxIndex v for yy in fns]
      */[exp(yy) ^ qelt(v, i)
                for i in minIndex v .. maxIndex v for yy in fns] * exp g

    if R has GcdDomain then
      import from PolynomialRoots(IndexedExponents K, K, R, P, F)
      irootDep(k : K) : U ==
         n : N := (retract(second argument k)@Z)::N
         pr := froot(first argument k, n)
         not(pr.coef = 1) or not(pr.exponent = n) =>
             pr.exponent = 1 => [pr.coef*pr.radicand]
             nf : F := (pr.exponent)::F
             nr : F := pr.radicand
             nk : F := kernel(operator k, [nr, nf])
             nv : F := pr.coef*nk
             [nv]
         [true]
    else
      irootDep(k : K) : U == [true]

    rootDep(ker, k) ==
      empty?(ker := toR(ker, first argument k)) => irootDep(k)
      [new(1, lcm(retract(second argument k)@Z,
       "lcm"/[retract(second argument r)@Z for r in ker])::Q)$Vector(Q)]

    expeval(f, lk, k, v) ==
      y   := first argument k
      fns := toY lk
      g := y - +/[qelt(v, i) * z for i in minIndex v .. maxIndex v for z in fns]
      (rec := goodCoef(v, lk, 'exp)) case "failed" =>
        expnosimp(f, lk, k, v, fns, exp g)
      v0 := retract(inv qelt(v, rec.index))@Z
      lv := [qelt(v, i) for i in minIndex v .. maxIndex v |
                                                 i ~= rec.index]$List(Q)
      l  := [kk for kk in lk | kk ~= rec.ker]
      h : F := */[exp(z) ^ (- retract(a * v0)@Z) for a in lv for z in toY l]
      h := h * exp(-v0 * g) * (k::F) ^ v0
      [eval(f, [rec.ker], [h]), [rec.ker], [h]]

    if F has CombinatorialOpsCategory then
      normalize f == rtNormalize localnorm factorials realElementary f

      normalize(f, x) ==
        rtNormalize(rischNormalize(factorials(realElementary(f, x), x), x).func)

      factdeprel(l, k) ==
        ((r := retractIfCan(n := first argument k)@Union(Z, "failed"))
          case Z) and (r::Z > 0) => [factorial(r::Z)::F]
        for x in l repeat
          m := first argument x
          ((r := retractIfCan(n - m)@Union(Z, "failed")) case Z) =>
            (r::Z > 0) => return([*/[(m + i::F) for i in 1..r] * x::F])
            error "bad order of factorials"
        [true]

    else
      normalize f     == rtNormalize localnorm realElementary f
      normalize(f, x) == rtNormalize(rischNormalize(realElementary(f, x), x).func)

spad

   Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/4918645116496175848-25px002.spad
      using old system compiler.
   EFSTRUX abbreviates package ElementaryFunctionStructurePackage 
------------------------------------------------------------------------
   initializing NRLIB EFSTRUX for ElementaryFunctionStructurePackage 
   compiling into NRLIB EFSTRUX 
****** Domain: R already in scope
****** Domain: R already in scope
****** Domain: R already in scope
****** Domain: F already in scope
****** Domain: F already in scope
   importing TangentExpansions F
   importing IntegrationTools(R,F)
   importing IntegerLinearDependence F
   importing AlgebraicManipulations(R,F)
   importing InnerCommonDenominator(Integer,Fraction Integer,Vector Integer,Vector Fraction Integer)
   processing macro definition P ==> SparseMultivariatePolynomial(R,Kernel F) 
****** Domain: F already in scope
augmenting F: (CombinatorialOpsCategory)
   compiling local realElem : (F,List Symbol) -> F
Time: 0.04 SEC.

   compiling exported realElementary : (F,Symbol) -> F
Time: 0.01 SEC.

   compiling exported realElementary : F -> F
Time: 0 SEC.

   compiling exported realLiouvillian : F -> F
Time: 0 SEC.

   compiling exported realLiouvillian : (F,Symbol) -> F
Time: 0 SEC.

   compiling local toY : List Kernel F -> List F
Time: 0 SEC.

   compiling local toZ : List Kernel F -> List F
Time: 0 SEC.

   compiling local toU : List Kernel F -> List F
Time: 0 SEC.

   compiling local toV : List Kernel F -> List F
Time: 0.01 SEC.

   compiling local rtNormalize : F -> F
Time: 0 SEC.

   compiling local toR : (List Kernel F,F) -> List Kernel F
Time: 0.02 SEC.

   compiling local wdiff : (F,Kernel F) -> F
Time: 0 SEC.

   compiling local totalDifferentiate : (F,Symbol) -> F
Time: 0.02 SEC.

****** Domain: R already in scope
augmenting R: (GcdDomain)
   compiling exported tanQ : (Fraction Integer,F) -> F
Time: 0.01 SEC.

   compiling exported tanQ : (Fraction Integer,F) -> F
Time: 0 SEC.

   compiling local tanSum : (F,List F) -> F
Time: 0 SEC.

   compiling local rootNormalize0 : F -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.02 SEC.

   compiling local findQRelation : (List Symbol,List Symbol,List F,F) -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0.07 SEC.

   compiling local findLinearRelation1 : (List F,F) -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0.03 SEC.

   compiling local transkers : List Kernel F -> List Kernel F
Time: 0 SEC.

   compiling local ktoQ : Kernel F -> Fraction Integer
Time: 0.01 SEC.

   compiling local toQ : List Kernel F -> List Fraction Integer
Time: 0 SEC.

   importing MultiplicativeDependence
   compiling local findLinearRelation2 : (List Kernel F,List F,Kernel F) -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
****** Domain: R already in scope
augmenting R: (ConvertibleTo (Float))
****** Domain: R already in scope
augmenting R: (OrderedSet)
Time: 0.75 SEC.

   compiling local findRelation : (List Symbol,List Symbol,List Kernel F,Kernel F) -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0.02 SEC.

   compiling local ktoY : Kernel F -> F
Time: 0 SEC.

   compiling local ktoZ : Kernel F -> F
Time: 0 SEC.

   compiling local ktoU : Kernel F -> F
Time: 0 SEC.

   compiling local ktoV : Kernel F -> F
Time: 0 SEC.

   compiling local smp_map : (Kernel F -> F,SparseMultivariatePolynomial(R,Kernel F)) -> F
Time: 0 SEC.

   compiling exported rmap : (Kernel F -> F,F) -> F
Time: 0 SEC.

   processing macro definition LF ==> LiouvillianFunction(R,F) 
   compiling local k2Elem0 : (Kernel F,BasicOperator,List F) -> F
Time: 0.15 SEC.

   compiling local do_int : (BasicOperator,List F) -> F
Time: 0.01 SEC.

   compiling local k_to_liou : Kernel F -> F
Time: 0.01 SEC.

   compiling local do_int1 : (BasicOperator,List F,Symbol) -> F
Time: 0.01 SEC.

   compiling local k_to_liou1 : (Kernel F,Symbol) -> F
Time: 0.06 SEC.

   compiling local k2Elem : (Kernel F,List Symbol) -> F
Time: 0 SEC.

   compiling local depeval : (F,List Kernel F,Kernel F,Vector Fraction Integer) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.01 SEC.

   compiling local rooteval : (F,List Kernel F,Kernel F,Fraction Integer) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.08 SEC.

   compiling local ataneval : (F,List Kernel F,Kernel F,Vector Fraction Integer) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.05 SEC.

   compiling local gdCoef? : (Fraction Integer,Vector Fraction Integer) -> Boolean
Time: 0.01 SEC.

   compiling local goodCoef : (Vector Fraction Integer,List Kernel F,Symbol) -> Union(Record(index: Integer,ker: Kernel F),failed)
Time: 0.03 SEC.

   compiling local taneval : (F,List Kernel F,Kernel F,Vector Fraction Integer) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.03 SEC.

   compiling local tannosimp : (F,List Kernel F,Kernel F,Vector Fraction Integer,List F,F) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.03 SEC.

   compiling local expnosimp : (F,List Kernel F,Kernel F,Vector Fraction Integer,List F,F) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.19 SEC.

   compiling local logeval : (F,List Kernel F,Kernel F,Vector Fraction Integer) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.09 SEC.

   compiling exported rischNormalize : (F,List Symbol) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.01 SEC.

   compiling exported rischNormalize : (F,Symbol) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0 SEC.

   compiling exported rootNormalize : (F,Kernel F) -> F
Time: 0.01 SEC.

   compiling local rootKernelNormalize : (F,List Kernel F,Kernel F) -> Union(Record(func: F,kers: List Kernel F,vals: List F),failed)
Time: 0 SEC.

   compiling local localnorm : F -> F
Time: 0 SEC.

   compiling exported validExponential : (List Kernel F,F,Symbol) -> Union(F,failed)
Time: 0.06 SEC.

****** Domain: R already in scope
augmenting R: (GcdDomain)
   importing PolynomialRoots(IndexedExponents Kernel F,Kernel F,R,SparseMultivariatePolynomial(R,Kernel F),F)
   compiling exported irootDep : Kernel F -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0.03 SEC.

   compiling exported irootDep : Kernel F -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0 SEC.

   compiling local rootDep : (List Kernel F,Kernel F) -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0.03 SEC.

   compiling local expeval : (F,List Kernel F,Kernel F,Vector Fraction Integer) -> Record(func: F,kers: List Kernel F,vals: List F)
Time: 0.09 SEC.

   compiling exported normalize : F -> F
Time: 0.01 SEC.

   compiling exported normalize : (F,Symbol) -> F
Time: 0 SEC.

   compiling local factdeprel : (List Kernel F,Kernel F) -> Union(vec: Vector Fraction Integer,func: F,fail: Boolean)
Time: 0.03 SEC.

   compiling exported normalize : F -> F
Time: 0 SEC.

   compiling exported normalize : (F,Symbol) -> F
Time: 0 SEC.

(time taken in buildFunctor:  0)

;;;     ***       |ElementaryFunctionStructurePackage| REDEFINED

;;;     ***       |ElementaryFunctionStructurePackage| REDEFINED
Time: 0 SEC.

   Warnings: 
      [1] rtNormalize:  func has no value
      [2] rootNormalize0:  func has no value
      [3] rootNormalize0:  kers has no value
      [4] rootNormalize0:  vals has no value
      [5] findLinearRelation2:  nd has no value
      [6] findLinearRelation2:  nq has no value
      [7] findLinearRelation2:  ly has no value
      [8] findLinearRelation2:  nz has no value
      [9] k2Elem0:  ez has no value
      [10] k2Elem0:  iez has no value
      [11] k2Elem0:  tz2 has no value
      [12] goodCoef:  h has no value
      [13] goodCoef:  ll has no value
      [14] goodCoef:  j has no value
      [15] taneval:  ker has no value
      [16] tannosimp:  den has no value
      [17] tannosimp:  num has no value
      [18] expnosimp:  den has no value
      [19] expnosimp:  num has no value
      [20] logeval:  STEP has no value
      [21] logeval:  i has no value
      [22] rischNormalize:  vec has no value
      [23] rischNormalize:  func has no value
      [24] rischNormalize:  kers has no value
      [25] rischNormalize:  vals has no value
      [26] rootNormalize:  func has no value
      [27] rootKernelNormalize:  vec has no value
      [28] validExponential:  IN has no value
      [29] validExponential:  g has no value
      [30] irootDep:  coef has no value
      [31] irootDep:  exponent has no value
      [32] irootDep:  radicand has no value
      [33] expeval:  ker has no value

   Cumulative Statistics for Constructor ElementaryFunctionStructurePackage
      Time: 2.04 seconds

   finalizing NRLIB EFSTRUX 
   Processing ElementaryFunctionStructurePackage for Browser database:
--------constructor---------
--------(normalize (F F))---------
--------(normalize (F F (Symbol)))---------
--------(rischNormalize ((Record (: func F) (: kers (List (Kernel F))) (: vals (List F))) F (Symbol)))---------
--------(rischNormalize ((Record (: func F) (: kers (List (Kernel F))) (: vals (List F))) F (List (Symbol))))---------
--------(realElementary (F F))---------
--------(realLiouvillian (F F))---------
--------(realLiouvillian (F F (Symbol)))---------
--------(realElementary (F F (Symbol)))---------
--------(validExponential ((Union F failed) (List (Kernel F)) F (Symbol)))---------
--------(rootNormalize (F F (Kernel F)))---------
--------(rmap (F (Mapping F (Kernel F)) F))---------
--------(tanQ (F (Fraction (Integer)) F))---------
--------(irootDep ((Union (: vec (Vector (Fraction (Integer)))) (: func F) (: fail (Boolean))) (Kernel F)))---------
; compiling file "/var/aw/var/LatexWiki/EFSTRUX.NRLIB/EFSTRUX.lsp" (written 16 SEP 2014 03:35:47 AM):

; /var/aw/var/LatexWiki/EFSTRUX.NRLIB/EFSTRUX.fasl written
; compilation finished in 0:00:00.694
------------------------------------------------------------------------
   ElementaryFunctionStructurePackage is now explicitly exposed in 
      frame initial 
   ElementaryFunctionStructurePackage will be automatically loaded when
      needed from /var/aw/var/LatexWiki/EFSTRUX.NRLIB/EFSTRUX

Tests

normalize is supposed to rewrite the expression using the least possible number of independent kernels

fricas

ex1:Expression Complex Integer:=exp(conjugate(x)+x)+exp(x) + exp(conjugate(x))

$\label{eq1}{{e}^{{\overline x}+ x}}+{{e}^{\overline x}}+{{e}^{x}}$

(1)

Type: Expression(Complex(Integer))

fricas

kernels ex1

$\label{eq2}\left[{{e}^{{\overline x}+ x}}, \:{{e}^{\overline x}}, \:{{e}^{x}}\right]$

(2)

Type: List(Kernel(Expression(Complex(Integer))))

fricas

ex2:=normalize(ex1)

$\label{eq3}{{{\left({{e}^{x}}+ 1 \right)}\ {{e}^{{\overline x}+ x}}}+{{{e}^{x}}^{2}}}\over{{e}^{x}}$

(3)

Type: Expression(Complex(Integer))

fricas

kernels ex2

$\label{eq4}\left[{{e}^{{\overline x}+ x}}, \:{{e}^{x}}\right]$

(4)

Type: List(Kernel(Expression(Complex(Integer))))

fricas

simplify(ex1-ex2)

$\label{eq5}0$

(5)

Type: Expression(Complex(Integer))

fricas

eval(ex1,x=complex(1,1))

$\label{eq6}{{e}^{2}}+{{e}^{1 + i}}+{{e}^{1 - i}}$

(6)

Type: Expression(Complex(Integer))

fricas

complexNumeric %

$\label{eq7}10.3264439787_62420542$

(7)

Type: Complex(Float)

fricas

eval(ex2,x=complex(1,1))

$\label{eq8}{{{\left({{e}^{1 + i}}+ 1 \right)}\ {{e}^{2}}}+{{{e}^{1 + i}}^{2}}}\over{{e}^{1 + i}}$

(8)

Type: Expression(Complex(Integer))

fricas

complexNumeric %

$\label{eq9}10.3264439787_62420542$

(9)

Type: Complex(Float)

fricas

normalize(ex1-ex2)

$\label{eq10}0$

(10)

Type: Expression(Complex(Integer))

fricas

ex3:Expression Complex Integer:=tan(conjugate(x)+x)+tan(x) + tan(conjugate(x))

$\label{eq11}{\tan \left({{\overline x}+ x}\right)}+{\tan \left({\overline x}\right)}+{\tan \left({x}\right)}$

(11)

Type: Expression(Complex(Integer))

fricas

kernels ex3

$\label{eq12}\left[{\tan \left({{\overline x}+ x}\right)}, \:{\tan \left({\overline x}\right)}, \:{\tan \left({x}\right)}\right]$

(12)

Type: List(Kernel(Expression(Complex(Integer))))

fricas

ex4:=normalize(ex3)

$\label{eq13}{{{\tan \left({x}\right)}\ {{\tan \left({{\overline x}+ x}\right)}^{2}}}+{{\left({{\tan \left({x}\right)}^{2}}+ 2 \right)}\ {\tan \left({{\overline x}+ x}\right)}}}\over{{{\tan \left({x}\right)}\ {\tan \left({{\overline x}+ x}\right)}}+ 1}$

(13)

Type: Expression(Complex(Integer))

fricas

kernels ex4

$\label{eq14}\left[{\tan \left({{\overline x}+ x}\right)}, \:{\tan \left({x}\right)}\right]$

(14)

Type: List(Kernel(Expression(Complex(Integer))))

fricas

simplify(ex3-ex4)

$\label{eq15}{\left( \begin{array}{@{}l} \displaystyle {{\left({{\sin \left({x}\right)}\ {\sin \left({\overline x}\right)}}-{{\cos \left({x}\right)}\ {\cos \left({\overline x}\right)}}\right)}\ {\sin \left({{\overline x}+ x}\right)}}+ \ \ \displaystyle {{\cos \left({x}\right)}\ {\cos \left({{\overline x}+ x}\right)}\ {\sin \left({\overline x}\right)}}+{{\sin \left({x}\right)}\ {\cos \left({\overline x}\right)}\ {\cos \left({{\overline x}+ x}\right)}}$

(15)

Type: Expression(Complex(Integer))

fricas

complexElementary %

$\label{eq16}{{2 \ i \ {{{e}^{{i \ {\overline x}}+{i \ x}}}^{2}}}-{2 \ i \ {{{e}^{i \ x}}^{2}}\ {{{e}^{i \ {\overline x}}}^{2}}}}\over{{{\left({{{e}^{i \ {\overline x}}}^{2}}+ 1 \right)}\ {{{e}^{{i \ {\overline x}}+{i \ x}}}^{2}}}+{{{{e}^{i \ x}}^{2}}\ {{{e}^{i \ {\overline x}}}^{2}}}+{{{e}^{i \ x}}^{2}}}$

(16)

Type: Expression(Complex(Integer))

fricas

simplify %

$\label{eq17}0$

(17)

Type: Expression(Complex(Integer))

fricas

eval(ex3,x=complex(1,1))

$\label{eq18}{\tan \left({2}\right)}+{\tan \left({1 + i}\right)}+{\tan \left({1 - i}\right)}$

(18)

Type: Expression(Complex(Integer))

fricas

complexNumeric %

$\label{eq19}-{1.6415346926_224955586}$

(19)

Type: Complex(Float)

fricas

eval(ex4,x=complex(1,1))

$\label{eq20}{{{\tan \left({1 + i}\right)}\ {{\tan \left({2}\right)}^{2}}}+{{\left({{\tan \left({1 + i}\right)}^{2}}+ 2 \right)}\ {\tan \left({2}\right)}}}\over{{{\tan \left({1 + i}\right)}\ {\tan \left({2}\right)}}+ 1}$

(20)

Type: Expression(Complex(Integer))

fricas

complexNumeric %

$\label{eq21}-{1.6415346926_224955586}+{{0.3 E - 20}\ i}$

(21)

Type: Complex(Float)

fricas

normalize(ex3-ex4)

$\label{eq22}0$

(22)

Type: Expression(Complex(Integer))

integration --Bill Page, Tue, 16 Sep 2014 02:42:58 +0000 reply

fricas

)lib FSPECX EFSTRUX

   FunctionalSpecialFunction is already explicitly exposed in frame 
      initial 
   FunctionalSpecialFunction will be automatically loaded when needed 
      from /var/aw/var/LatexWiki/FSPECX.NRLIB/FSPECX
   ElementaryFunctionStructurePackage is already explicitly exposed in 
      frame initial 
   ElementaryFunctionStructurePackage will be automatically loaded when
      needed from /var/aw/var/LatexWiki/EFSTRUX.NRLIB/EFSTRUX

fricas