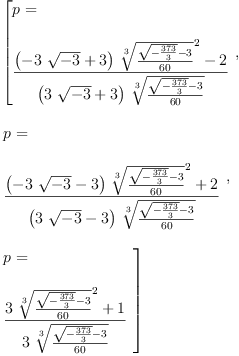This page is set to execute \begin{axiom}... \end{axiom}
commands using FriCAS. See also FriCASIntegration.
fricas
(1) -> )version
"FriCAS 1.3.10 compiled at Wed 10 Jan 02:19:45 CET 2024"
Any comments added here use this version of FriCAS.
fricas
solve(s=v*t+a*t^2/2,t)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
radicalSolve(s=v*t+a*t^2/2,t)
Type: List(Equation(Expression(Integer)))
fricas
solve(v*t+a*t^2/2-s=0,t)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
solve(v*t+a*t/2-s=0,t)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
solve(v*t+a*t^2/2-s=0,t)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
radicalSolve(p^3 - p + 1/10=0,p)
Type: List(Equation(Expression(Integer)))
fricas
R1 ==> Record(foo1: String, remLexs: List Integer)
Type: Void
fricas
R2 ==> Record(foo2: String, remLexs: List Integer)
Type: Void
fricas
r1: R1 := ["a", [1,2,3]]
Type: Record(foo1: String,remLexs: List(Integer))
fricas
r2: R2 := ["b", [5]]
Type: Record(foo2: String,remLexs: List(Integer))
fricas
r1.remLexs
Type: List(Integer)
fricas
r2.remLexs
Type: List(Integer)
fricas
)set output tex off
fricas
)set output algebra on
guessPRec [1, 0, 1, 1, 4, 10, 35, 120, 455, 1792, 7413, 31780, 140833, 641928, 3000361, 14338702, 69902535, 346939792, 1750071307, 8958993507, 46484716684, 244187539270, 1297395375129, 6965930587924]
(13)
[
[
f(n):
2 2
(- n - 17 n - 72)f(n + 3) + (4 n + 30 n + 44)f(n + 2)
+
2 2
(19 n + 113 n + 150)f(n + 1) + (14 n + 42 n + 28)f(n)
=
0
,
f(0) = 1, f(1) = 0, f(2) = 1]
]
Type: List(Expression(Integer))
fricas
guessRec([1,1,0,1,- 1,2,- 1,5,- 4,29,- 13,854,- 685])
2
(14) [[f(n): f(n + 2) + f(n + 1) - f(n) = 0, f(0) = 1, f(1) = 1]]
Type: List(Expression(Integer))
fricas
integrate(exp(x-x^2), x)
1
-
4 2 x - 1 +---+
%e erf(-------)\|%pi
2
(15) ---------------------
2
Type: Union(Expression(Integer),...)
fricas
1+1
(16) 2
2^3-2**3
2^3
fricas
2^3
(17) 8
fricas
2**3
There are no library operations named **
Use HyperDoc Browse or issue
)what op **
to learn if there is any operation containing " ** " in its name.
Cannot find a definition or applicable library operation named **
with argument type(s)
PositiveInteger
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
sqrt(2)^2-2
(18) 0
fricas
a:=sqrt(2)
+-+
(19) \|2
fricas
b:=sqrt(a)
+----+
| +-+
(20) \|\|2
fricas
b^2-a
(21) 0
fricas
f(a) == { local b=sqrt(a); b^2-a}
Line 1: f(a) == { local b=sqrt(a); b^2-a}
........A........B
Error A: Missing mate.
Error B: syntax error at top level
Error B: Possibly missing a }
3 error(s) parsing
local needs to be on separate statement:
fricas
f(a) == { local b; b :=sqrt(a); b^2-a}
Type: Void
fricas
f(2)
fricas
Compiling function f with type PositiveInteger -> AlgebraicNumber
(23) 0
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
(24) 0
fricas
[q,r]
(25) [q, r]
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(2)
fricas
Compiling function f with type PositiveInteger -> AlgebraicNumber
(27) 0
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
(28) 0
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(2)
fricas
Compiling function f with type PositiveInteger -> AlgebraicNumber
(30) 0
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
(31) 0
fricas
f(z)
fricas
Compiling function f with type Variable(z) -> Expression(Integer)
(32) 0
Type: Expression(Integer)
fricas
f(%i)
fricas
Compiling function f with type Complex(Integer) -> Expression(
Complex(Integer))
(33) 0Type: Expression(Complex(Integer))
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(2)
fricas
Compiling function f with type PositiveInteger -> AlgebraicNumber
(35) 0
fricas
c:=f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
(36) 0
fricas
)display properties c
Properties of c :
Value (has type AlgebraicNumber): 0
fricas
f(a) == ( local b; b:=sqrt(a); b^2 = a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(a) == ( local b; b:=sqrt(a); b^2 = a)
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(2)
fricas
Compiling function f with type PositiveInteger -> Equation(
AlgebraicNumber)
(39) 2 = 2Type: Equation(AlgebraicNumber
?)
fricas
f(%i)
fricas
Compiling function f with type Complex(Integer) -> Equation(
Expression(Complex(Integer)))
(40) %i = %iType: Equation(Expression(Complex(Integer)))
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> Equation(
AlgebraicNumber)
+-+ +-+
(41) \|2 = \|2Type: Equation(AlgebraicNumber
?)
fricas
f(2^(1/2))
+-+ +-+
(42) \|2 = \|2
Type: Equation(AlgebraicNumber
?)
fricas
f(2^(1/3))
3+-+ 3+-+
(43) \|2 = \|2
Type: Equation(AlgebraicNumber
?)
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
(45) 0
fricas
)set output fortran
--------------------------- The fortran Option ----------------------------
Description: create output in FORTRAN format
)set output fortran is used to tell FriCAS to turn FORTRAN-style output
printing on and off, and where to place the output. By default, the
destination for the output is the screen but printing is turned off.
Syntax: )set output fortran <arg>
where arg can be one of
on turn FORTRAN printing on
off turn FORTRAN printing off (default state)
console send FORTRAN output to screen (default state)
fp<.fe> send FORTRAN output to file with file prefix fp and file
extension .fe. If not given, .fe defaults to .sfort.
If you wish to send the output to a file, you may need to issue this command
twice: once with on and once with the file name. For example, to send
FORTRAN output to the file polymer.sfort, issue the two commands
)set output fortran on
)set output fortran polymer
The output is placed in the directory from which you invoked FriCAS or
the one you set with the )cd system command.
The current setting is: Off:CONSOLE
f(sqrt(2))
(46) 0
fricas
)set output tex
----------------------------- The tex Option ------------------------------
Description: create output in TeX style
)set output tex is used to tell FriCAS to turn TeX-style output
printing on and off, and where to place the output. By default, the
destination for the output is the screen but printing is turned off.
Syntax: )set output tex <arg>
where arg can be one of
on turn TeX printing on
off turn TeX printing off (default state)
console send TeX output to screen (default state)
fp<.fe> send TeX output to file with file prefix fp and file
extension .fe. If not given, .fe defaults to .stex.
If you wish to send the output to a file, you may need to issue this command
twice: once with on and once with the file name. For example, to send
TeX output to the file polymer.stex, issue the two commands
)set output tex on
)set output tex polymer
The output is placed in the directory from which you invoked FriCAS or
the one you set with the )cd system command.
The current setting is: Off:CONSOLE
f(sqrt(2))
(47) 0
fricas
)set output script
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
f(sqrt(2))
(48) 0
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
(50) 0
fricas
)set output fortran on
f(sqrt(2))
R51=0
(51) 0
fricas
)set output tex on
f(sqrt(2))
R52=0
(52) 0
fricas
)set output script on
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
Your value on is not among the valid choices.
f(sqrt(2))
R53=0
(53) 0
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
R55=0
(55) 0
fricas
)set output fortran console
f(sqrt(2))
R56=0
(56) 0
fricas
)set output tex console
f(sqrt(2))
R57=0
(57) 0
fricas
)set output script console
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
Your value console is not among the valid choices.
f(sqrt(2))
R58=0
(58) 0
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
R60=0
(60) 0
fricas
)set output fortran on
fricas
)set output fortran console
f(sqrt(2))
R61=0
(61) 0
fricas
)set output tex on
fricas
)set output tex console
f(sqrt(2))
R62=0
(62) 0
fricas
)set output script on
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
Your value on is not among the valid choices.
fricas
)set output script console
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
Your value console is not among the valid choices.
f(sqrt(2))
R63=0
(63) 0
fricas
f(a) == ( local b; b:=sqrt(a); b^2-a)
Compiled code for f has been cleared.
1 old definition(s) deleted for function or rule f
Type: Void
fricas
f(sqrt(2))
fricas
Compiling function f with type AlgebraicNumber -> AlgebraicNumber
R65=0
(65) 0
fricas
)set output fortran on
f(sqrt(2))
R66=0
(66) 0
fricas
)set output fortran off
fricas
)set output tex on
f(sqrt(2))
(67) 0
fricas
)set output tex off
fricas
)set output script on
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
Your value on is not among the valid choices.
f(sqrt(2))
(68) 0
fricas
)set output script off
--------------------------- The scripts Option ----------------------------
Description: show subscripts,... linearly
The scripts option may be followed by any one of the following:
yes
no
The current setting is indicated within the list.
Your value off is not among the valid choices.
((1+2)/3)::SquareMatrix
?(3,Integer)
fricas
((1+2)/3)::SquareMatrix(3,Integer)
+1 0 0+
| |
(69) |0 1 0|
| |
+0 0 1+
Type: SquareMatrix
?(3,
Integer)
fricas
((1+2)/3)::SquareMatrix(3,Integer)
+1 0 0+
| |
(70) |0 1 0|
| |
+0 0 1+
Type: SquareMatrix
?(3,
Integer)
fricas
integrate((x+sin(x))^(1/2), x)
>> Error detected within library code:
integrate: implementation incomplete (has polynomial part)
fricas
integrate((x+sin(x))^(1/2), x)
>> Error detected within library code:
integrate: implementation incomplete (has polynomial part)
fricas
"";
"Notice how the CAS computes the second (displayed) integral, while saying 'proved non-elementary' about the first one,";
"despite the fact that the two are equal for any x in [-1..-1/sqrt(2)].";
"My guess is that the system does not apply transformations that force additional restrictions on the function domain...";
"Notice also how transforming the integrand into a form that the CAS can find an elementary antiderivative for requires";
"quite some discipline in keeping track of the integrand domain, as well as using some not-so-obvious transfromations...";
t:=sqrt(1-x*x);
nume:=(acos(x)*t)^(-1);
deno:=log(2*acos(x)/%pi);
transformedDeno:=log(2+asin(2*x*t)/%pi);
failedIntegral:=integrate(nume/transformedDeno,x);
integrate(nume/deno, x)
2 acos(x)
(71) - log(log(---------))
%pi
Type: Union(Expression(Integer),...)
fricas
integrate((x+sin(x))^(1/3),x)
>> Error detected within library code:
integrate: implementation incomplete (has polynomial part)
fricas
t:=x+log(x);
nume:=(x^2+x+1)*sqrt(t)+(3*x+1)*log(x)+3*x*x+x;
deno:=x*t*sqrt(t)+x*x*t;
check:=integrate(nume/deno,x);
differentiate(2*sqrt(t)+2*log(x+sqrt(t)), x)
2 +----------+ 2
(x + 2 x + 1)\|log(x) + x + (3 x + 1)log(x) + 3 x + x
(72) --------------------------------------------------------
2 +----------+ 2 3
(x log(x) + x )\|log(x) + x + x log(x) + x
Type: Expression(Integer)
No lie, compare:
fricas
nume - numer(differentiate(2*sqrt(t)+2*log(x+sqrt(t)), x))
+----------+
(73) - x\|log(x) + x
Type: Expression(Integer)
Still, shame that FriCAS can not do corrected example...
fricas
nume:= 3*(x+exp(x))^(1/3)+(2*x*x+3*x)*exp(x)+5*x*x;
deno:= x*(x+exp(x))^(1/3);
"integrate(nume/deno, x)"
(q:=nume/deno, differentiate(3*x*(x+exp(x))^(2/3)+3*log(x), x))
(74)
+-------+
3| x 2 x 2
3 \|%e + x + (2 x + 3 x)%e + 5 x
[-------------------------------------,
+-------+
3| x
x\|%e + x
+-------+
3| x 2 x 2
3 \|%e + x + (2 x + 3 x)%e + 5 x
-------------------------------------]
+-------+
3| x
x\|%e + x
Type: Tuple(Expression(Integer))
fricas
)clear value t
integrate(sqrt(A-2*t*t/((1-t*t)^2))*2/(1+t*t), t)
(75)
[
+---------+
\|- 4 A - 2
*
log
+------------------------+
| 4 2
3 +---------+ |A t + (- 2 A - 2)t + A 4
(2 t - 2 t)\|- 4 A - 2 |------------------------ + A t
| 4 2
\| t - 2 t + 1
+
2
(- 6 A - 4)t + A
/
4 2
t + 2 t + 1
+
+-+
+-+ t\|2
2 \|2 atan(-----------------------------------)
+------------------------+
| 4 2
2 |A t + (- 2 A - 2)t + A
(t - 1) |------------------------
| 4 2
\| t - 2 t + 1
/
4
,
+-------+
+-------+ t\|4 A + 2
- \|4 A + 2 atan(-----------------------------------)
+------------------------+
| 4 2
2 |A t + (- 2 A - 2)t + A
(t - 1) |------------------------
| 4 2
\| t - 2 t + 1
+
+-+
+-+ t\|2
\|2 atan(-----------------------------------)
+------------------------+
| 4 2
2 |A t + (- 2 A - 2)t + A
(t - 1) |------------------------
| 4 2
\| t - 2 t + 1
/
2
]
Type: Union(List(Expression(Integer)),...)
fricas
integrate(x/sqrt(2*%pi)*exp(-1/2*log(x)^2),x=0..%plusInfinity)
2 +-+ +---+
%e \|2 \|%pi
(76) -------------
+-----+
\|2 %pi
Type: Union(f1: OrderedCompletion
?(Expression(Integer)),
...)
fricas
guess([3,6,9,12,15,18,21,24,27,30])
(77) [3 n + 3]
Type: List(Expression(Integer))
fricas
integrate(5*x^2/sqrt(x^6+x),x)
+------+
2 | 6 5
(78) log(2 x \|x + x + 2 x + 1)
Type: Union(Expression(Integer),...)
fricas
integrate(x/((x^2+1)*sqrt(x^3-x)),x)
(79)
+------+
2 | 3 4 3 2
(4 x + 8 x - 4)\|x - x + x + 8 x + 2 x - 8 x + 1
log(------------------------------------------------------)
4 2
x + 2 x + 1
+
+------+
2 | 3 4 2
(2 x - 4 x - 2)\|x - x + x - 6 x + 1
2 atan(-----------------------------------------)
+------+
2 | 3 3
(2 x + 4 x - 2)\|x - x + 4 x - 4 x
/
8
Type: Union(Expression(Integer),...)
- This surprisingly gives a real-valued elementary answer
- compared to complex one in Z&M's article!
fricas
integrate((100*e^(2*x)+100*e^(-2*x)-199)^(1/2), x)
(80)
-
600
*
weierstrassZeta
9601
----
7500
,
1074401
- -------
3375000
,
2 x log(e)
9601 1074401 300 %e - 199
weierstrassPInverse(----,- -------,----------------------)
7500 3375000 300
+
2 x log(e)
9601 1074401 300 %e - 199
- 199 weierstrassPInverse(----,- -------,----------------------)
7500 3375000 300
+
+--------------------------------------------+
| 2 x log(e) 2 2 x log(e)
|100 (%e ) - 199 %e + 100
- 30 |--------------------------------------------
| 2 x log(e)
\| %e
/
30 log(e)
Type: Union(Expression(Integer),...)
![\label{eq2}\left[{t ={\frac{-{\sqrt{{{v}^{2}}+{2 \ a \ s}}}- v}{a}}}, \:{t ={\frac{{\sqrt{{{v}^{2}}+{2 \ a \ s}}}- v}{a}}}\right]
\label{eq2}\left[{t ={\frac{-{\sqrt{{{v}^{2}}+{2 \ a \ s}}}- v}{a}}}, \:{t ={\frac{{\sqrt{{{v}^{2}}+{2 \ a \ s}}}- v}{a}}}\right]](images/7664163118707519620-16.0px.png)