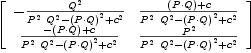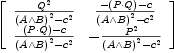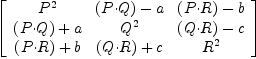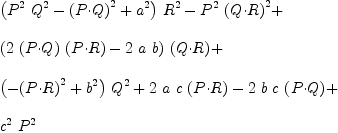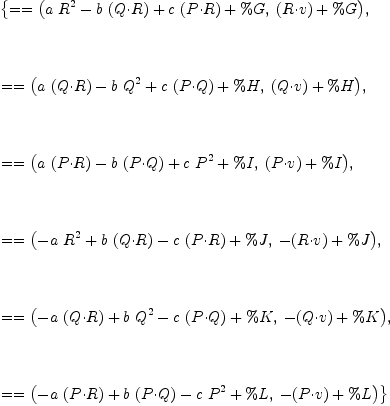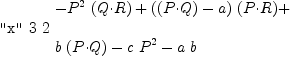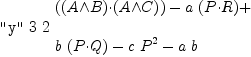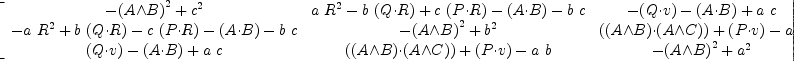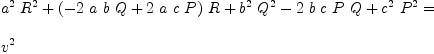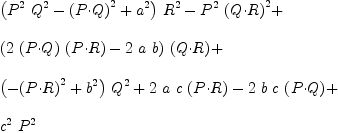Isometry from Grassmann Multivectors
Representation
K is a unital associative and commutative ring represented by polynomials
with rational coefficients of a set of symbols.
fricas
K:=SparseMultivariatePolynomial(Fraction Integer,Symbol)
Type: Type
The Grassmann Hopf K-algebra is represented by the Axiom domain Expression
consisting of rational functions with coefficients from K over an additional
set of symbols and common mathematical operators.
fricas
E:=Expression K
Type: Type
fricas
a:=a::Symbol::K; b:=b::Symbol::K; c:=c::Symbol::K;
Type: SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)
fricas
P:=P::Symbol::E; Q:=Q::Symbol::E; R:=R::Symbol::E;
Type: Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))
Grassmann Algebra Operators
Symmetric inner product
fricas
idot:=display(operator('dot,2), (x:List OutputForm):OutputForm +-> if x.1=x.2 then (x.1)^2 else paren hconcat([x.1,_{_\cdot_} ,x.2]));
fricas
Dot(A:E,B:E):E == idot(A,B)
Function declaration Dot : (Expression(SparseMultivariatePolynomial(
Fraction(Integer),Symbol)), Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol))) ->
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
) has been added to workspace.
Type: Void
fricas
dot(A:E,B:E):E ==
smaller?(A,B)=>idot(A,B)
idot(B,A)
Function declaration dot : (Expression(SparseMultivariatePolynomial(
Fraction(Integer),Symbol)), Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol))) ->
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
) has been added to workspace.
Type: Void
fricas
test(dot(P, Q)=dot(Q,P))
fricas
Compiling function dot with type (Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol)),
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
)) -> Expression(SparseMultivariatePolynomial(Fraction(Integer),
Symbol))Type: Boolean
Exterior product
fricas
ihat:=display(operator('hat,2), (x:List OutputForm):OutputForm +-> paren hconcat([x.1,_{_\wedge_} ,x.2]));
fricas
Hat(A:E,B:E):E == ihat(A,B)
Function declaration Hat : (Expression(SparseMultivariatePolynomial(
Fraction(Integer),Symbol)), Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol))) ->
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
) has been added to workspace.
Type: Void
fricas
hat(A:E,B:E):E ==
A=B=>0
smaller?(A,B)=>ihat(A,B)
-ihat(B,A)
Function declaration hat : (Expression(SparseMultivariatePolynomial(
Fraction(Integer),Symbol)), Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol))) ->
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
) has been added to workspace.
Type: Void
fricas
test(hat(P, Q)=-hat(Q,P)) and test(hat(P,P)=0)
fricas
Compiling function hat with type (Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol)),
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
)) -> Expression(SparseMultivariatePolynomial(Fraction(Integer),
Symbol))Type: Boolean
fricas
combine:=rule
Dot(-A,B) == -dot(A,B)
Dot(A,-B) == -dot(A,B)
Dot(A,B)^2-Dot(A,A)*Dot(B,B) == hat(A,B)^2
-Dot(A,B)^2+Dot(A,A)*Dot(B,B) == -hat(A,B)^2
Dot(A,B)*Dot(A,C)-Dot(A,A)*Dot(B,C) == dot(hat(A,B),hat(A,C))
Dot(A,B)*Dot(B,C)-Dot(B,B)*Dot(A,C) == dot(hat(B,A),hat(B,C))
Dot(B,C)*Dot(A,C)-Dot(C,C)*Dot(A,B) == dot(hat(C,A),hat(C,B))
fricas
Compiling function Dot with type (Expression(
SparseMultivariatePolynomial(Fraction(Integer),Symbol)),
Expression(SparseMultivariatePolynomial(Fraction(Integer),Symbol)
)) -> Expression(SparseMultivariatePolynomial(Fraction(Integer),
Symbol))Type: Ruleset(Integer,
SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol),
Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
- Isometry from Bivector
In 1937 Elie Cartan observed that the Lie algebra of the isometry group
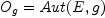 , is given by bivectors
, is given by bivectors 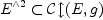 .
.
fricas
eq33 := matrix [[-dot(P,P), dot(Q,P)+c], _
[-dot(P,Q)+c, dot(Q,Q) ]]
Type: Matrix(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
eq35 := inverse(eq33)
Type: Union(Matrix(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))),
...)
fricas
map(x+->combine(x),eq35)
Type: Matrix(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
- Isometry from Trivector
Consider the following endomorphism,
fricas
eq44 := matrix [[dot(P,P), dot(Q,P)-a, dot(R,P)-b], _
[dot(P,Q)+a, dot(Q,Q), dot(R,Q)-c], _
[dot(P,R)+b, dot(Q,R)+c, dot(R,R) ]]
Type: Matrix(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
eq47a := adjoint(eq44);
Type: Record(adjMat: Matrix(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))),
detMat: Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
--)set output tex off
--)set output algebra on
eq47a.adjMat::List List E
Type: List(List(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))))
fricas
--)set output tex on
--)set output algebra off
eq47a.detMat
Type: Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))
Simplifications
fricas
eq45 := a*R-b*Q+c*P = v
Type: Equation(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
eq45a := rule
a*Dot(R,R)-b*Dot(Q,R)+c*Dot(P,R) == dot(R,v)
a*Dot(Q,R)-b*Dot(Q,Q)+c*Dot(P,Q) == dot(Q,v)
a*Dot(P,R)-b*Dot(P,Q)+c*Dot(P,P) == dot(P,v)
-a*Dot(R,R)+b*Dot(Q,R)-c*Dot(P,R) == -dot(R,v)
-a*Dot(Q,R)+b*Dot(Q,Q)-c*Dot(P,Q) == -dot(Q,v)
-a*Dot(P,R)+b*Dot(P,Q)-c*Dot(P,P) == -dot(P,v)
Type: Ruleset(Integer,
SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol),
Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
for i in 3..3 repeat
for j in 2..2 repeat
x:=(eq47a.adjMat)(i,j); outputAsTex ["x",i,j,x]
y:=combine(x); outputAsTex ["y",i,j,y]
z:=eq45a(y)
outputAsTex ["z",i,j,z]
Type: Void
fricas
eq45x := rule
-a*Dot(A,C)+b*Dot(A,B)-c*Dot(A,A) == -dot(A,v)
Type: RewriteRule
?(Integer,
SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol),
Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
z
Type: Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))
fricas
eq45x z
Type: Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))
fricas
variables(z)
Type: List(Symbol)
fricas
eq47b := map(x+-> eq45a combine(x),eq47a.adjMat)
Type: Matrix(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
map(x+->x^2,eq45)
Type: Equation(Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
eq47d := rule
Dot(R,R)*a^2 + Dot(Q,Q)*b^2 + dot(P,P)*c^2 - _
2*c*b*Dot(P,Q) + 2*a*c*Dot(P,R) - 2*a*b*Dot(Q,R) == v^2
Type: RewriteRule
?(Integer,
SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol),
Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol)))
fricas
eq47d(eq47a.detMat)
Type: Expression(SparseMultivariatePolynomial
?(Fraction(Integer),
Symbol))