This page makes test uses of the guessing package by Martin Rubey. Feel
free to add new sequences or change the sequences to ones you like to try.
See GuessingFormulasForSequences for some explanations.
fricas
(1) -> guess([1, 4, 11, 35, 98, 294, 832, 2401, 6774, 19137, 53466, 148994, 412233], [guessRat], [guessSum, guessProduct], maxLevel==2)
Type: List(Expression(Integer))
The answer being an empty list tells us, that there is no
rational function of total degree less than 13, that generates
these numbers. Furthermore, for 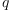 being such a rational
function, there is no formula of the form
being such a rational
function, there is no formula of the form 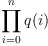 or
or
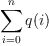 , nor
, nor 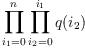 ,
nor replacing the products by sums. In fact, if you look at
Sloane's encyclopedia, you will find a good reason for that: I'd
by very surprised to find such a simple formula for such a family
of objects...
,
nor replacing the products by sums. In fact, if you look at
Sloane's encyclopedia, you will find a good reason for that: I'd
by very surprised to find such a simple formula for such a family
of objects...
fricas
guessExpRat [(1+x)^x for x in 0..3]
Type: List(Expression(Integer))
A workaround is necessary, because of bug #128
fricas
l := [1, 1, 1+q, 1+q+q^2, 1+q+q^2+q^3+q^4, 1+q+q^2+q^3+2*q^4+q^5+q^6, 1+q+q^2+q^3+2*q^4+2*q^5+2*q^6+q^7+q^8+q^9, (1+q^4+q^6)*(1+q+q^2+q^3+q^4+q^5+q^6), (1+q^4)*(1+q+q^2+q^3+q^4+q^5+2*q^6+2*q^7+2*q^8+2*q^9+q^10+q^11+q^12)]
Type: List(Polynomial(Integer))
fricas
guessPRec(q)(l, []).1
Type: Expression(Integer)
Here are some that are tried:
fricas
listA := [1,1,2,5,14,42,132];
Type: List(PositiveInteger
?)
fricas
listB := [1,2,6,21,80, 322];
Type: List(PositiveInteger
?)
fricas
listC := [1,1,2,7,42,429,7436,218348];
Type: List(PositiveInteger
?)
fricas
guess(listA, [guessRat], [guessSum, guessProduct])
Type: List(Expression(Integer))
fricas
guess(listB, [guessRat], [guessSum, guessProduct])
Type: List(Expression(Integer))
fricas
guess(listC, [guessRat], [guessProduct]).1
Type: Expression(Integer)
fricas
l := [-1/3,-11/25,-23/49,-13/27,-59/121,-83/169]
Type: List(Fraction(Integer))
fricas
guess(l, [guessRat], [guessSum, guessProduct], maxLevel==2)
Type: List(Expression(Integer))
fricas
listD := [1,1,2,6,26,162,1450,18626];
Type: List(PositiveInteger
?)
fricas
listE := [1,1,2,6,28,202,2252];
Type: List(PositiveInteger
?)
fricas
guess(listD, [guessRat], [guessProduct])
Type: List(Expression(Integer))
fricas
guess(listE, [guessRat], [guessProduct])
Type: List(Expression(Integer))
fricas
li := [-86, -975, -100, -1728, -31213];
Type: List(Integer)
fricas
guess(li, [guessRat], [guessSum, guessProduct])
Type: List(Expression(Integer))
"Most" sequences arising in combinatorics are P-recursive:
fricas
l := [1,1,6,54,660,10260,194040,4326840,111177360,3234848400,105135861600,3775206204000]
Type: List(PositiveInteger
?)
fricas
guessPRec(l).1
Type: Expression(Integer)
Power of a P-recursive sequence is again a P-recursive sequence
(we switch to text output for the next two sequences because TeX
messes the formulas):
fricas
)set output tex off
fricas
)set output algebra on
l := [hermiteH(n, 3)^4 for n in 0..110];
Type: List(Integer)
fricas
guessPRec(l, safety==10)
(22)
[
[
f(n):
3 2
(- 2 n + 75 n - 883 n + 3120)f(n + 5)
+
5 4 3 2
(8 n - 668 n + 18104 n - 207512 n + 1002128 n - 1675520)
*
f(n + 4)
+
7 6 5 4 3
64 n - 5440 n + 152048 n - 1798384 n + 7875968 n
+
2
9706784 n - 165360320 n + 326726400
*
f(n + 3)
+
9 8 7 6 5
- 256 n + 20736 n - 513216 n + 4234176 n + 5618496 n
+
4 3 2
- 183387456 n + 187255936 n + 2614783104 n - 2278264320 n
+
- 13442457600
*
f(n + 2)
+
11 10 9 8 7
- 512 n + 35072 n - 560128 n - 600320 n + 44719104 n
+
6 5 4 3
59460096 n - 1210722304 n - 3830374400 n + 5429444608 n
+
2
41504940032 n + 67395551232 n + 36498309120
*
f(n + 1)
+
13 12 11 10 9
2048 n - 29696 n - 297984 n + 2210816 n + 28607488 n
+
8 7 6 5
65614848 n - 352019456 n - 2713947136 n - 8308030464 n
+
4 3 2
- 14724902912 n - 16198819840 n - 10931650560 n
+
- 4153393152 n - 681246720
*
f(n)
=
0
,
f(0) = 1, f(1) = 1296, f(2) = 1336336, f(3) = 1049760000]
]
Type: List(Expression(Integer))
We can guess also equation for sequence of polynomials:
fricas
l := [hermiteH(n, x)^4 for n in 0..110];
Type: List(Polynomial(Integer))
fricas
guessPRec(l, safety==10)
(24)
[
[
f(n):
6 4 2 2 3 2
8 x + (- 16 n - 40)x + (10 n + 50 n + 62)x - 2 n - 15 n
+
- 37 n - 30
*
f(n + 5)
+
10 8 2 6
- 128 x + (448 n + 1408)x + (- 576 n - 3616 n - 5600)x
+
3 2 4
(336 n + 3152 n + 9696 n + 9760)x
+
4 3 2 2 5 4
(- 88 n - 1096 n - 5016 n - 9968 n - 7232)x + 8 n + 124 n
+
3 2
752 n + 2224 n + 3200 n + 1792
*
f(n + 4)
+
12 2 10
(1024 n + 4096)x + (- 4608 n - 32768 n - 57344)x
+
3 2 8
(8192 n + 83968 n + 284160 n + 317440)x
+
4 3 2 6
(- 7296 n - 97920 n - 488960 n - 1076224 n - 880640)x
+
5 4 3 2
3392 n + 56384 n + 372096 n + 1218048 n + 1976896 n
+
1272064
*
4
x
+
6 5 4 3 2
- 768 n - 15232 n - 124896 n - 541664 n - 1309792 n
+
- 1673472 n - 882176
*
2
x
+
7 6 5 4 3 2
64 n + 1472 n + 14384 n + 77360 n + 247136 n + 468608 n
+
487936 n + 215040
*
f(n + 3)
+
3 2 12
(- 4096 n - 40960 n - 135168 n - 147456)x
+
4 3 2 10
(18432 n + 237568 n + 1140736 n + 2420736 n + 1916928)x
+
5 4 3 2
- 32768 n - 516096 n - 3233792 n - 10080256 n
+
- 15636480 n - 9658368
*
8
x
+
6 5 4 3
29184 n + 542208 n + 4175360 n + 17060352 n
+
2
39012352 n + 47339520 n + 23814144
*
6
x
+
7 6 5 4
- 13568 n - 290048 n - 2642688 n - 13302528 n
+
3 2
- 39951616 n - 71583232 n - 70842624 n - 29869056
*
4
x
+
8 7 6 5 4
3072 n + 74240 n + 780160 n + 4655744 n + 17254912 n
+
3 2
40661888 n + 59489152 n + 49392384 n + 17814528
*
2
x
+
9 8 7 6 5
- 256 n - 6912 n - 82368 n - 568512 n - 2504256 n
+
4 3 2
- 7299648 n - 14077952 n - 17319168 n - 12331008 n - 3870720
*
f(n + 2)
+
6 5 4 3 2
8192 n + 131072 n + 860160 n + 2965504 n + 5668864 n
+
5701632 n + 2359296
*
10
x
+
7 6 5 4
- 28672 n - 540672 n - 4321280 n - 18980864 n
+
3 2
- 49496064 n - 76644352 n - 65273856 n - 23592960
*
8
x
+
8 7 6 5
36864 n + 800768 n + 7542784 n + 40245248 n
+
4 3 2
133052416 n + 279130112 n + 362930176 n + 267436032 n
+
85524480
*
6
x
+
9 8 7 6
- 21504 n - 529408 n - 5745664 n - 36082688 n
+
5 4 3 2
- 144510976 n - 382810112 n - 670806016 n - 749903872 n
+
- 485376000 n - 138608640
*
4
x
+
10 9 8 7
5632 n + 155136 n + 1906688 n + 13770240 n
+
6 5 4 3
64722432 n + 206893056 n + 455585792 n + 682500096 n
+
2
665804800 n + 382009344 n + 97910784
*
2
x
+
11 10 9 8 7
- 512 n - 15616 n - 214528 n - 1752320 n - 9457152 n
+
6 5 4 3
- 35414016 n - 93908992 n - 176377856 n - 229990400 n
+
2
- 198344704 n - 101842944 n - 23592960
*
f(n + 1)
+
10 9 8 7
- 8192 n - 163840 n - 1433600 n - 7225344 n
+
6 5 4 3
- 23224320 n - 49741824 n - 71901184 n - 69287936 n
+
2
- 42631168 n - 15138816 n - 2359296
*
6
x
+
11 10 9 8
16384 n + 385024 n + 4014080 n + 24485888 n
+
7 6 5 4
97026048 n + 262053888 n + 491995136 n + 641884160 n
+
3 2
570277888 n + 328695808 n + 110690304 n + 16515072
*
4
x
+
12 11 10 9
- 10240 n - 276480 n - 3350528 n - 24074240 n
+
8 7 6
- 114114560 n - 375576576 n - 879288320 n
+
5 4 3
- 1474308096 n - 1756051456 n - 1448587264 n
+
2
- 785539072 n - 251510784 n - 35979264
*
2
x
+
13 12 11 10 9
2048 n + 62464 n + 863232 n + 7150592 n + 39574528 n
+
8 7 6 5
154383360 n + 436335616 n + 903812096 n + 1370926080 n
+
4 3 2
1502906368 n + 1156861952 n + 591962112 n + 180486144 n
+
24772608
*
f(n)
=
0
,
4 8 6 4 2
f(0) = 1, f(1) = 16 x , f(2) = 256 x - 512 x + 384 x - 128 x + 16,
12 10 8 6 4
f(3) = 4096 x - 24576 x + 55296 x - 55296 x + 20736 x ]
]
Type: List(Expression(Integer))
fricas
)set output tex on
fricas
)set output algebra off
fricas
guess([1,1,2,7,40,355,4720,91690,2559980,101724390], [guessRat], [guessSum, guessProduct], maxLevel==2)
Type: List(Expression(Integer))
fricas
guess([1, 2, 3, 7, 11, 16, 26, 36, 56, 81, 131, 183, 287, 417, 677], [guessRat], [guessSum, guessProduct], maxLevel==2)
Type: List(Expression(Integer))
fricas
guess([1,1,2,7,40,355,4720,91690,2559980,101724390,5724370860,455400049575], [guessRat], [guessSum, guessProduct], maxLevel==2)
Type: List(Expression(Integer))
fricas
guess([1,1,4,35,545,13520,499215,26269200,1917388310,191268774585], [guessRat], [guessSum, guessProduct], maxLevel==2)
Type: List(Expression(Integer))
fricas
x1:=1;
fricas
x2:=8;
fricas
x3:=11;
fricas
x4:=16;
fricas
x5:=12;
fricas
x6:=16;
fricas
x7:=12;
fricas
l := [x1,x2,x3,x4,x5,x6,x7];
Type: List(PositiveInteger
?)
fricas
guessHolo(l)
Type: List(Expression(Integer))
fricas
guess(l)
Type: List(Expression(Integer))
fricas
guess(l, [guessRat], [guessSum, guessProduct], maxLevel==8)
Type: List(Expression(Integer))
fricas
guessPRec(l)
Type: List(Expression(Integer))
fricas
guessADE(l)
Type: List(Expression(Integer))
fricas
guessPRec(l)
Type: List(Expression(Integer))
fricas
guessHolo(l)
Type: List(Expression(Integer))
fricas
guessAlg(l)
Type: List(Expression(Integer))
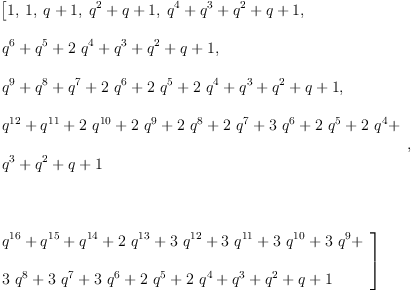
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{{f \left({n}\right)}\mbox{\rm :}}{{{q \ {f \left({n}\right)}\ {{q}^{n}}}-{f \left({n + 2}\right)}+{f \left({n + 1}\right)}}= 0}}, \:{{f \left({0}\right)}= 1}, \: \right.
\
\
\displaystyle
\left.{{f \left({1}\right)}= 1}\right]
\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{{f \left({n}\right)}\mbox{\rm :}}{{{q \ {f \left({n}\right)}\ {{q}^{n}}}-{f \left({n + 2}\right)}+{f \left({n + 1}\right)}}= 0}}, \:{{f \left({0}\right)}= 1}, \: \right.
\
\
\displaystyle
\left.{{f \left({1}\right)}= 1}\right]](images/1166922280319524024-16.0px.png)
![\label{eq5}\left[{\prod_{
\displaystyle
{{p_{7}}= 0}}^{
\displaystyle
{n - 1}}{\frac{{4 \ {p_{7}}}+ 2}{{p_{7}}+ 2}}}\right]
\label{eq5}\left[{\prod_{
\displaystyle
{{p_{7}}= 0}}^{
\displaystyle
{n - 1}}{\frac{{4 \ {p_{7}}}+ 2}{{p_{7}}+ 2}}}\right]](images/2251505039735867295-16.0px.png)
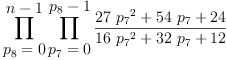
![\label{eq8}\begin{array}{@{}l}
\displaystyle
\left[ -{\frac{1}{3}}, \: -{\frac{11}{25}}, \: -{\frac{23}{49}}, \: -{\frac{13}{27}}, \: -{\frac{59}{121}}, \right.
\
\
\displaystyle
\left.\: -{\frac{83}{169}}\right]
\label{eq8}\begin{array}{@{}l}
\displaystyle
\left[ -{\frac{1}{3}}, \: -{\frac{11}{25}}, \: -{\frac{23}{49}}, \: -{\frac{13}{27}}, \: -{\frac{59}{121}}, \right.
\
\
\displaystyle
\left.\: -{\frac{83}{169}}\right]](images/4560116179250143652-16.0px.png)
![\label{eq13}\begin{array}{@{}l}
\displaystyle
\left[ 1, \: 1, \: 6, \:{54}, \:{660}, \:{10260}, \:{194040}, \:{4326840}, \:{111177360}, \: \right.
\
\
\displaystyle
\left.{3234848400}, \:{105135861600}, \:{3775206204000}\right]
\label{eq13}\begin{array}{@{}l}
\displaystyle
\left[ 1, \: 1, \: 6, \:{54}, \:{660}, \:{10260}, \:{194040}, \:{4326840}, \:{111177360}, \: \right.
\
\
\displaystyle
\left.{3234848400}, \:{105135861600}, \:{3775206204000}\right]](images/5170788584070598217-16.0px.png)
![\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{{{f \left({n}\right)}\mbox{\rm :}}{{{f \left({n + 2}\right)}+{{\left(-{4 \ n}- 6 \right)}\ {f \left({n + 1}\right)}}+{{\left({2 \ {{n}^{2}}}+{4 \ n}\right)}\ {f \left({n}\right)}}}= 0}}, \right.
\
\
\displaystyle
\left.\:{{f \left({0}\right)}= 1}, \:{{f \left({1}\right)}= 1}\right]
\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{{{f \left({n}\right)}\mbox{\rm :}}{{{f \left({n + 2}\right)}+{{\left(-{4 \ n}- 6 \right)}\ {f \left({n + 1}\right)}}+{{\left({2 \ {{n}^{2}}}+{4 \ n}\right)}\ {f \left({n}\right)}}}= 0}}, \right.
\
\
\displaystyle
\left.\:{{f \left({0}\right)}= 1}, \:{{f \left({1}\right)}= 1}\right]](images/4751471392109749243-16.0px.png)