Lorentz transformations relate one object or observer (represented by a
time-like 4-vector) to another object or observer. A Lorentz transformation
is not uniquely given by the relative velocity of these objects.
References
- Z. Oziewicz, 2005
- Special relativity without Lorentz group
- Donald Fahnline, AJP, 1982
- A covariant four-dimensional expression for Lorentz transformations
- Daniel Gottlieb, 1996
- Skew Symmetric Bundle Maps on Space-Time
Mathematical Preliminaries (from: SandBoxCategoricalRelativity)
This package implements a vector as a 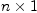 matrix (column vector),
a co-vector as a
matrix (column vector),
a co-vector as a 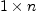 matrix (row vector), inner and outter
(tensor) products with Minkowski signature
matrix (row vector), inner and outter
(tensor) products with Minkowski signature 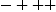 and fast routines
for checking equations.
and fast routines
for checking equations.
fricas
(1) -> <aldor>
#include "axiom.as"
#pile
-- Try RealClosure instead of AlgebraicNumber in order to
-- avoid error message #305 ... but it takes too long.
RAN ==> AlgebraicNumber
--RAN ==> RealClosure( Fraction(Integer) )
EQ ==> Equation
EXPR ==> Expression
INT ==> Integer
NNI ==> NonNegativeInteger
SYMBOL ==> Symbol
LIST ==> List
MATRIX ==> Matrix
SCALAR ==> Expression Integer
import from
INT, NNI
EXPR INT
EXPR RAN
EQ EXPR INT
LIST EXPR INT
LIST LIST SYMBOL
ListFunctions2(SCALAR, LIST SCALAR)
ListFunctions2(SYMBOL, EQ SCALAR)
ListFunctions2(SYMBOL, EQ EXPR RAN)
ListFunctions2(SCALAR, LIST SYMBOL)
ListFunctions2(EXPR RAN, LIST SYMBOL)
MATRIX SCALAR
MATRIX EXPR RAN
minkowski1(): with
+++ Colum vector
vect: LIST SCALAR -> MATRIX SCALAR
++ is represented as a nx1 matrix (column vector)
+++ The Lorentz form
g: () -> MATRIX SCALAR
g: MATRIX SCALAR -> MATRIX SCALAR
++ applied to vector produces a row vector
g: (MATRIX SCALAR,MATRIX SCALAR) -> SCALAR
++ as inner product of two vectors produces a scalar
+++ replace symbols by random numerical values.
possible: SCALAR -> SCALAR
possible: EXPR RAN -> EXPR RAN
possible: MATRIX SCALAR -> MATRIX SCALAR
possible: EQ SCALAR -> EQ SCALAR
possible: EQ MATRIX SCALAR -> EQ MATRIX SCALAR
+++ verify equality
Is?: EQ SCALAR -> Boolean
Is?: EQ EXPR RAN -> Boolean
Is?: EQ MATRIX EXPR RAN -> Boolean
+++ Massive Objects
obs: () -> MATRIX SCALAR
obs?: MATRIX SCALAR -> Boolean
+++ Relative Velocity
w: (MATRIX SCALAR,MATRIX SCALAR) -> MATRIX SCALAR
+++ outter (tensor) product
/\: (MATRIX SCALAR,MATRIX SCALAR) ->MATRIX SCALAR
+++ Lorentz factor
gamma: MATRIX SCALAR -> SCALAR
+++ binary boost
b: (MATRIX SCALAR,MATRIX SCALAR) ->MATRIX SCALAR
+++ addition of relative velocities
addition: (MATRIX SCALAR,MATRIX SCALAR,MATRIX SCALAR) -> MATRIX SCALAR
== add
--
-- Local functions
randumb(y:SYMBOL):EQ SCALAR ==
coerce(y)$SCALAR = coerce(random(100) - random(100))$SCALAR
randumb(y:SYMBOL):EQ EXPR RAN ==
coerce(y)$EXPR(RAN) = coerce(random(100) - random(100))$EXPR(RAN)
--
-- get list of unique variables
varList(x:MATRIX SCALAR):LIST Symbol ==
removeDuplicates(reduce(append,map(variables,members(x))))
varList(x:EQ MATRIX SCALAR):LIST Symbol ==
removeDuplicates(reduce(append,
append(map(variables,members(lhs x)),map(variables,members(rhs x)))
))
varList(x:EQ SCALAR):LIST Symbol ==
removeDuplicates(append(variables lhs x,variables rhs x))
--
-- Exported functions
vect(x:LIST SCALAR):MATRIX SCALAR == matrix( map(list,x) )
g():MATRIX SCALAR ==
diagonalMatrix([-1,1,1,1])$MATRIX(SCALAR)
g(x:Matrix SCALAR):MATRIX SCALAR ==
transpose(x)*g()
g(x:MATRIX SCALAR,y:MATRIX SCALAR):SCALAR ==
(g(x)*y).(1,1)
--
-- For difficult verifications it is sometimes convenient to replace
-- symbols by random numerical values.
possible(x:SCALAR):SCALAR ==
eval(x, map(randumb,variables x))
possible(x:EXPR RAN):EXPR RAN ==
eval(x, map(randumb,variables x))
possible(x:MATRIX SCALAR):MATRIX SCALAR ==
eval(x, map(randumb,varList x))
--
-- We must be careful to give each variable the same value
possible(x:EQ MATRIX SCALAR):EQ MATRIX SCALAR ==
rlist:LIST EQ SCALAR := map(randumb,varList x)
eval(lhs x, rlist) = eval(rhs x, rlist)
possible(x:EQ SCALAR):EQ SCALAR ==
rlist:List EQ SCALAR := map(randumb,varList x)
eval(lhs x, rlist) = eval(rhs x, rlist)
--
-- To verify equality, the AlgebraicNumber domain can test for
-- equality of complicated expressions involving $\sqrt{n}$.
Is?(eq:EQ SCALAR):Boolean ==
zero?(lhs(eq)-rhs(eq))
Is?(eq:EQ EXPR RAN):Boolean ==
zero?(lhs(eq)-rhs(eq))
Is?(eq:EQ Matrix EXPR RAN):Boolean ==
every?(zero?,lhs(eq)-rhs(eq))
--
-- Fast check: If the result of Is?(possible(...)) is false then the
-- equality does not hold on the other hand if it returns true, then
-- it is only probably true.
obs():MATRIX SCALAR ==
p1:=new()$SYMBOL::SCALAR;
p2:=new()$SYMBOL::SCALAR;
p3:=new()$SYMBOL::SCALAR;
vect [sqrt(p1^2::NNI+p2^2::NNI+p3^2::NNI+1),p1,p2,p3]
obs?(P:MATRIX SCALAR):Boolean ==
Is?( (g(P,P) = -1$SCALAR)$EQ(SCALAR) )
w(P:MATRIX SCALAR,Q:MATRIX SCALAR):MATRIX SCALAR ==
-Q/g(P,Q)-P
(/\)(P:MATRIX SCALAR,K:MATRIX SCALAR):MATRIX SCALAR ==
P*transpose(K) - K*transpose(P)
gamma(v:MATRIX SCALAR):SCALAR ==
1/sqrt(1-g(v,v))
b(P:MATRIX SCALAR,v:MATRIX SCALAR):MATRIX SCALAR ==
gamma(v)*(P+v)
addition(v:MATRIX SCALAR,u:MATRIX SCALAR,uinv:MATRIX SCALAR):MATRIX SCALAR ==
( u + v/gamma(u) - g(v,uinv)/g(u,u)*(u + uinv/gamma(u)) ) / (1-g(v,uinv))
++ for u=w(A,B), uinv=w(B,A) and v=w(B,C) returns w(A,C)</aldor>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/mink1.as
using Aldor compiler and options
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
Use the system command )set compiler args to change these
options.
The )library system command was not called after compilation.fricas
)lib mink1
fricas
Reading /var/aw/var/LatexWiki/mink1.asy
minkowski1 is now explicitly exposed in frame initial
minkowski1 will be automatically loaded when needed from
/var/aw/var/LatexWiki/mink1fricas
)show minkowski1
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/mink1.fasl" {1004B28523}> is
a fasl file compiled with SBCL 1.0.31, and can't be loaded into SBCL 1.1.1.
Objects
fricas
P:=obs(); Q:=obs();
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/mink1.fasl" {1004B4FB93}> is
a fasl file compiled with SBCL 1.0.31, and can't be loaded into SBCL 1.1.1.
Lorentz boost (Oziewicz)
M is a g-skew-symmetric endomorphism on the vector space
fricas
M(P,Q) == P*g(Q) - Q*g(P)
Type: Void
fricas
Is?(M(vect [a1,a2,a3,a4], vect [b1,b2,b3,b4]) = _
(vect [a1,a2,a3,a4] /\ vect [b1,b2,b3,b4])*g())
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/mink1.fasl" {10052C8DA3}> is
a fasl file compiled with SBCL 1.0.31, and can't be loaded into SBCL 1.1.1.
The Lorentz transformation is an isometry (Oziewicz):
fricas
L(b) == 1 + b + b^2/(1+sqrt(1+1/2*trace(b^2)))
Type: Void
It maps P into Q,
fricas
Is?(possible( L(M(P,Q)) * P = Q ))
There are 1 exposed and 0 unexposed library operations named g
having 1 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op g
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named g
with argument type(s)
Variable(Q)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 1 exposed and 0 unexposed library operations named g
having 1 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op g
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named g
with argument type(s)
Variable(Q)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
maps observers into observers 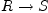
fricas
S := L(M(P,Q)) * R;
There are 1 exposed and 0 unexposed library operations named g
having 1 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op g
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named g
with argument type(s)
Variable(Q)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 1 exposed and 0 unexposed library operations named g
having 1 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op g
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named g
with argument type(s)
Variable(Q)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
and the relative velocity of w(P,Q) into minus the
inverse velocity w(Q,P)
fricas
u:=w(P,Q);
There are 1 exposed and 0 unexposed library operations named w
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op w
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named w
with argument type(s)
Variable(P)
Variable(Q)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
This Lorentz boost can be applied to other objects, for
example we can apply the boost L(M(P,Q)) to the object R to
obtain S. But in general the relative velocity w(P,Q) is not
the same as the relative velocity w(R,S)! Further since u and
v belong to separate sub-spaces, 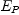 and
and 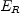 respectively,
we can not even directly compare their directions.
respectively,
we can not even directly compare their directions.
fricas
v:=w(R,S);
There are 1 exposed and 0 unexposed library operations named w
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op w
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named w
with argument type(s)
Variable(R)
Variable(S)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
The next command fails in some version of Axiom due to bug #305
fricas
Is?(possible( g(u,u) = g(v,v) ))
There are 1 exposed and 0 unexposed library operations named g
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op g
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named g
with argument type(s)
Variable(u)
Variable(u)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
The results on this page were computed with FriCAS
fricas
)version
Your user access level is compiler and this command is therefore not
available. See the )set userlevel command for more information.