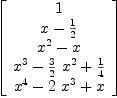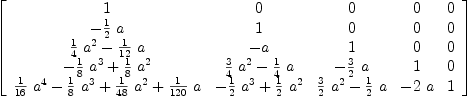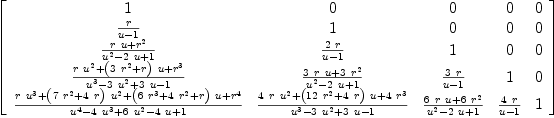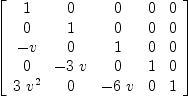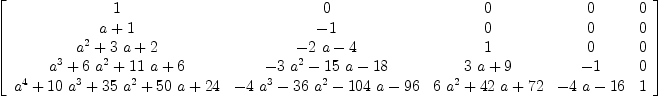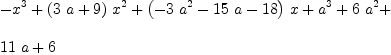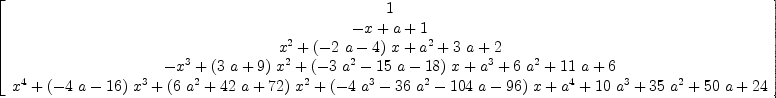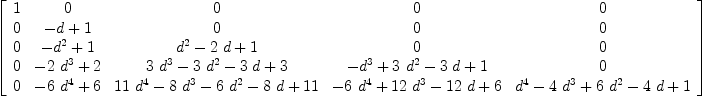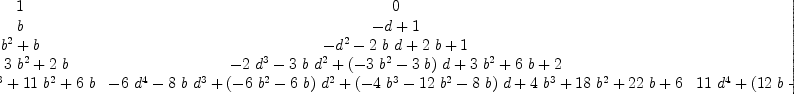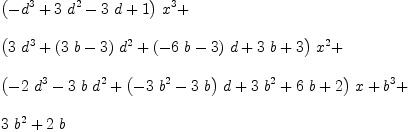fricas --- Functions to facilitate Transforming Polynomial Generating Functions into ---- Coefficient arrays. With some examples --- These are coefficient arrays (A) and can be rendered into a polynomial list --- by A*[1, Type: Void
fricas ---
---
--- Lower strict Jordan
--- When used on the left of variables x it divides by x
--- with 1/x =0
--- When used on the right of the coefficient matrix it shifts
--- the columns to the left by one.
--- Really a horizontal shift of the coefficient array and
--- Should be applied A*SJ_lower*[x...]^T
---
SJ_lower(dim) ==
J : Matrix(Polynomial(Fraction(Integer))) := new(dim,
Type: Void
fricas ---
---
--- Upper strict Jordan
--- When used on the left of variables x it multiplies by x
--- With last entry 0
--- When used on the right of coefficient matrix it shifts
--- the columns to the right by one.
---
SJ_upper(dim) ==
J : Matrix(FPFI) := new(dim,
Type: Void
fricas ---
---
--- Matrix exponential limited for now
--- Returns exp(Mat)
---
Exp_Matrix(Mat) ==
n:=nrows(Mat)
Mat_ret :Matrix(FPFI) := Mat^0
for i in 1..(n) repeat Mat_ret := Mat_ret +(Mat^i)/factorial(i)
Mat_ret
Type: Void
fricas --- --- --- Id matrix --- Exp_Matrix defined below --- Id_M(dim) == exp_tmp: Matrix(Integer) := new(dim, Type: Void
fricas --- --- --- H and Pascals matrix --- Gen_H(dim) == H : Matrix(FPFI) := new(dim, Type: Void
fricas --- --- ---Generate Pascal Matrices with a scalar (x) coefficient --- exp(x*H) --- Gen_Pascal(x, Type: Void
fricas ---
---
---H Left handed Psuedo inverse H_PIl
--- H_PIl*H ~ I
--- inverts H except for the last row.
---
Gen_H_PIl(dim) ==
H_PIl : Matrix(FPFI) := new(dim,
Type: Void
fricas --- --- --- Calculate Roman's integral equation --- (exp(x*H)-1)/H --- Which must be done in proper order --- Note that in order for the last row --- to be correct the expansion must be done --- to dim+1 and then is trimmed to dim. --- Gen_RI(x, Type: Void
fricas --- --- Type: Void
fricas --- --- (A^B) A a matrix, Type: Void
fricas ---
--- Find p in P^-1* A* P = J
--- J is really a shift
--- A must be Stricly Lower Triangular
---
ST_J(A) ==
n:=nrows(A)
m:=ncols(A)
P : Matrix(FPFI) := new(n,
Type: Void
fricas ---
--- Same as ST_H except the equation is P^-1*A *P=H
---
ST_H(A) ==
n:=nrows(A)
m:=ncols(A)
P : Matrix( FPFI) := new(n,
Type: Void
fricas --- --- --- Start of Examples --- dim:=5
Type: PositiveInteger?
fricas H:=Gen_H(dim) fricas Compiling function Gen_H with type PositiveInteger -> Matrix(
Fraction(Polynomial(Fraction(Complex(Integer)))))
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas GP :=Gen_Pascal(1, fricas Compiling function Exp_Matrix with type Matrix(Fraction(Polynomial(
Fraction(Complex(Integer))))) -> Matrix(Fraction(Polynomial(
Fraction(Complex(Integer)))))fricas Compiling function Gen_Pascal with type (PositiveInteger,
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas Id := GP^0
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- Enough is enough in taylor stream fricas )set streams calculate 4
fricas --- To change a coefficient array to the corresponding polynomial array XC := matrix[[1],
Type: Matrix(Polynomial(Integer))
fricas --- --- --- Appell Sequences --- f(t)*exp(x*t) --- --- Euler Polynmials from WikiPedia --- 2/(e^t +1) exp(x*t) --- Euler_A:=2*((GP+1)^-1)
Type: SquareMatrix?(5,
fricas --- Test Euler_A*XC
Type: Matrix(Polynomial(Fraction(Integer)))
fricas --- --- Bernoulli Polynomials from WikiPedia --- (t/(e^t -1))* exp(x*t) --- We recognize the this is Roman's integral formula --- and we have 0/0 for t/H=0 and requires special --- handling as noted above. --- Bern_Wiki_A := Gen_RI(1, fricas Compiling function Gen_H_PIl with type PositiveInteger -> Matrix(
Fraction(Polynomial(Fraction(Complex(Integer)))))fricas Compiling function Gen_RI with type (PositiveInteger,
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- --- Bernoulli of order a from Roman ------ (t/(e^t -1))^a * exp(x*t) ---- This is the same as above exponenitated --- Bern_Roman_A := Exp_Matrix_AB(Bern_Wiki_A, fricas Compiling function Ln_Uni_Matrix with type Matrix(Fraction(
Polynomial(Fraction(Complex(Integer))))) -> Matrix(Fraction(
Polynomial(Fraction(Complex(Integer)))))fricas Compiling function Exp_Matrix_AB with type (Matrix(Fraction(
Polynomial(Fraction(Complex(Integer))))),
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- ---- ---- From ----Some Identities for Euler and Bernoulli Polynomials ----and Their Zeros ---equation 4. --- by ----Taekyun Kim and Cheon Seoung Ryoo ----Frobenius–Euler polynomials of order r ---------- (1-u)/(e^t -u))^r * exp(x*t) ---- Frob_Euler_term:=((1-u)*Id_M(dim))*((Gen_Pascal(1, fricas Compiling function Exp_Matrix with type Matrix(Integer) -> Matrix(
Fraction(Polynomial(Fraction(Complex(Integer)))))fricas Compiling function Id_M with type PositiveInteger -> Matrix(Fraction
(Polynomial(Fraction(Complex(Integer)))))Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas Frob_Euler:=Exp_Matrix_AB(Frob_Euler_term, fricas Compiling function Exp_Matrix_AB with type (Matrix(Fraction(
Polynomial(Fraction(Complex(Integer))))),
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- --- --- Hermite Polynomials wiki version --- Probabilistic version ---exp(-(t^2)/2) *exp(x*t) --- Herm_Wiki_A := Exp_Matrix(-H^2/2)
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- Roman's version Herm_Roman_A := Exp_Matrix(-v*H^2/2)
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- Hermite/Gould Hopper of order 3 --- exp(y*t^3)*exp(x*t) HGH_A := Exp_Matrix(y*H^3)
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- --- --- Associated Sequences requires Jordan transform --- exp(x*f(t)) -> SJ_H(f(H)) --- --- Lower Factorial Exponential --- Roman PP 57 --- exp(x*Ln(t+1)) --- Lower_Fact_Exp_A := ST_H(Ln_Uni_Matrix(H+1)) fricas Compiling function Ln_Uni_Matrix with type SquareMatrix(5, fricas Compiling function ST_H with type Matrix(Fraction(Polynomial(
Fraction(Complex(Integer))))) -> Matrix(Fraction(Polynomial(
Fraction(Complex(Integer)))))
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- Just to verify x:='x; Type: Variable(x)
fricas 1
Type: PositiveInteger?
fricas x
Type: Variable(x)
fricas x*(x-1)
Type: Polynomial(Integer)
fricas x*(x-1)*(x-2)
Type: Polynomial(Integer)
fricas x*(x-1)*(x-2)*(x-3)
Type: Polynomial(Integer)
fricas --- --- Exponential Polynomials --- Roman PP 64 --- Also http://mathworld.wolfram.com/BellPolynomial.html --- exp(x*(exp(t)-1)) --- Exp_A := ST_H(GP-1) fricas Compiling function ST_H with type SquareMatrix(5,
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- --- -
Type: Variable(-)
fricas --- Scheffer Sequences require Jordan form --- --- g(t)*exp(x*f(t)) ->g(H)*ST_H(f(H)) --- --- Laguerre Polynomials Roman PP 110 --- (1-t)^(-a-1)*exp(x*(t/(t-1))) Lag_A := Exp_Matrix_AB(1-H, fricas Compiling function Exp_Matrix_AB with type (SquareMatrix(5,
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- Checking Lag_S:=(1-t)^(-a-1)*exp(x*(t/(t-1))); fricas Lag_S_C3:=6*coefficient(Lag_S,
Type: Expression(Integer)
fricas Lag_P:=Lag_A*XC
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas Lag_P(4,
Type: Expression(Complex(Integer))
fricas --- Note the "series" give "Power Series" to get the --- Taylor series one has to multiply by factorial(n) ---
fricas Meix_Series_R :=((1-t*d)*((1-t)^-1))^x*(1-t)^(-b)
fricas --- and the Sheffer form --- We need the Jordan form of Ln_Uni_Matrix((1-H*d)*(1-H)^-1) Meix_A_fJ := ST_H(Ln_Uni_Matrix((1-H*d)*(1-H)^-1)) fricas Compiling function Ln_Uni_Matrix with type SquareMatrix(5,
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas Meix_A := Exp_Matrix_AB(1-H,
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas --- --- Let's check Meix_C3:=6*coefficient(Meix_Series_R,
Type: Expression(Integer)
fricas Meix_P:=Meix_A*XC
Type: Matrix(Fraction(Polynomial(Fraction(Complex(Integer)))))
fricas Meix_P(4,
Type: Expression(Complex(Integer))
|
|
|
|
last edited 5 years ago by rrogers |