From: input/repa6.input
fricas
(1) -> -- This file demonstrates Representation Theory in Scratchpad
-- using the packages REP1, REP2, IRSN and SGCF, which are the
-- abbreviations for RepresentationPackage1, RepresentationPackage2
-- IrrRepSymNatPackage and SymmetricGroupCombinatoricFunctions.
-- authors: Holger Gollan, Johannes Grabmeier
-- release 1.0 09/30/87
-- release 2.0 11/10/88: J. Grabmeier: add functions from IRSN
-- release 2.1 08/04/89: J. Grabmeier: adjusting to new PERM
-- and modified REP1
-- release 2.2 06/05/89: J. Grabmeier: adjusting to new algebra
-- release 2.3 08/20/89: J. Grabmeier: minor adjustments
-- In the sequel we show how to get all 2-modular irreducible
-- representations of the alternating group A6.
-- We generate A6 by the permutations threecycle x=(1,2,3)
-- and the 5-cycle y=(2,3,4,5,6)
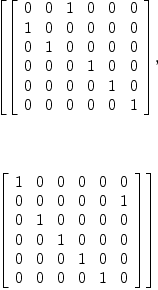
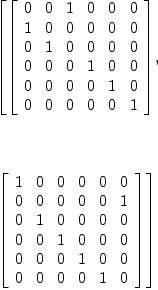
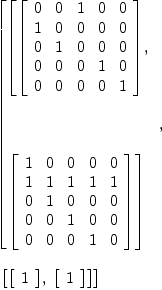
genA6 : List PERM INT := [cycle [1,2,3], cycle [2,3,4,5,6]]
Type: List(Permutation(Integer))
fricas
-- pRA6 is the permutation representation over the Integers...
pRA6 := permutationRepresentation (genA6, 6)
Type: List(Matrix(Integer))
fricas
-- ... and pRA6m2 is the permutation representation over PrimeField 2:
pRA6m2 : List Matrix PrimeField 2 := pRA6
Type: List(Matrix(PrimeField
?(2)))
fricas
-- Now try to split pRA6m2:
sp0 := meatAxe pRA6m2
Fingerprint element in generated algebra is singular
A proper cyclic submodule is found.
Transition matrix computed
The inverse of the transition matrix computed
Now transform the matrices
Type: List(List(Matrix(PrimeField
?(2))))
fricas
-- We have found the trivial module as a factormodule
-- and a 5-dimensional submodule.
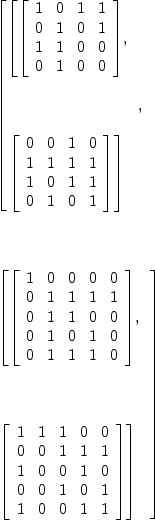
dA6d1 := sp0.2
Type: List(Matrix(PrimeField
?(2)))
fricas
-- Try to split again...
sp1 := meatAxe sp0.1
Fingerprint element in generated algebra is singular
The generated cyclic submodule was not proper
The generated cyclic submodule was not proper
The generated cyclic submodule was not proper
We know that all the cyclic submodules generated by all
non-trivial element of the singular matrix under view are
not proper, hence Norton's irreducibility test can be done:
A proper cyclic submodule is found.
Transition matrix computed
The inverse of the transition matrix computed
Now transform the matrices
Representation is not irreducible and it will be split:
Type: List(List(Matrix(PrimeField
?(2))))
fricas
-- ... and find a 4-dimensional submodule, say dA6d4a, and the
-- trivial one again.
dA6d4a := sp1.2
Type: List(Matrix(PrimeField
?(2)))
fricas
-- Now we want to test, whether dA6d4a is absolutely irreducible...
isAbsolutelyIrreducible? dA6d4a
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra has
one-dimensional kernel
We know that all the cyclic submodules generated by all
non-trivial element of the singular matrix under view are
not proper, hence Norton's irreducibility test can be done:
The generated cyclic submodule was not proper
Representation is absolutely irreducible
Type: Boolean
fricas
-- ...and see: dA6d4a is absolutely irreducible.
-- So we have found a second irreducible representation.
-- Now construct a representation from reducing an irreducible one
-- of the symmetric group S_6 over the integers taken mod 2
-- What is the degree of the representation belonging to partition
-- [2,2,1,1]?
-- lambda : PRTITION := partition [2,2,1,1]
lambda := [2,2,1,1]
Type: List(PositiveInteger
?)
fricas
dimensionOfIrreducibleRepresentation lambda
fricas
-- now create the restriction to A6:
d2211 := irreducibleRepresentation(lambda, genA6)
Type: List(Matrix(Integer))
fricas
-- ... and d2211m2 is the representation over PrimeField 2:
d2211m2 : List Matrix PrimeField 2 := d2211
Type: List(Matrix(PrimeField
?(2)))
fricas
-- and split it:
-- )set output tex off
-- )set output algebra on
sp2 := meatAxe d2211m2
Fingerprint element in generated algebra is singular
A proper cyclic submodule is found.
Transition matrix computed
The inverse of the transition matrix computed
Now transform the matrices
Type: List(List(Matrix(PrimeField
?(2))))
fricas
-- A 5 and a 4-dimensional one.
-- we take the 4-dimensional one, say dA6d4b:
dA6d4b := sp2.1
Type: List(Matrix(PrimeField
?(2)))
fricas
-- This is absolutely irreducible, too ...
isAbsolutelyIrreducible? dA6d4b
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra has
one-dimensional kernel
We know that all the cyclic submodules generated by all
non-trivial element of the singular matrix under view are
not proper, hence Norton's irreducibility test can be done:
The generated cyclic submodule was not proper
Representation is absolutely irreducible
Type: Boolean
fricas
-- ... and dA6d4a and dA6d4b are not equivalent:
areEquivalent? ( dA6d4a , dA6d4b )
Dimensions of kernels differ
Representations are not equivalent.
Type: Matrix(PrimeField
?(2))
fricas
-- So the third irreducible representation is found.
-- Now construct a new representation with the help of the tensorproduct
fricas
)set output tex off
fricas
)set output algebra on
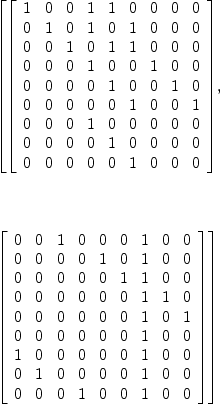
dA6d16 := tensorProduct ( dA6d4a , dA6d4b )
(17)
+0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0+
| |
|0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0|
[| |,
|1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0|
| |
+0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0+
+0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0+
| |
|0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1|
| |
|0 0 0 0 1 0 1 1 1 0 1 1 1 0 1 1|
| |
|0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1|
| |
|0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0|
| |
|1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1|
| |
|1 0 1 1 1 0 1 1 0 0 0 0 1 0 1 1|
| |
|0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1|
| |]
|0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0|
| |
|1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0|
| |
|1 0 1 1 1 0 1 1 1 0 1 1 0 0 0 0|
| |
|0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0|
| |
|0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0|
| |
|1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1|
| |
|1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1|
| |
+0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1+
Type: List(Matrix(PrimeField
?(2)))
fricas
-- and try to split it...
sp3 := meatAxe dA6d16
Fingerprint element in generated algebra is non-singular
The generated cyclic submodule was not proper
All factors were bad
Fingerprint element in generated algebra is non-singular
The generated cyclic submodule was not proper
Found good factor
We know that all the cyclic submodules generated by all
non-trivial element of the singular matrix under view are
not proper, hence Norton's irreducibility test can be done:
The generated cyclic submodule was not proper
Representation is irreducible, but we don't know
whether it is absolutely irreducible
(18)
[
+0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0+
| |
|0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0|
| |
|1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
[| |,
|0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0|
| |
+0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0+
+0 0 0 0 0 1 1 0 0 1 1 0 0 1 1 0+
| |
|0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1|
| |
|0 0 0 0 1 1 1 0 1 1 1 0 1 1 1 0|
| |
|0 0 0 0 0 1 1 1 0 1 1 1 0 1 1 1|
| |
|0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0|
| |
|0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1|
| |
|1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0|
| |
|0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1|
| |]
|0 1 1 0 0 0 0 0 0 1 1 0 0 1 1 0|
| |
|0 1 0 1 0 0 0 0 0 1 0 1 0 1 0 1|
| |
|1 1 1 0 0 0 0 0 1 1 1 0 1 1 1 0|
| |
|0 1 1 1 0 0 0 0 0 1 1 1 0 1 1 1|
| |
|0 1 1 0 0 1 1 0 0 0 0 0 0 1 1 0|
| |
|0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1|
| |
|1 1 1 0 1 1 1 0 0 0 0 0 1 1 1 0|
| |
+0 1 1 1 0 1 1 1 0 0 0 0 0 1 1 1+
]
Type: List(List(Matrix(PrimeField
?(2))))
fricas
-- The representation is irreducible, but may be not
-- absolutely irreducible.
isAbsolutelyIrreducible? dA6d16
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
We have not found a one-dimensional kernel so far,
as we do a random search you could try again
(19) false
Type: Boolean
fricas
-- So let's try the same over the field with 4 elements:
gf4 := FiniteField(2,2)
(20) FiniteField(2,2)
Type: Type
fricas
dA6d16gf4 : List Matrix gf4 := dA6d16
(21)
+0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0+
| |
|0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0|
[| |,
|1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0|
| |
+0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0+
+0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0+
| |
|0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1|
| |
|0 0 0 0 1 0 1 1 1 0 1 1 1 0 1 1|
| |
|0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1|
| |
|0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0|
| |
|1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1|
| |
|1 0 1 1 1 0 1 1 0 0 0 0 1 0 1 1|
| |
|0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1|
| |]
|0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0|
| |
|1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0|
| |
|1 0 1 1 1 0 1 1 1 0 1 1 0 0 0 0|
| |
|0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0|
| |
|0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0|
| |
|1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1|
| |
|1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1|
| |
+0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1+
Type: List(Matrix(FiniteField
?(2,
2)))
fricas
sp4 := meatAxe dA6d16gf4
The generated cyclic submodule was not proper
A proper cyclic submodule is found.
Transition matrix computed
The inverse of the transition matrix computed
Now transform the matrices
(22)
[
+%A + 1 %A 0 %A + 1 1 %A 0 0 +
| |
| 0 0 %A + 1 %A %A + 1 %A + 1 0 0 |
| |
|%A + 1 %A %A + 1 1 %A 0 0 0 |
| |
|%A + 1 %A %A + 1 1 %A + 1 0 0 0 |
[| |,
| %A 1 1 1 0 0 %A %A + 1|
| |
| 0 0 %A 1 0 0 %A + 1 0 |
| |
| 1 0 1 1 0 0 0 0 |
| |
+ 1 1 0 0 0 0 0 0 +
+ 1 0 %A + 1 0 1 1 %A + 1 %A +
| |
| 1 %A 0 0 0 %A 1 %A |
| |
|%A + 1 1 %A %A %A 1 %A + 1 0 |
| |
| %A %A 0 0 1 %A 1 1 |
| |]
| 1 0 %A 0 1 1 %A + 1 %A + 1|
| |
| 0 0 %A %A %A 1 1 %A + 1|
| |
| 0 0 1 0 0 1 0 1 |
| |
+ 0 %A + 1 0 %A + 1 1 %A %A %A + 1+
,
+ 0 1 1 %A 0 0 0 0+
| |
| 1 1 %A 0 0 0 0 0|
| |
|%A + 1 0 0 0 0 0 0 0|
| |
| 1 %A + 1 0 0 0 0 0 0|
[| |,
|%A + 1 %A 1 1 1 0 1 1|
| |
| 0 0 %A + 1 1 0 1 0 1|
| |
|%A + 1 1 0 1 1 1 0 0|
| |
+ 1 %A + 1 %A %A + 1 0 1 0 0+
+ %A 1 %A + 1 0 0 %A 0 1 +
| |
| 0 %A + 1 1 1 1 0 %A %A + 1|
| |
| 0 %A 0 %A %A 1 %A %A + 1|
| |
| 1 %A 1 %A 0 0 %A 1 |
| |]
| 0 %A + 1 0 %A %A 0 0 %A |
| |
| %A 0 %A %A + 1 0 %A 0 %A |
| |
| 0 1 0 1 %A 0 %A %A |
| |
+%A + 1 %A + 1 %A + 1 1 %A + 1 %A + 1 1 %A +
]
Type: List(List(Matrix(FiniteField
?(2,
2))))
fricas
-- Now we find two 8-dimensional ones, dA6d8a and dA6d8b.
dA6d8a : List Matrix gf4 := sp4.1
(23)
+%A + 1 %A 0 %A + 1 1 %A 0 0 +
| |
| 0 0 %A + 1 %A %A + 1 %A + 1 0 0 |
| |
|%A + 1 %A %A + 1 1 %A 0 0 0 |
| |
|%A + 1 %A %A + 1 1 %A + 1 0 0 0 |
[| |,
| %A 1 1 1 0 0 %A %A + 1|
| |
| 0 0 %A 1 0 0 %A + 1 0 |
| |
| 1 0 1 1 0 0 0 0 |
| |
+ 1 1 0 0 0 0 0 0 +
+ 1 0 %A + 1 0 1 1 %A + 1 %A +
| |
| 1 %A 0 0 0 %A 1 %A |
| |
|%A + 1 1 %A %A %A 1 %A + 1 0 |
| |
| %A %A 0 0 1 %A 1 1 |
| |]
| 1 0 %A 0 1 1 %A + 1 %A + 1|
| |
| 0 0 %A %A %A 1 1 %A + 1|
| |
| 0 0 1 0 0 1 0 1 |
| |
+ 0 %A + 1 0 %A + 1 1 %A %A %A + 1+
Type: List(Matrix(FiniteField
?(2,
2)))
fricas
dA6d8b : List Matrix gf4 := sp4.2
(24)
+ 0 1 1 %A 0 0 0 0+
| |
| 1 1 %A 0 0 0 0 0|
| |
|%A + 1 0 0 0 0 0 0 0|
| |
| 1 %A + 1 0 0 0 0 0 0|
[| |,
|%A + 1 %A 1 1 1 0 1 1|
| |
| 0 0 %A + 1 1 0 1 0 1|
| |
|%A + 1 1 0 1 1 1 0 0|
| |
+ 1 %A + 1 %A %A + 1 0 1 0 0+
+ %A 1 %A + 1 0 0 %A 0 1 +
| |
| 0 %A + 1 1 1 1 0 %A %A + 1|
| |
| 0 %A 0 %A %A 1 %A %A + 1|
| |
| 1 %A 1 %A 0 0 %A 1 |
| |]
| 0 %A + 1 0 %A %A 0 0 %A |
| |
| %A 0 %A %A + 1 0 %A 0 %A |
| |
| 0 1 0 1 %A 0 %A %A |
| |
+%A + 1 %A + 1 %A + 1 1 %A + 1 %A + 1 1 %A +
Type: List(Matrix(FiniteField
?(2,
2)))
fricas
-- Both are absolutely irreducible...
isAbsolutelyIrreducible? dA6d8a
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra has
one-dimensional kernel
We know that all the cyclic submodules generated by all
non-trivial element of the singular matrix under view are
not proper, hence Norton's irreducibility test can be done:
The generated cyclic submodule was not proper
Representation is absolutely irreducible
(25) true
Type: Boolean
fricas
isAbsolutelyIrreducible? dA6d8b
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra has
one-dimensional kernel
We know that all the cyclic submodules generated by all
non-trivial element of the singular matrix under view are
not proper, hence Norton's irreducibility test can be done:
The generated cyclic submodule was not proper
Representation is absolutely irreducible
(26) true
Type: Boolean
fricas
-- and they are not equivalent...
areEquivalent? ( dA6d8a, dA6d8b )
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra does
not have a one-dimensional kernel
Random element in generated algebra has
one-dimensional kernel
There is no isomorphism, as the only possible one
fails to do the necessary base change
Representations are not equivalent.
(27) [0]
Type: Matrix(FiniteField
?(2,
2))
fricas
-- So we have found five absolutely irreducible representations of A6
-- in characteristic 2.
-- The theory tells us that there are no more irreducible ones.
-- Here again are all absolutely irreducible 2-modular
-- representations of A6
dA6d1
(28) [[1], [1]]
Type: List(Matrix(PrimeField
?(2)))
fricas
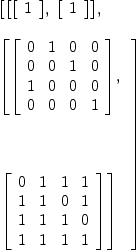
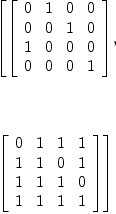
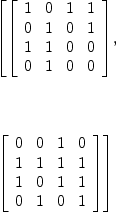
dA6d4a
+0 1 0 0+ +0 1 1 1+
| | | |
|0 0 1 0| |1 1 0 1|
(29) [| |, | |]
|1 0 0 0| |1 1 1 0|
| | | |
+0 0 0 1+ +1 1 1 1+
Type: List(Matrix(PrimeField
?(2)))
fricas
dA6d4b
+1 0 1 1+ +0 0 1 0+
| | | |
|0 1 0 1| |1 1 1 1|
(30) [| |, | |]
|1 1 0 0| |1 0 1 1|
| | | |
+0 1 0 0+ +0 1 0 1+
Type: List(Matrix(PrimeField
?(2)))
fricas
dA6d8a
(31)
+%A + 1 %A 0 %A + 1 1 %A 0 0 +
| |
| 0 0 %A + 1 %A %A + 1 %A + 1 0 0 |
| |
|%A + 1 %A %A + 1 1 %A 0 0 0 |
| |
|%A + 1 %A %A + 1 1 %A + 1 0 0 0 |
[| |,
| %A 1 1 1 0 0 %A %A + 1|
| |
| 0 0 %A 1 0 0 %A + 1 0 |
| |
| 1 0 1 1 0 0 0 0 |
| |
+ 1 1 0 0 0 0 0 0 +
+ 1 0 %A + 1 0 1 1 %A + 1 %A +
| |
| 1 %A 0 0 0 %A 1 %A |
| |
|%A + 1 1 %A %A %A 1 %A + 1 0 |
| |
| %A %A 0 0 1 %A 1 1 |
| |]
| 1 0 %A 0 1 1 %A + 1 %A + 1|
| |
| 0 0 %A %A %A 1 1 %A + 1|
| |
| 0 0 1 0 0 1 0 1 |
| |
+ 0 %A + 1 0 %A + 1 1 %A %A %A + 1+
Type: List(Matrix(FiniteField
?(2,
2)))
fricas
dA6d8b
(32)
+ 0 1 1 %A 0 0 0 0+
| |
| 1 1 %A 0 0 0 0 0|
| |
|%A + 1 0 0 0 0 0 0 0|
| |
| 1 %A + 1 0 0 0 0 0 0|
[| |,
|%A + 1 %A 1 1 1 0 1 1|
| |
| 0 0 %A + 1 1 0 1 0 1|
| |
|%A + 1 1 0 1 1 1 0 0|
| |
+ 1 %A + 1 %A %A + 1 0 1 0 0+
+ %A 1 %A + 1 0 0 %A 0 1 +
| |
| 0 %A + 1 1 1 1 0 %A %A + 1|
| |
| 0 %A 0 %A %A 1 %A %A + 1|
| |
| 1 %A 1 %A 0 0 %A 1 |
| |]
| 0 %A + 1 0 %A %A 0 0 %A |
| |
| %A 0 %A %A + 1 0 %A 0 %A |
| |
| 0 1 0 1 %A 0 %A %A |
| |
+%A + 1 %A + 1 %A + 1 1 %A + 1 %A + 1 1 %A +
Type: List(Matrix(FiniteField
?(2,
2)))
fricas
-- And here again is the irreducible, but not absolutely irreducible
-- representations of A6 over PrimeField 2
dA6d16
(33)
+0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0+
| |
|0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0|
[| |,
|1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1|
| |
|0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0|
| |
+0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0+
+0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0+
| |
|0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1|
| |
|0 0 0 0 1 0 1 1 1 0 1 1 1 0 1 1|
| |
|0 0 0 0 0 1 0 1 0 1 0 1 0 1 0 1|
| |
|0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0|
| |
|1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1|
| |
|1 0 1 1 1 0 1 1 0 0 0 0 1 0 1 1|
| |
|0 1 0 1 0 1 0 1 0 0 0 0 0 1 0 1|
| |]
|0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0|
| |
|1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0|
| |
|1 0 1 1 1 0 1 1 1 0 1 1 0 0 0 0|
| |
|0 1 0 1 0 1 0 1 0 1 0 1 0 0 0 0|
| |
|0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0|
| |
|1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1|
| |
|1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1|
| |
+0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1+
Type: List(Matrix(PrimeField
?(2)))
![\label{eq1}\left[{\left(1 \ 2 \ 3 \right)}, \:{\left(2 \ 3 \ 4 \ 5 \ 6 \right)}\right]](images/6538579023899797709-16.0px.png "\label{eq1}\left[{\left(1 \ 2 \ 3 \right)}, \:{\left(2 \ 3 \ 4 \ 5 \ 6 \right)}\right]")
![\label{eq2}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccccc}
0 & 0 & 1 & 0 & 0 & 0
\
1 & 0 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 0 & 1](images/8902783786457476208-16.0px.png "\label{eq2}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccccc}
0 & 0 & 1 & 0 & 0 & 0
\
1 & 0 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 0 & 1")
![\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccccc}
0 & 0 & 1 & 0 & 0 & 0
\
1 & 0 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 0 & 1](images/185312252635876669-16.0px.png "\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccccc}
0 & 0 & 1 & 0 & 0 & 0
\
1 & 0 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 0 & 1")
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{ccccc}
0 & 0 & 1 & 0 & 0
\
1 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 1](images/624752677013064708-16.0px.png "\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{ccccc}
0 & 0 & 1 & 0 & 0
\
1 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 1")
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccc}
0 & 1 & 0 & 0
\
0 & 0 & 1 & 0
\
1 & 0 & 0 & 0
\
0 & 0 & 0 & 1](images/5939571584534450992-16.0px.png "\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccc}
0 & 1 & 0 & 0
\
0 & 0 & 1 & 0
\
1 & 0 & 0 & 0
\
0 & 0 & 0 & 1")
![\label{eq9}\left[ 2, \: 2, \: 1, \: 1 \right]](images/4764618149747307704-16.0px.png "\label{eq9}\left[ 2, \: 2, \: 1, \: 1 \right]")
![\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{ccccccccc}
1 & 0 & 0 & - 1 & 1 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0
\
0 & 0 & 1 & 0 & 1 & - 1 & 0 & 0 & 0
\
0 & 0 & 0 & - 1 & 0 & 0 & - 1 & 0 & 0
\
0 & 0 & 0 & 0 & - 1 & 0 & 0 & - 1 & 0
\
0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 & - 1
\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0](images/1029909405755162323-16.0px.png "\label{eq11}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{ccccccccc}
1 & 0 & 0 & - 1 & 1 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0
\
0 & 0 & 1 & 0 & 1 & - 1 & 0 & 0 & 0
\
0 & 0 & 0 & - 1 & 0 & 0 & - 1 & 0 & 0
\
0 & 0 & 0 & 0 & - 1 & 0 & 0 & - 1 & 0
\
0 & 0 & 0 & 0 & 0 & - 1 & 0 & 0 & - 1
\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0")
![\label{eq12}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{ccccccccc}
1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0
\
0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1
\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0](images/6671173501161389993-16.0px.png "\label{eq12}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{ccccccccc}
1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0
\
0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 & 0
\
0 & 0 & 1 & 0 & 1 & 1 & 0 & 0 & 0
\
0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0
\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1
\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0
\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0")
![\label{eq13}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccc}
1 & 0 & 1 & 1
\
0 & 1 & 0 & 1
\
1 & 1 & 0 & 0
\
0 & 1 & 0 & 0](images/8379557691122537794-16.0px.png "\label{eq13}\begin{array}{@{}l}
\displaystyle
\left[{
\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccc}
1 & 0 & 1 & 1
\
0 & 1 & 0 & 1
\
1 & 1 & 0 & 0
\
0 & 1 & 0 & 0")
![\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccc}
1 & 0 & 1 & 1
\
0 & 1 & 0 & 1
\
1 & 1 & 0 & 0
\
0 & 1 & 0 & 0](images/2339325479697839404-16.0px.png "\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cccc}
1 & 0 & 1 & 1
\
0 & 1 & 0 & 1
\
1 & 1 & 0 & 0
\
0 & 1 & 0 & 0")
