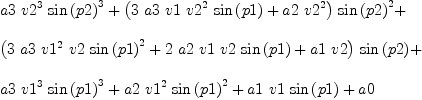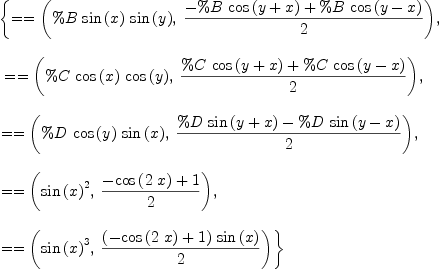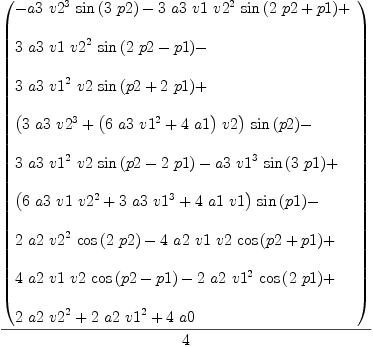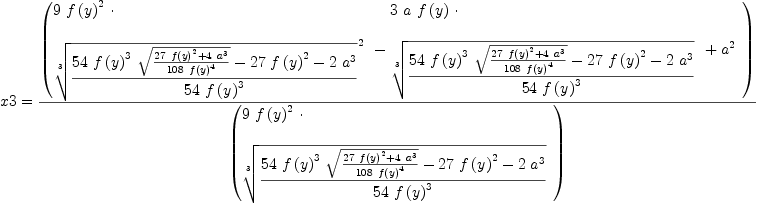Sin and Cos Rules fricas x:=v1*sin(p1)+v2*sin(p2)
Type: Expression(Integer)
fricas y:= a0 + a1*x + a2*x^2 + a3*x^3
Type: Expression(Integer)
fricas sinCosProducts := rule sin(x)*sin(y) == (cos(x-y) - cos(x+y))/2 cos(x)*cos(y) == (cos(x-y) + cos(x+y))/2 sin(x)*cos(y) == (sin(x-y) + sin(x+y))/2 sin(x)^2 == (1 - cos(2*x))/2 sin(x)^3 == sin(x)*(1 - cos(2*x))/2
Type: Ruleset(Integer,
fricas sinCosProducts(y)
Type: Expression(Integer)
Integration fricas )clear completely
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(integrate(x+y,
Type: Polynomial(Fraction(Integer))
fricas integrate(exp(-b*h*sin(o))*sin(o),
Type: Union(fail: failed,
Gosper's algorithm is implemented in Axiom fricas p:Polynomial Integer:=1+x+x^2
Type: Polynomial(Integer)
fricas sum(p,
Type: Fraction(Polynomial(Integer))
fricas e:=binomial(2*k,
Type: Expression(Integer)
fricas sum(e,
Type: Expression(Integer)
fricas sum(%,
Type: Expression(Integer)
fricas factor(4*n^2+8*n+3)
Type: Factored(Polynomial(Integer))
Examples from Petkovsek, Wilf, Zeilberger
Symbols, kernels, variables, expressions ... difficult to understand fricas e0:Expression Integer:=1+2*x^2+x
Type: Expression(Integer)
fricas kernels(e0)
Type: List(Kernel(Expression(Integer)))
fricas p0:=e0::(Polynomial Integer)
Type: Polynomial(Integer)
fricas variables(p0)
Type: List(Symbol)
fricas e1:Expression Integer:=x*sin(t)/cos(t)+1
Type: Expression(Integer)
fricas kernels(e1)
Type: List(Kernel(Expression(Integer)))
fricas solve(e1=0,
Type: List(Equation(Expression(Integer)))
fricas e2:UP(x,
Type: UnivariatePolynomial(x,
Expressions and substitution fricas f:=operator 'f; e:=1+a*x^2+f(y)*x^3; eq:=[f(y)=r]; peq:=subst(e, Type: List(Equation(Expression(Integer)))
fricas --[(lhs(s)=subst(rhs(s),
Type: Equation(Expression(Integer))
Parsing expressions ??? fricas e:Expression Integer:=x*y
Type: Expression(Integer)
fricas isMult(e)
Type: Union("failed",
fricas e1:Expression Integer:=x
Type: Expression(Integer)
fricas isMult(e1)
Type: Union(Record(coef: Integer,
fricas isMult(e1*e)
Type: Union("failed",
|
|
|
|
last edited 10 years ago by test1 |