|
fricas R ==> EXPR INT
Type: Void
fricas e:=[subscript('e, [k]) for k in 1..3]
Type: List(Symbol)
fricas g:=[subscript('g, [k]) for k in 1..4]
Type: List(Symbol)
fricas h:=[superscript('h, [k]) for k in 1..4]
Type: List(Symbol)
fricas B1:=OrderedVariableList e
Type: Type
fricas B2:=OrderedVariableList g
Type: Type
fricas B3:=OrderedVariableList h
Type: Type
fricas M1:=FreeModule(R,B1)
Type: Type
fricas M2:=FreeModule(R,B2)
Type: Type
fricas M3:=FreeModule(R,B3)
Type: Type
fricas M12:=TensorProduct(R,B1,B2,M1,M2)
Type: Type
fricas M23:=TensorProduct(R,B2,B3,M2,M3)
Type: Type
fricas M123:=TensorProduct(R,Product(B1,B2),B3,M12,M3)
Type: Type
fricas v1:=x*(e.1)::M1 - y*(e.3)::M1
fricas v2:=q*(g.2)::M2 + r*(g.4)::M2
fricas v3:=3*(h.1)::M3 - z*(h.3)::M3
fricas t12:=tensor(v1,v2)$M12
Type: TensorProduct ?(Expression(Integer), OrderedVariableList([e[1], e[2], e[3]]), OrderedVariableList([g[1], g[2], g[3], g[4]]), FreeModule(Expression(Integer), OrderedVariableList([e[1], e[2], e[3]])), FreeModule(Expression(Integer), OrderedVariableList([g[1], g[2], g[3], g[4]])))
fricas t23:=tensor(v2,v3)$M23
Type: TensorProduct ?(Expression(Integer), OrderedVariableList([g[1], g[2], g[3], g[4]]), OrderedVariableList([h[;1], h[;2], h[;3], h[;4]]), FreeModule(Expression(Integer), OrderedVariableList([g[1], g[2], g[3], g[4]])), FreeModule(Expression(Integer), OrderedVariableList([h[;1], h[;2], h[;3], h[;4]])))
fricas t123:=tensor(t12,v3)$M123
Type: TensorProduct ?(Expression(Integer), Product( OrderedVariableList([e[1], e[2], e[3]]), OrderedVariableList([g[1], g[2], g[3], g[4]])), OrderedVariableList([h[;1], h[;2], h[;3], h[;4]]), TensorProduct ?(Expression(Integer), OrderedVariableList([e[1], e[2], e[3]]), OrderedVariableList([g[1], g[2], g[3], g[4]]), FreeModule(Expression(Integer), OrderedVariableList([e[1], e[2], e[3]])), FreeModule(Expression(Integer), OrderedVariableList([g[1], g[2], g[3], g[4]]))), FreeModule(Expression(Integer), OrderedVariableList([h[;1], h[;2], h[;3], h[;4]])))
fricas N:=TensorPower(3,R,B2,M2)
Type: Type
fricas tt3:=tensor([(g.1)::M2,(g.2)::M2,(g.4)::M2])$N
Type: TensorPower ?(3, Expression(Integer), OrderedVariableList([g[1], g[2], g[3], g[4]]), FreeModule(Expression(Integer), OrderedVariableList([g[1], g[2], g[3], g[4]])))
fricas --
construct(e.1,g.1)$Product(B1,B2)::M12
Cannot convert the value from type Product(OrderedVariableList([e[1]
,e[2],e[3]]),OrderedVariableList([g[1],g[2],g[3],g[4]])) to
TensorProduct(Expression(Integer),OrderedVariableList([e[1],e[2],
e[3]]),OrderedVariableList([g[1],g[2],g[3],g[4]]),FreeModule(
Expression(Integer),OrderedVariableList([e[1],e[2],e[3]])),
FreeModule(Expression(Integer),OrderedVariableList([g[1],g[2],g[3
],g[4]]))) .
Tensor product of three or more different spaces:
where and
. The problem can be seen in
the output of equation 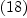 .
In order to get the output correct how should B12 be set?
|
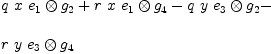
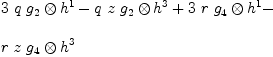
![\label{eq18}\begin{array}{@{}l}
\displaystyle
{3 \ q \ x \ {{\left[{e_{1}}, \:{g_{2}}\right]}\otimes{h^{1}}}}-{q \ x \ z \ {{\left[{e_{1}}, \:{g_{2}}\right]}\otimes{h^{3}}}}+
\
\
\displaystyle
{3 \ r \ x \ {{\left[{e_{1}}, \:{g_{4}}\right]}\otimes{h^{1}}}}-{r \ x \ z \ {{\left[{e_{1}}, \:{g_{4}}\right]}\otimes{h^{3}}}}-
\
\
\displaystyle
{3 \ q \ y \ {{\left[{e_{3}}, \:{g_{2}}\right]}\otimes{h^{1}}}}+{q \ y \ z \ {{\left[{e_{3}}, \:{g_{2}}\right]}\otimes{h^{3}}}}-
\
\
\displaystyle
{3 \ r \ y \ {{\left[{e_{3}}, \:{g_{4}}\right]}\otimes{h^{1}}}}+{r \ y \ z \ {{\left[{e_{3}}, \:{g_{4}}\right]}\otimes{h^{3}}}}
\label{eq18}\begin{array}{@{}l}
\displaystyle
{3 \ q \ x \ {{\left[{e_{1}}, \:{g_{2}}\right]}\otimes{h^{1}}}}-{q \ x \ z \ {{\left[{e_{1}}, \:{g_{2}}\right]}\otimes{h^{3}}}}+
\
\
\displaystyle
{3 \ r \ x \ {{\left[{e_{1}}, \:{g_{4}}\right]}\otimes{h^{1}}}}-{r \ x \ z \ {{\left[{e_{1}}, \:{g_{4}}\right]}\otimes{h^{3}}}}-
\
\
\displaystyle
{3 \ q \ y \ {{\left[{e_{3}}, \:{g_{2}}\right]}\otimes{h^{1}}}}+{q \ y \ z \ {{\left[{e_{3}}, \:{g_{2}}\right]}\otimes{h^{3}}}}-
\
\
\displaystyle
{3 \ r \ y \ {{\left[{e_{3}}, \:{g_{4}}\right]}\otimes{h^{1}}}}+{r \ y \ z \ {{\left[{e_{3}}, \:{g_{4}}\right]}\otimes{h^{3}}}}](images/5599188335476878363-16.0px.png)