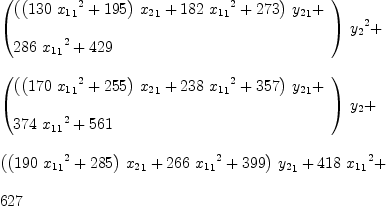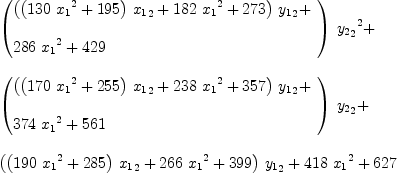http://en.wikipedia.org/wiki/Tensor_product
A tensor product is "the most general bilinear operation" available in
a specified domain of computation, satisfying:
We can use the domain constructor Sum SandBoxSum
fricas
)lib SUM
Sum is now explicitly exposed in frame initial
Sum will be automatically loaded when needed from
/var/aw/var/LatexWiki/SUM.NRLIB/SUM
First we can define some recursive operations on the polynomials
fricas
scanPoly(p,n) == _
(p=0 => 0; mapMonomial(leadingMonomial(p),n)+scanPoly(reductum p,n))
Type: Void
fricas
mapMonomial(p,n) == _
monomial(coefficient(p,degree p),scanIndex(degree(p),n))$SMP(Integer,Sum(Symbol,Symbol))
Type: Void
fricas
scanIndex(p,n) == _
(zero? p => 0$IndexedExponents(Sum(Symbol,Symbol)); _
monomial(leadingCoefficient(p), _
if n=1 then in1(leadingSupport(p))$Sum(Symbol,Symbol) _
else in2(leadingSupport(p))$Sum(Symbol,Symbol) _
)$IndexedExponents(Sum(Symbol,Symbol))+ _
scanIndex(reductum(p),n))
Type: Void
For example:
fricas
-- functions are first compiled here
--
scanPoly(x,1)
There are 1 exposed and 3 unexposed library operations named
leadingMonomial having 1 argument(s) but none was determined to
be applicable. Use HyperDoc Browse, or issue
)display op leadingMonomial
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
leadingMonomial with argument type(s)
Variable(x)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 1 exposed and 3 unexposed library operations named
leadingMonomial having 1 argument(s) but none was determined to
be applicable. Use HyperDoc Browse, or issue
)display op leadingMonomial
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
leadingMonomial with argument type(s)
Variable(x)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
injects the polynomial x in to the tensor product. So
now the full tensor product is just:
fricas
tensorPoly(p,q) == _
scanPoly(p,1)*scanPoly(q,2)
Type: Void
For example:
fricas
p:=2*x^2+3
Type: Polynomial(Integer)
fricas
q:=5*x*y+7*y+11
Type: Polynomial(Integer)
fricas
r:=tensorPoly(p,q)
fricas
Compiling function scanIndex with type (IndexedExponents(Symbol),
Integer) -> IndexedExponents(Sum(Symbol,Symbol))
fricas
Compiling function mapMonomial with type (Polynomial(Integer),
Integer) -> SparseMultivariatePolynomial(Integer,Sum(Symbol,
Symbol))
fricas
Compiling function scanPoly with type (Polynomial(Integer), Integer)
-> SparseMultivariatePolynomial(Integer,Sum(Symbol,Symbol))
fricas
Compiling function tensorPoly with type (Polynomial(Integer),
Polynomial(Integer)) -> SparseMultivariatePolynomial(Integer,Sum(
Symbol,Symbol))
Type: SparseMultivariatePolynomial
?(Integer,
Sum(Symbol,
Symbol))
fricas
monomials(r)
Type: List(SparseMultivariatePolynomial
?(Integer,
Sum(Symbol,
Symbol)))
Demonstrating the axioms (1) (2) and (3) of the tensor product:
fricas
w:= 13*y^2+17*y+19
Type: Polynomial(Integer)
fricas
test( tensorPoly(p+q,w) = (tensorPoly(p,w) + tensorPoly(q,w)) )
Type: Boolean
fricas
test( tensorPoly(p,q+w) = (tensorPoly(p,q) + tensorPoly(p,w)) )
Type: Boolean
fricas
test( tensorPoly(p,23*w) = 23*tensorPoly(p,w) )
Type: Boolean
fricas
test( tensorPoly(23*p,w) = 23*tensorPoly(p,w) )
Type: Boolean
I suppose that we could give an inductive proof that this
implementation of the tensor product of polynomials is
correct ... but for now lets take this demonstration as
reassurance.
Re-coding the interpreter functions as library package.
spad
)abbrev package TPROD TensorProduct
IE ==> IndexedExponents(VAR)
IEP ==> IndexedExponents(Sum(VAR,VAR))
SMP ==> SparseMultivariatePolynomial(R,Sum(VAR,VAR))
TensorProduct(R:Ring, VAR: OrderedSet, P:PolynomialCategory(R,IE,VAR)): with
_\_/: (P,P) -> SMP
== add
scanIndex(x:IE,n:Integer):IEP ==
zero? x => 0
monomial(leadingCoefficient(x), _
if n=1 then in1(leadingSupport(x))$Sum(VAR,VAR) _
else in2(leadingSupport(x))$Sum(VAR,VAR) _
) + scanIndex(reductum(x),n)
mapMonomial(p:P,n:Integer):SMP ==
monomial(coefficient(p,degree p),scanIndex(degree(p),n))$SMP
scanPoly(p:P,n:Integer):SMP ==
p=0 => 0
mapMonomial(leadingMonomial(p),n)+scanPoly(reductum p,n)
_\_/(p:P, q:P) : SMP == scanPoly(p,1)*scanPoly(q,2)
spad
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/6318234874982058351-25px007.spad
using old system compiler.
TPROD abbreviates package TensorProduct
------------------------------------------------------------------------
initializing NRLIB TPROD for TensorProduct
compiling into NRLIB TPROD
compiling local scanIndex : (IndexedExponents VAR,Integer) -> IndexedExponents Sum(VAR,VAR)
Time: 0.04 SEC.
compiling local mapMonomial : (P,Integer) -> SparseMultivariatePolynomial(R,Sum(VAR,VAR))
Time: 0 SEC.
compiling local scanPoly : (P,Integer) -> SparseMultivariatePolynomial(R,Sum(VAR,VAR))
Time: 0 SEC.
compiling exported \/ : (P,P) -> SparseMultivariatePolynomial(R,Sum(VAR,VAR))
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |TensorProduct| REDEFINED
;;; *** |TensorProduct| REDEFINED
Time: 0 SEC.
Warnings:
[1] scanIndex: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR (Finite)) (IF (has VAR (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR (Monoid)) (IF (has VAR (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR (AbelianMonoid)) (IF (has VAR (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR (CancellationAbelianMonoid)) (IF (has VAR (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR (Group)) (IF (has VAR (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR (AbelianGroup)) (IF (has VAR (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR (OrderedAbelianMonoidSup)) (IF (has VAR (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR (OrderedSet)) (IF (has VAR (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR) (: bcomp VAR)) $)) (SIGNATURE in1 ($ VAR)) (SIGNATURE in2 ($ VAR)))
[2] mapMonomial: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR (Finite)) (IF (has VAR (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR (Monoid)) (IF (has VAR (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR (AbelianMonoid)) (IF (has VAR (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR (CancellationAbelianMonoid)) (IF (has VAR (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR (Group)) (IF (has VAR (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR (AbelianGroup)) (IF (has VAR (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR (OrderedAbelianMonoidSup)) (IF (has VAR (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR (OrderedSet)) (IF (has VAR (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR) (: bcomp VAR)) $)) (SIGNATURE in1 ($ VAR)) (SIGNATURE in2 ($ VAR)))
[3] scanPoly: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR (Finite)) (IF (has VAR (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR (Monoid)) (IF (has VAR (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR (AbelianMonoid)) (IF (has VAR (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR (CancellationAbelianMonoid)) (IF (has VAR (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR (Group)) (IF (has VAR (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR (AbelianGroup)) (IF (has VAR (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR (OrderedAbelianMonoidSup)) (IF (has VAR (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR (OrderedSet)) (IF (has VAR (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR) (: bcomp VAR)) $)) (SIGNATURE in1 ($ VAR)) (SIGNATURE in2 ($ VAR)))
Cumulative Statistics for Constructor TensorProduct
Time: 0.04 seconds
finalizing NRLIB TPROD
Processing TensorProduct for Browser database:
--->/usr/local/lib/fricas/target/x86_64-linux-gnu/../../src/algebra/TENSOR.spad-->TensorProduct(constructor): Not documented!!!!
--->/usr/local/lib/fricas/target/x86_64-linux-gnu/../../src/algebra/TENSOR.spad-->TensorProduct((\/ ((SparseMultivariatePolynomial R (Sum VAR VAR)) P P))): Not documented!!!!
--->/usr/local/lib/fricas/target/x86_64-linux-gnu/../../src/algebra/TENSOR.spad-->TensorProduct(): Missing Description
; compiling file "/var/aw/var/LatexWiki/TPROD.NRLIB/TPROD.lsp" (written 04 APR 2022 07:17:46 PM):
; /var/aw/var/LatexWiki/TPROD.NRLIB/TPROD.fasl written
; compilation finished in 0:00:00.023
------------------------------------------------------------------------
TensorProduct is now explicitly exposed in frame initial
TensorProduct will be automatically loaded when needed from
/var/aw/var/LatexWiki/TPROD.NRLIB/TPRODfricas
test( p\/q = r )
Type: Boolean
fricas
test( (p+q) \/ w = (p\/w) + (q\/w) )
Type: Boolean
fricas
test( p \/ (q+w) = (p\/q) + (p\/w) )
Type: Boolean
fricas
test( p \/ (23*w) = 23*(p\/w) )
Type: Boolean
fricas
test( (23*p) \/ w = 23*(p\/w) )
Type: Boolean
Here's another way to write this - maybe better this way as first
step to express associativity of the tensor product.
spad
)abbrev package TPROD2 TensorProduct2
IE1 ==> IndexedExponents(VAR1)
IE2 ==> IndexedExponents(VAR2)
S ==> Sum(VAR1,VAR2)
IEP ==> IndexedExponents(S)
SMP ==> SparseMultivariatePolynomial(R,S)
TensorProduct2(R:Ring, VAR1: OrderedSet, VAR2: OrderedSet, P:PolynomialCategory(R,IE1,VAR1), Q:PolynomialCategory(R,IE2,VAR2)): with
_\_/: (P,Q) -> SMP
== add
scanIndex1(x:IE1):IEP ==
zero? x => 0
monomial(leadingCoefficient(x), in1(leadingSupport(x))$S) + scanIndex1(reductum(x))
scanIndex2(x:IE2):IEP ==
zero? x => 0
monomial(leadingCoefficient(x), in2(leadingSupport(x))$S) + scanIndex2(reductum(x))
mapMonomial1(p:P):SMP ==
monomial(coefficient(p,degree p),scanIndex1(degree(p)))$SMP
mapMonomial2(q:Q):SMP ==
monomial(coefficient(q,degree q),scanIndex2(degree(q)))$SMP
scanPoly1(p:P):SMP ==
p=0 => 0
mapMonomial1(leadingMonomial(p))+scanPoly1(reductum p)
scanPoly2(q:Q):SMP ==
q=0 => 0
mapMonomial2(leadingMonomial(q))+scanPoly2(reductum q)
_\_/(p:P, q:Q) : SMP == scanPoly1(p)*scanPoly2(q)
spad
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/4565958775469301848-25px009.spad
using old system compiler.
TPROD2 abbreviates package TensorProduct2
------------------------------------------------------------------------
initializing NRLIB TPROD2 for TensorProduct2
compiling into NRLIB TPROD2
compiling local scanIndex1 : IndexedExponents VAR1 -> IndexedExponents Sum(VAR1,VAR2)
Time: 0.02 SEC.
compiling local scanIndex2 : IndexedExponents VAR2 -> IndexedExponents Sum(VAR1,VAR2)
Time: 0 SEC.
compiling local mapMonomial1 : P -> SparseMultivariatePolynomial(R,Sum(VAR1,VAR2))
Time: 0 SEC.
compiling local mapMonomial2 : Q -> SparseMultivariatePolynomial(R,Sum(VAR1,VAR2))
Time: 0 SEC.
compiling local scanPoly1 : P -> SparseMultivariatePolynomial(R,Sum(VAR1,VAR2))
Time: 0 SEC.
compiling local scanPoly2 : Q -> SparseMultivariatePolynomial(R,Sum(VAR1,VAR2))
Time: 0 SEC.
compiling exported \/ : (P,Q) -> SparseMultivariatePolynomial(R,Sum(VAR1,VAR2))
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |TensorProduct2| REDEFINED
;;; *** |TensorProduct2| REDEFINED
Time: 0 SEC.
Warnings:
[1] scanIndex1: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR1 (Finite)) (IF (has VAR2 (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR1 (Monoid)) (IF (has VAR2 (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR1 (AbelianMonoid)) (IF (has VAR2 (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (CancellationAbelianMonoid)) (IF (has VAR2 (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (Group)) (IF (has VAR2 (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR1 (AbelianGroup)) (IF (has VAR2 (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR1 (OrderedAbelianMonoidSup)) (IF (has VAR2 (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR1 (OrderedSet)) (IF (has VAR2 (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR1) (: bcomp VAR2)) $)) (SIGNATURE in1 ($ VAR1)) (SIGNATURE in2 ($ VAR2)))
[2] mapMonomial1: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR1 (Finite)) (IF (has VAR2 (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR1 (Monoid)) (IF (has VAR2 (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR1 (AbelianMonoid)) (IF (has VAR2 (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (CancellationAbelianMonoid)) (IF (has VAR2 (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (Group)) (IF (has VAR2 (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR1 (AbelianGroup)) (IF (has VAR2 (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR1 (OrderedAbelianMonoidSup)) (IF (has VAR2 (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR1 (OrderedSet)) (IF (has VAR2 (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR1) (: bcomp VAR2)) $)) (SIGNATURE in1 ($ VAR1)) (SIGNATURE in2 ($ VAR2)))
[3] scanPoly1: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR1 (Finite)) (IF (has VAR2 (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR1 (Monoid)) (IF (has VAR2 (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR1 (AbelianMonoid)) (IF (has VAR2 (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (CancellationAbelianMonoid)) (IF (has VAR2 (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (Group)) (IF (has VAR2 (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR1 (AbelianGroup)) (IF (has VAR2 (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR1 (OrderedAbelianMonoidSup)) (IF (has VAR2 (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR1 (OrderedSet)) (IF (has VAR2 (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR1) (: bcomp VAR2)) $)) (SIGNATURE in1 ($ VAR1)) (SIGNATURE in2 ($ VAR2)))
[4] scanPoly2: not known that (OrderedSet) is of mode (CATEGORY domain (IF (has VAR1 (Finite)) (IF (has VAR2 (Finite)) (ATTRIBUTE (Finite)) noBranch) noBranch) (IF (has VAR1 (Monoid)) (IF (has VAR2 (Monoid)) (ATTRIBUTE (Monoid)) noBranch) noBranch) (IF (has VAR1 (AbelianMonoid)) (IF (has VAR2 (AbelianMonoid)) (ATTRIBUTE (AbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (CancellationAbelianMonoid)) (IF (has VAR2 (CancellationAbelianMonoid)) (ATTRIBUTE (CancellationAbelianMonoid)) noBranch) noBranch) (IF (has VAR1 (Group)) (IF (has VAR2 (Group)) (ATTRIBUTE (Group)) noBranch) noBranch) (IF (has VAR1 (AbelianGroup)) (IF (has VAR2 (AbelianGroup)) (ATTRIBUTE (AbelianGroup)) noBranch) noBranch) (IF (has VAR1 (OrderedAbelianMonoidSup)) (IF (has VAR2 (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch) noBranch) (IF (has VAR1 (OrderedSet)) (IF (has VAR2 (OrderedSet)) (ATTRIBUTE (OrderedSet)) noBranch) noBranch) (SIGNATURE selectsum ((Union (: acomp VAR1) (: bcomp VAR2)) $)) (SIGNATURE in1 ($ VAR1)) (SIGNATURE in2 ($ VAR2)))
Cumulative Statistics for Constructor TensorProduct2
Time: 0.02 seconds
finalizing NRLIB TPROD2
Processing TensorProduct2 for Browser database:
--->-->TensorProduct2(constructor): Not documented!!!!
--->-->TensorProduct2((\/ ((SparseMultivariatePolynomial R (Sum VAR1 VAR2)) P Q))): Not documented!!!!
--->-->TensorProduct2(): Missing Description
; compiling file "/var/aw/var/LatexWiki/TPROD2.NRLIB/TPROD2.lsp" (written 04 APR 2022 07:17:46 PM):
; /var/aw/var/LatexWiki/TPROD2.NRLIB/TPROD2.fasl written
; compilation finished in 0:00:00.033
------------------------------------------------------------------------
TensorProduct2 is now explicitly exposed in frame initial
TensorProduct2 will be automatically loaded when needed from
/var/aw/var/LatexWiki/TPROD2.NRLIB/TPROD2fricas
test( p\/q = r )
Type: Boolean
fricas
test( (p+q) \/ w = (p\/w) + (q\/w) )
Type: Boolean
fricas
test( p \/ (q+w) = (p\/q) + (p\/w) )
Type: Boolean
fricas
test( p \/ (23*w) = 23*(p\/w) )
Type: Boolean
fricas
test( (23*p) \/ w = 23*(p\/w) )
Type: Boolean
Associativity of the tensor product means these two expressions
should be identical:
fricas
(p\/q)\/w
Type: SparseMultivariatePolynomial
?(Integer,
Sum(Sum(Symbol,
Symbol),
Symbol))
fricas
p\/(q\/w)
Type: SparseMultivariatePolynomial
?(Integer,
Sum(Symbol,
Sum(Symbol,
Symbol)))