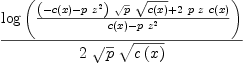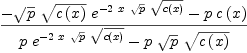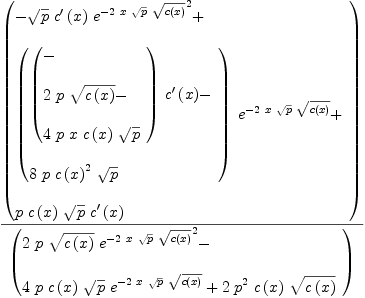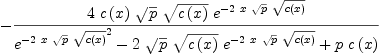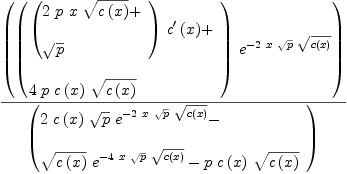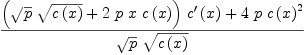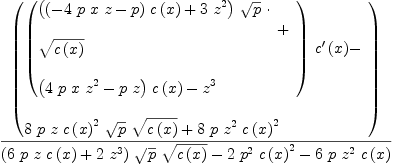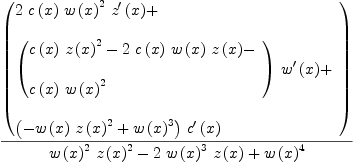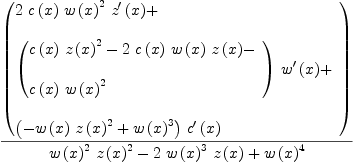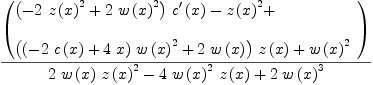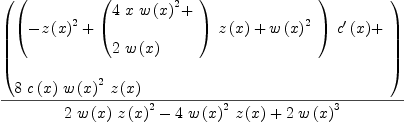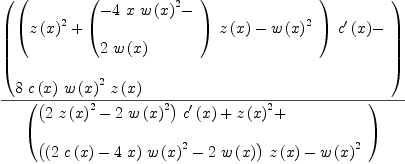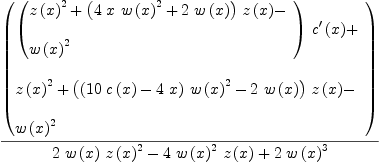Test 1: solve a simple nonlinear homogeneous differential equation fricas y := operator y
Type: BasicOperator?
fricas deq1 := D(y(x),
Type: Equation(Expression(Integer))
fricas solve(deq1,
Type: Union(Expression(Integer),
Test 2: solve a class of simple nonlinear homogeneous differential equations fricas deq2a := D(y(x),
Type: Equation(Expression(Integer))
fricas xpr2b := solve(deq2a,
Type: Union(Expression(Integer),
fricas simplify(x-xpr2b)
Type: Expression(Integer)
Test 3: find general solutions for nonlinear homogeneous differential equations fricas f := operator f
Type: BasicOperator?
fricas deq3 := D(y(x),
Type: Equation(Expression(Integer))
fricas solve(deq3,
Type: Union(Expression(Integer),
Test 4: integration fricas integrate(1/(1-x^2),
Type: Union(Expression(Integer),
Test 5: check result fricas xpr5 := (log(x+1)-log(x-1))/2
Type: Expression(Integer)
fricas D(xpr5,
Type: Expression(Integer)
Test 6: check simplification fricas xpr6 := log(1+2/(x-1))/2
Type: Expression(Integer)
fricas D(xpr6,
Type: Expression(Integer)
Test 7: Express y(x) as function of x (replacing y(x) with z) fricas eq7a := x = (log(z+1)-log(z-1))/2
Type: Equation(Expression(Integer))
fricas solve(eq7a,
Type: List(Equation(Expression(Integer)))
fricas xpr7b := (1+exp(-2*z))/(1-exp(-2*z))
Type: Expression(Integer)
fricas simplify(xpr7b)
Type: Expression(Integer)
Test 8: check simplified result fricas xpr8 := (1+exp(-2*x))/(1-exp(-2*x)) - (1+2/(exp(2*x)-1))
Type: Expression(Integer)
fricas simplify(xpr8)
Type: Expression(Integer)
Test 9: check result by substitution in the DEQ fricas xpr9a := (1+2/(exp(2*x)-1))
Type: Expression(Integer)
fricas xpr9b := D(xpr9a,
Type: Expression(Integer)
fricas xpr9c := 1 - (xpr9a)^2
Type: Expression(Integer)
Test 10: finding the explicit solution for the deq in test 2 fricas wcp := sqrt(c*p)
Type: Expression(Integer)
fricas xpr10a := log(((p*z^2+c)*wcp-2*c*p*z)/(p*z^2-c))/(2*wcp)
Type: Expression(Integer)
fricas solve(x = xpr10a,
Type: List(Equation(Expression(Integer)))
fricas eq10c := (p*z^2+c)*wcp-2*c*p*z
Type: Expression(Integer)
fricas solve(eq10c=0,
Type: List(Equation(Expression(Integer)))
fricas xpr10d := p*wcp*(z-wcp/p)^2
Type: Expression(Integer)
fricas simplify(xpr10d/eq10c)
Type: Expression(Integer)
fricas xpr10e := (wcp/p)*(2/(1-exp(-2*wcp*x)/wcp)-1)
Type: Expression(Integer)
fricas xpr10f := D(xpr10e,
Type: Expression(Integer)
fricas xpr10g := c - p*(xpr10e)^2
Type: Expression(Integer)
fricas simplify(xpr10f / xpr10g)
Type: Expression(Integer)
Test 11: non-homogeneous generalization: c as linear function of x fricas deq11a := D(y(x),
Type: Equation(Expression(Integer))
fricas solve(deq11a,
Type: Union("failed",
Test 12: non-homogeneous generalization: c as arbitrary function of x fricas c := operator c
Type: BasicOperator?
fricas deq12a := D(y(x),
Type: Equation(Expression(Integer))
fricas solve(deq12a,
Type: Union("failed",
Test 13: guessing solution for deq12a fricas wpcx := sqrt(c(x))*sqrt(p)
Type: Expression(Integer)
fricas xpr13a := log((p*wpcx*(z-wpcx/p)^2)/(p*z^2-c(x)))/(2*wpcx)
Type: Expression(Integer)
fricas xpr13b := (wpcx/p)*(2/(1-exp(-2*wpcx*x)/wpcx)-1)
Type: Expression(Integer)
fricas xpr13c := D(xpr13b,
Type: Expression(Integer)
fricas xpr13d := c(x) - p*(xpr13b)^2
Type: Expression(Integer)
fricas simplify(xpr13d / xpr13c)
Type: Expression(Integer)
fricas xpr13e := simplify(D((2/(1-exp(-2*wpcx*x)/wpcx)-1),
Type: Expression(Integer)
fricas xpr13f := (wpcx-exp(-2*wpcx*x))^2
Type: Expression(Integer)
fricas xpr13g := simplify(((2*p*c(x)*x+wpcx)*D(c(x),
Type: Expression(Integer)
fricas xpr13h := simplify((1+2*wpcx*x)*D(c(x),
Type: Expression(Integer)
fricas simplify(xpr13h/xpr13g)
Type: Expression(Integer)
fricas xpr13i := simplify((1/(wpcx-z)-1/(2*wpcx))*D(c(x),
Type: Expression(Integer)
fricas w := operator w
Type: BasicOperator?
fricas z := operator z
Type: BasicOperator?
fricas simplify(D((2/(1-z(x)/w(x))-1)*c(x)/w(x),
Type: Expression(Integer)
fricas simplify((2*c(x)*w(x)^2*D(z(x),
Type: Expression(Integer)
fricas xpr13j := simplify((2*c(x)*w(x)^2*w(x)*z(x)*(x/c(x)-1/2)+(z(x)^2-2*w(x)*z(x)-w(x)^2)*c(x)*(-w(x)/(2*c(x)))+(w(x)^3-w(x)*z(x)^2)*D(c(x),
Type: Expression(Integer)
fricas xpr13k := simplify((1/(w(x)-z(x))-1/(2*w(x)))*D(c(x),
Type: Expression(Integer)
fricas simplify(xpr13k/xpr13j)
Type: Expression(Integer)
fricas simplify(xpr13k-xpr13j)
Type: Expression(Integer)
|
|
|
|
last edited 16 years ago by jv1 |
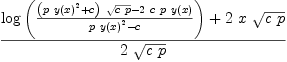
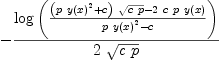
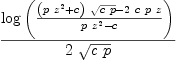
![\label{eq26}\begin{array}{@{}l}
\displaystyle
\left[{z ={{-{{\sqrt{c \ p}}\ {{{e}^{2 \ x \ {\sqrt{c \ p}}}}^{2}}}-{2 \ c \ p \ {{e}^{2 \ x \ {\sqrt{c \ p}}}}}-{c \ p \ {\sqrt{c \ p}}}}\over{{p \ {{{e}^{2 \ x \ {\sqrt{c \ p}}}}^{2}}}-{c \ {{p}^{2}}}}}}, \: \right.
\
\
\displaystyle
\left.{z ={{\sqrt{c \ p}}\over p}}\right]
\label{eq26}\begin{array}{@{}l}
\displaystyle
\left[{z ={{-{{\sqrt{c \ p}}\ {{{e}^{2 \ x \ {\sqrt{c \ p}}}}^{2}}}-{2 \ c \ p \ {{e}^{2 \ x \ {\sqrt{c \ p}}}}}-{c \ p \ {\sqrt{c \ p}}}}\over{{p \ {{{e}^{2 \ x \ {\sqrt{c \ p}}}}^{2}}}-{c \ {{p}^{2}}}}}}, \: \right.
\
\
\displaystyle
\left.{z ={{\sqrt{c \ p}}\over p}}\right]](images/3964135414081652212-16.0px.png)