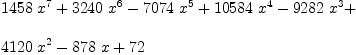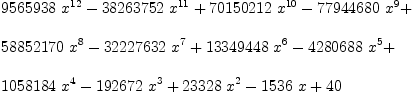MathAction UnivariatePolynomial

Topics

FrontPage
- DesignIssues
  - Where do variables belong?
    - UnivariatePolynomial <-- You are here.

Section 9.83 UnivariatePolynomial

The domain constructor UnivariatePolynomial (abbreviated UP) creates domains of univariate polynomials in a specified variable. For example, the domain UP(a1,POLY FRAC INT) provides polynomials in the single variable a1 whose coefficients are general polynomials with rational number coefficients. UP(x,INT) is the domain of polynomials in the single variable x with integer coefficients.

Example operations on univariate polynomials

axiom

(p,q) : UP(x,INT)

Type: Void

axiom

p := (3*x-1)**2 * (2*x + 8)

$\label{eq1}{{18}\ {x^3}}+{{60}\ {x^2}}-{{46}\ x}+ 8$

(1)

Type: UnivariatePolynomial(x,Integer)

axiom

q := (1 - 6*x + 9*x**2)**2

$\label{eq2}{{81}\ {x^4}}-{{108}\ {x^3}}+{{54}\ {x^2}}-{{12}\ x}+ 1$

(2)

Type: UnivariatePolynomial(x,Integer)

axiom

p**2 + p*q

$\label{eq3}\begin{array}{@{}l} \displaystyle {{1458}\ {x^7}}+{{3240}\ {x^6}}-{{7074}\ {x^5}}+{{10584}\ {x^4}}-{{9282}\ {x^3}}+ \ \ \displaystyle {{4120}\ {x^2}}-{{878}\ x}+{72}$

(3)

Type: UnivariatePolynomial(x,Integer)

axiom

D p

$\label{eq4}{{54}\ {x^2}}+{{120}\ x}-{46}$

(4)

Type: UnivariatePolynomial(x,Integer)

axiom

integrate p

$\label{eq5}{{9 \over 2}\ {x^4}}+{{20}\ {x^3}}-{{23}\ {x^2}}+{8 \ x}$

(5)

Type: UnivariatePolynomial(x,Fraction(Integer))

axiom

p 2

$\label{eq6}300$

(6)

Type: PositiveInteger

axiom

subst(p,x=2)

$\label{eq7}300$

(7)

Type: Expression(Integer)

axiom

2 p

$\label{eq8}2$

(8)

Type: UnivariatePolynomial(x,Integer)

axiom

p q

$\label{eq9}\begin{array}{@{}l} \displaystyle {{9565938}\ {x^{12}}}-{{38263752}\ {x^{11}}}+{{70150212}\ {x^{10}}}-{{77944680}\ {x^9}}+ \ \ \displaystyle {{58852170}\ {x^8}}-{{32227632}\ {x^7}}+{{13349448}\ {x^6}}-{{4 280688}\ {x^5}}+ \ \ \displaystyle {{1058184}\ {x^4}}-{{192672}\ {x^3}}+{{23328}\ {x^2}}-{{1536}\ x}+{40}$

(9)

Type: UnivariatePolynomial(x,Integer)

axiom

q p

$\label{eq10}\begin{array}{@{}l} \displaystyle {{8503056}\ {x^{12}}}+{{113374080}\ {x^{11}}}+{{479950272}\ {x^{10}}}+ \ \ \displaystyle {{404997408}\ {x^9}}-{{1369516896}\ {x^8}}-{{626146848}\ {x^7}}+ \ \ \displaystyle {{2939858712}\ {x^6}}-{{2780728704}\ {x^5}}+{{1364312160}\ {x^4}}- \ \ \displaystyle {{396838872}\ {x^3}}+{{69205896}\ {x^2}}-{{6716184}\ x}+{279 841}$

(10)

Type: UnivariatePolynomial(x,Integer)

axiom

y:Symbol

Type: Void

axiom

1 y

$\label{eq11}1$

(11)

Type: UnivariatePolynomial(y,Integer)

axiom

$\label{eq12}w$

(12)

Type: Variable(w)

axiom

p w

$\label{eq13}{{18}\ {w^3}}+{{60}\ {w^2}}-{{46}\ w}+ 8$

(13)

Type: Fraction(Polynomial(Integer))

axiom

vectorise(p,5)

$\label{eq14}\left[ 8, \: -{46}, \:{60}, \:{18}, \: 0 \right]$

(14)

Type: Vector(Integer)

axiom

t : UP(a1,FRAC POLY INT)

Type: Void

axiom

t := a1**2 - a1/b2 + (b1**2-b1)/(b2+3)

$\label{eq15}{a 1^2}-{{1 \over b 2}\ a 1}+{{{b 1^2}- b 1}\over{b 2 + 3}}$

(15)

Type: UnivariatePolynomial(a1,Fraction(Polynomial(Integer)))

axiom

u : FRAC POLY INT := t

$\label{eq16}{{{a 1^2}\ {b 2^2}}+{{\left({b 1^2}- b 1 +{3 \ {a 1^2}}- a 1 \right)}\ b 2}-{3 \ a 1}}\over{{b 2^2}+{3 \ b 2}}$

(16)

Type: Fraction(Polynomial(Integer))

axiom

u :: UP(b1,?)

$\label{eq17}{{1 \over{b 2 + 3}}\ {b 1^2}}-{{1 \over{b 2 + 3}}\ b 1}+{{{{a 1^2}\ b 2}- a 1}\over b 2}$

(17)

Type: UnivariatePolynomial(b1,Fraction(Polynomial(Integer)))

Subject: Be Bold !!

	( 7 subscribers )