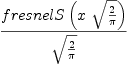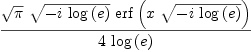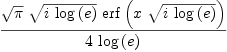Axiom doesn't seem to do the integral of sin(x^2), but both Maxima and Mathematica (per http://integrals.wolfram.com/ anyway) produce answers. Confirmed by Martin Rubey, and uploaded at his request to IssueTracker.

CY

integrate(sin(x**2),x)

(1)

However:

 Maxima 5.9.1.1cvs http://maxima.sourceforge.net
 Using Lisp CMU Common Lisp 19b (19B)
 Distributed under the GNU Public License. See the file COPYING.
 Dedicated to the memory of William Schelter.
 This is a development version of Maxima. The function bug_report()
 provides bug reporting information.
 (%i1) integrate(sin(x**2),x);
                                             (sqrt(2) %i + sqrt(2)) x
 (%o1) sqrt(%pi) ((sqrt(2) %i + sqrt(2)) erf(------------------------)
                                                        2
                                     (sqrt(2) %i - sqrt(2)) x
        + (sqrt(2) %i - sqrt(2)) erf(------------------------))/8
                                                2
 (%i2)

It's worth noting that both Maple and Mathematica produce the FresnelS? function, which is defined in terms of this integral. However, the Maxima answer appears to be correct as well.

Note that is a D-finite function:

f := sin(x^2)

(2)

4*x^3*f - D(f,x) + x*D(f,x,2)

(3)

Thus integration should be "easy"...

I browsed the web a little more and came to the conclusion that the Risch algorithm only deals with elementary functions whose integral is elementary, too. "Clearly" (looking at maxima's output or browsing the web), does not have an elementary antiderivative. Hence, I suspect that it should be treated just as , by the PatternMatchIntegration package. This would not be too difficult, probably.

Martin

Although this does not really solve the original problem, I think I found a bug in INTPM. Currently, there is an operation:

           pmComplexintegrate(f, x) ==
             (rc := splitConstant(f, x)).const ^= 1 =>
               (u := pmintegrate(rc.nconst, x)) case "failed" => "failed"
               rec := u::ANS
               [rc.const * rec.special, rc.const * rec.integrand]
             cse := (rec := matcherfei(f, x, true)).which
             cse = ERF  => [rec.coeff * erf(rec.exponent), 0]
             "failed"

It is pretty obvious that the third line should read:

               (u := pmComplexintegrate(rc.nconst, x)) case "failed" => "failed"

instead. If we perform this change, we get instead of

complexIntegrate(-%i/2*e^(%i*x^2),x)

(4)

the correct answer, same for

complexIntegrate(%i/2*e^(-%i*x^2),x)

(5)

For some reason, it still won't do

complexIntegrate(sin(x^2),x)

(6)

Curiously, the pattern matcher is not even invoked in this case... Even if we enter the integral as

complexIntegrate(-%i/2*e^(%i*x^2)+%i/2*e^(-%i*x^2),x)

(7)

it fails, although in this case the pattern matcher is invoked. It would need to be invoked on each summand seperately, though.

Martin

There is another issue I don't quite understand. Currently axiom returns the whole integral unevaluated if it does not manage to evaluate it completely. If it were not for the bug #199, the following were an example:

integrate(exp(x)/x+exp(-x^2)+1/log(x),x)

(8)

Although axiom produces the intermediate result integrate(exp(x)/x+exp(-x^2),x)+li(x), it discards it. The responsible line of code is in rinteg$FSINT :

    rinteg(i, f, x, h, comp) ==
      not elem? i => integral(f, x)$F
      empty? rest(l := [mkPrimh(f, x, h, comp) for f in expand i]) => first l
      l

Does this make sense?

Martin

partially fixed in FriCAS