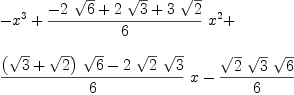I just ran across the following astonishing bug: fricas s :=-x^3+1/6*(-2*sqrt(6)+2*sqrt(3)+3*sqrt(2))*x^2+1/6*((sqrt(3)+sqrt(2))*sqrt(6)-2*sqrt(2)*sqrt(3))*x-sqrt(2)*sqrt(3)*sqrt(6)/6
Type: Polynomial(AlgebraicNumber?)
fricas factor s
Type: Factored(Polynomial(AlgebraicNumber?))
This is the same problem as 191ExquoAndThereforeGcdCannotHandleUPXEXPRINT. Namely, the roots sqrt(2), sqrt(3) and sqrt(6) are dependent, which cause problems because sqrt(6)^2 = 6 = 23 = sqrt(2)^2sqrt(3)^2 but we do not know if sqrt(6) = sqrt(2)sqrt(3) or sqrt(6) = -sqrt(2)sqrt(3). This effectively creates ring with zero divisors, while factoring/GCD routines assume a field. There are several things to notice, in fact:
Martin ... --kratt6, Wed, 25 Jan 2006 04:50:05 -0600 reply In fact, the problem shows already with
fricas s :=x^2-sqrt(2)*sqrt(3)*sqrt(6)
Type: Polynomial(AlgebraicNumber?)
and it seems to occur in 'InnerAlgFactor?':
\begin{axiom}
)tr InnerAlgFactor )ma
factor(s)
\end{axiom}
Status: open => duplicate
|
|
|
|
last edited 8 years ago by test1 |