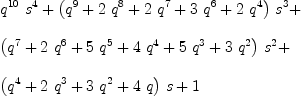The following is a very surprising for a novice, and a bit surprising for me:
fricas
c 0==1; c 1==1; c n==c(n-1)+s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..n-1]));
Type: Void
fricas
c 5
fricas
Compiling function c with type Integer -> Fraction(Polynomial(
Integer))Type: Fraction(Polynomial(Integer))
Note that the type of c 5 is FRAC POLY INT. This is, because Axiom is not smart enough to realize inside the loop that 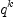 is a polynomial if
is a polynomial if 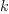 is nonnegative. The following is more surprising, though:
is nonnegative. The following is more surprising, though:
fricas
coefficient(univariate(c(5),s),3)
Type: Fraction(Polynomial(Integer))
Axiom manages - after a lot of trying- to coerce univariate(c(5),s) to a SUP FRAC POLY INT. Wow.
fricas
[coefficient(univariate(c(n),s),1) for n in 0..4]
There are 8 exposed and 6 unexposed library operations named
coefficient having 2 argument(s) but none was determined to be
applicable. Use HyperDoc Browse, or issue
)display op coefficient
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
coefficient with argument type(s)
Fraction(SparseUnivariatePolynomial(Fraction(Polynomial(Integer))))
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are 8 exposed and 6 unexposed library operations named
coefficient having 2 argument(s) but none was determined to be
applicable. Use HyperDoc Browse, or issue
)display op coefficient
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
coefficient with argument type(s)
Fraction(SparseUnivariatePolynomial(Fraction(Polynomial(Integer))))
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
But why does it give up here?
Martin
univariate applied to rational function produces rational function. Given actual
value Axiom/FriCAS can see that rational function is a polynomial and retract it.
But in a loop FriCAS has only expression producing rational functions and can
not predict that the result will be a polynomial.
fricas
Zq:=SUP(INT)
Type: Type
fricas
q:Zq := monomial(1,1)
Compiled code for c has been cleared.
Type: SparseUnivariatePolynomial
?(Integer)
fricas
Zqs:=SUP(Zq)
Type: Type
fricas
s:Zqs := monomial(1$Zq,1)
Type: SparseUnivariatePolynomial
?(SparseUnivariatePolynomial
?(Integer))
fricas
macro mac(n) == c(n-1) + s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..n-1]))
Type: Void
fricas
c(n: Integer): Zqs == (n=0 or n=1 => 1; mac n)
Function declaration c : Integer -> SparseUnivariatePolynomial(
SparseUnivariatePolynomial(Integer)) has been added to workspace.
1 old definition(s) deleted for function or rule c
Type: Void
fricas
c 0
fricas
Compiling function c with type Integer -> SparseUnivariatePolynomial
(SparseUnivariatePolynomial(Integer))Type: SparseUnivariatePolynomial
?(SparseUnivariatePolynomial
?(Integer))
fricas
c 1
Type: SparseUnivariatePolynomial
?(SparseUnivariatePolynomial
?(Integer))
fricas
c 2
Type: SparseUnivariatePolynomial
?(SparseUnivariatePolynomial
?(Integer))
fricas
mac 2
Type: SparseUnivariatePolynomial
?(SparseUnivariatePolynomial
?(Integer))
I don't know but the output of c(2) is wrong. I would have expected "? ? + 1" in accordance to mac(2).
So the typed form of you example doesn't work. And the output looks ugly anyway. :-(
Ralf
In your function you are using the
- operation for the upper bound, it is not defined for NNI or PI. Axiom is smart enough to detect the types of the step and the bounds. Because of that it is assumed that the result of (n-1) is an Integer.
Here I even don't define the type of the function:
fricas
)clear all
All user variables and function definitions have been cleared.
c 0==1; c 1==1; c n==c(n-1)+s*(reduce(+,[q^k*c(k)*c(n-1-k) for k in 1..(n-1)::NNI]));
Type: Void
fricas
[coefficient(univariate(c(n),s),1) for n in 0..4]
fricas
Compiling function c with type Integer -> Polynomial(Integer)
Type: List(Polynomial(Integer))
I don't know why it gives up in your exemple though.
Greg