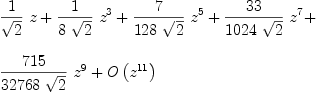Consider fricas ex := ((-((-z*z)+1)^(1/2))+1)^(1/2)
Type: Expression(Integer)
which is certainly continuous, but not differentiable at zero. Still, axiom gives fricas m:=z::UTS(AN,
fricas ((-((-m*m)+1)^(1/2))+1)^(1/2)
which is correct for positive values, but not for negative values of z. Of course, there are simpler functions that are developed like that, abs for example. Notation x = y^(1/2) really means that x^2 = y with some rule to choose which solution is desired. In UTS equation ex^2 = (1 - (1 - z)^(1/2)) has two solutions. FriCAS provides one of them. Frequently used rule is take positive square root, but this rule produces singularity (discontinuity of derivative) by jumping from one branch to the other at 0. So in many context one requires smooth roots and above we get such a root. I'm not sure what's the correct way to deal with this. MuPAD? is very careful here:
>> ex := ((-((-z*z)+1)^(1/2))+1)^(1/2)
ex := ((-((-z*z)+1)^(1/2))+1)^(1/2)
2 1/2 1/2
(1 - (1 - z ) )
>> series(ex, z=0, 5)
series(ex, z=0, 5)
/ 2 \1/2 / 2 \1/2 / 2 \1/2
2 | z | 4 | z | 6 | z |
/ 2 \1/2 z | -- | 7 z | -- | 33 z | -- |
| z | \ 2 / \ 2 / \ 2 / 8
| -- | + ------------ + -------------- + --------------- + O(z )
\ 2 / 8 128 1024
>> series(abs(z), z=0, 5)
series(abs(z), z=0, 5)
z 6
------- + O(z )
sign(z)
|
|
|
|
last edited 9 years ago by test1 |